例谈“先行组织者”教学方式及其成效

● (象山县教育局教科研中心 浙江象山 315700)

例谈“先行组织者”教学方式及其成效

●邬云德(象山县教育局教科研中心 浙江象山 315700)

1 引言

数学教育在改革与反思中形成了“过程”哲学观——“过程”(概念的形成过程、原理的发现与推导过程、解法或证法的思考过程、问题解决后的反思过程等)是数学课程内容的一部分，特别是思维方法和思想方法的展开过程是数学的重要内容．但大量课堂观察发现：目前课堂教学普遍存在“过程”短暂甚至缺失的问题．鉴于此，笔者以宁波市特级教师跨区域带徒活动为载体，采用研究性变革实践的方式，对如何解决课堂教学中普遍存在的“过程”短暂问题进行了探索．初步的理论求证与实践验证表明，探索中形成的“先行组织者”教学方式对解决“过程”短暂问题具有积极的作用．

2 “先行组织者”的概念及其形式

“先行组织者”是指教师根据数学发展规律(数学的发现、数学的完善、数学的应用)、学生学习数学的认知规律(具体到抽象、特殊到一般、现象到本质)和教育的规律(在活动中体会思维方法和思想方法以及在活动中发展能力和个性)，对教材内容进行有目的、有意识地加工、提炼，以文字、符号、图像或图表等形式表述，用于学生课前预习的含有学习新知识所需要的“生长点”(这个“生长点”不仅包括已有的知识、技能，还包括识别、联系、比较、建构等学习方法和能力)，且能对学习新知识起指导与定向作用的引导性材料(这个引导性材料与当前所学新内容之间在包容性、概括性和抽象性等方面符合认知同化理论要求)．

其基本形式有3种：(1)“先行组织者”与当前所学的新内容之间的联系方式是“类属关系”，其学习的形式类型是下位学习，其思维的形式类型是演绎；(2)“先行组织者”与当前所学新内容之间的联系方式是“总括关系”，其学习的形式类型是上位学习，其思维的形式类型是归纳；(3)“先行组织者”与当前所学新内容之间的联系方式是“并列结合关系”，其学习的形式类型是并列结合学习，其思维的形式类型是类比．

3 “先行组织者”教学方式举例

借助“先行组织者”进行教学的基本过程是：先让学生课前预习教师提供的“先行组织者”，再在课始阶段组织学生交互反馈，并在此基础上展开进一步的教学活动．本文以浙教版义务教育课程标准实验教科书《数学》7年级下册第2.4节“旋转变换”为例，说明“先行组织者”教学方式．

3.1 第1阶段：“先行组织者”引导下的预习基础上的交互反馈——“有向开放”以促进学生“资源生成”

第1步：课前预习——自主探索

课前，教师设计如下的“先行组织者”，并提前1天将其交给学生(有条件的可以借助网络平台).在独立思考基础上，要求各学习“小团体”负责人组织有关成员进行合作研讨．必要时，教师对学习“小团体”负责人作适当的培训．

(1)先指出图1～6中图形的运动特点(从△ABC到△A′B′C′)，再按运动特点将其分类．

图1

图2

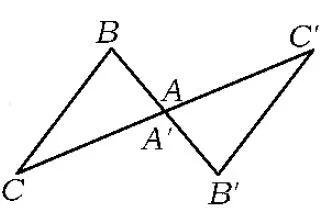
图3

图4

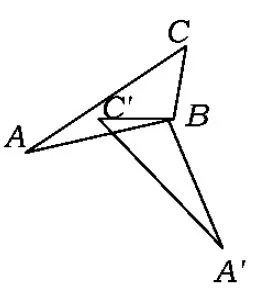
图5

图6

(2)生活中有类似于图3、图5的运动现象吗？如果有，请你举出尽可能多的生活实例.

(3)通过上述观察、分类、举例的过程，你对类似于图3、图5的这类运动现象有何感触？

提示：它与生活中相应物体的旋转运动有何关系？它与轴对称变换、平移变换的异同点是什么？类比轴对称变换、平移变换阐述研究这类图形运动的生活意义和数学意义.

第2步：汇报交流——交互反馈

上课开始，教师出示课前布置的问题，并要求学生汇报预习成果．同时教师倾听学生的汇报、交流，必要时，教师进行追问、激励、评析．在此基础上教师进行总结：

(1)图1与图4，图形的运动特点是翻折(运动前后的2个图形关于某条直线成轴对称)；图2与图6，图形的运动特点是定向移动(运动前后的2个图形的对应点连线平行)；图3与图5，图形的运动特点是绕定点旋转(运动前后的2个图形的对应点旋转相同的角度)．

(2)生活中随处可见类似于图3、图5的运动现象，如“电风扇叶片的转动”、“钟表分针的转动”、“螺旋桨叶片的转动”、“钟摆的转动”等．

(3)它是相应物体旋转运动的数学抽象．它与轴对称变换、平移变换的相同点是：它们运动前后的2个图形的形状、大小都不变.不同点是：它们运动的特征不同，它们运动前后2个图形的方向不同．研究这类图形运动的生活意义：用旋转思想方法(将局部的图形变成整体的图形)能设计和解决有关实际问题；数学意义：用旋转思想方法(将分散的图形集中起来，将分散的条件联系起来)能解决有关几何问题．

3.2 第2阶段：挑战性问题引导下的合作研讨基础上的综合概括——“互动生成”以发展学生“智慧技能”

第3步：引导探究——合作研讨

正因为这样的图形改变有丰富的现实情景和广泛的应用价值，就决定了从数学角度研究这样的图形改变的必要性．这节课的研究对象就是这样的图形改变．

接着，教师依次提出以下3个挑战性的问题，要求学生合作研讨并发表自己的观点．

问题1 如图3、图5，这样的图形改变的本质特征是什么？你是怎样发现的？如果回答这个问题有困难，请先思考：(1)图形是由点组成的，图形运动能否看成是图形上点的运动？(2)考察点的运动特征有哪些策略？

学生独立学习，教师巡视指导，约2分钟后进行交流、评析．

图7

问题2怎样确定图形改变后的新图形？如图7，O是△ABC外的一点，如何作出△ABC绕定点O按逆时针方向旋转60°后的图形？

学生独立学习，教师巡视指导，约2分钟后进行交流、示范．

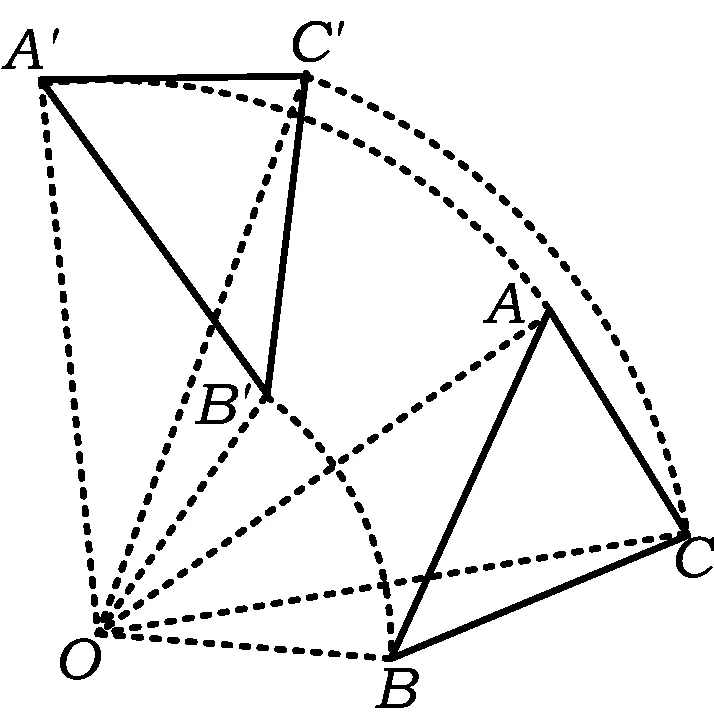
图8

问题3(1)分别指出图3、图5和图8改变前后2个图形的对应点、对应边、对应角？(2)问：改变前后2个图形有哪些不变关系？

(提示：可从整体和局部多个视角进行观察.)

学生独立学习，教师巡视指导，约3分钟后进行交流、评析．

第4步：建构理论——综合概括

在此基础上，教师引导学生概括得出旋转变换的概念、确定旋转变换后像的方法、旋转变换的性质、旋转变换蕴涵的思维方法和思想方法及3种几何变换的异同．

(1)旋转变换的概念：由一个图形改变为另一个图形，在改变的过程中，原图形上的所有点都绕一个固定的点、按同一个方向转动同一个角度，这样的图形改变叫做图形的旋转变换，简称旋转．这个固定点叫做旋转中心，旋转的角度叫做旋转角，经变换所得的新图形叫做原图形的像．

(2)确定旋转变换后像的方法：①操作法——图形整体旋转(依据是旋转的含义)．这种方法的优点：直观；缺点：操作不方便．②作图法——图形旋转化归为点旋转(依据是旋转的特征)．这种方法的优点：操作方便,更有“数学味”；缺点：抽象．这2种思想方法都有应用价值，不可偏废．

(3)旋转变换的性质：旋转变换不改变图形的形状和大小——旋转前后2个图形的对应边相等、对应角相等；对应点到旋转中心的距离相等；对应点与旋转中心连线所成的角度等于旋转的角度．旋转变换前后2个图形的不变关系是进一步认识几何的理论基础．

(4)旋转变换蕴涵的思维方法和思想方法：①思维方法——一般到特殊(图形运动→点运动→特殊点运动)和特殊到一般(特殊点运动→点运动→图形运动)；②思想方法——通过图形旋转运动将局部的图形变成整体的图形，将分散的图形集中起来，将分散的条件相互沟通．这些思维方法和思想方法具有广泛的应用价值．

3.3 第3阶段：有代表性问题引导下的合作解决基础上的反思拓展——“尝试运用”以发展学生“智慧技能”

教师在综合概括的基础上，依次提出下列4个有代表性的问题，要求学生在独立学习的基础上交流合作．

问题1 概念辨别

下面4个选项中，正确表示将正方形X绕点O按顺时针方向旋转60°的是哪一个？为什么？

A. B. C. D.

学生选择与分析，必要时，教师进行追问、评析．

问题2具体概念

(1)如图9，经过怎样的旋转变换，可由射线OP得到射线OQ？

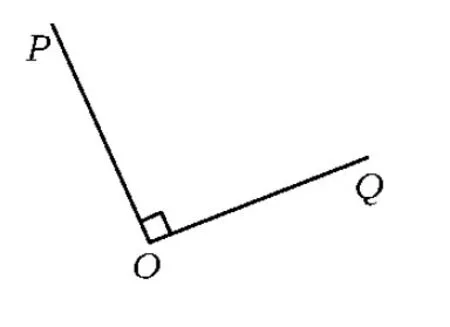
图9

图10

(2)图10是一双手的图片．能否经过一定的旋转变换，使左手的图形与右手的图形重合？经过轴对称变换呢？从中可以得到什么结论？

学生口述，必要时，教师进行追问、评析．

2018年11月13日，银隆官方称公司大股东、原董事长魏银仓侵占公司超10亿元资产，公司已就此向法院起诉，对于涉嫌犯罪的情况，公司已报案并得到珠海市公安局经侦支队的受理。

问题3方法演示

如图11，以点O为旋转中心，将线段AB按顺时针方向旋转60°，作出经过旋转变换后所得的像．请你提供尽可能多的方法，并求出像与线段AB所成的锐角度数．

学生作图操作，教师巡视指导，约2分钟后进行交流、评析．

图11

图12

问题4问题解决

图12是一个直角三角形的苗圃，由正方形花坛和2块直角三角形的草皮组成.如果2个直角三角形的2条斜边长分别为3 m和6 m，你能求出草皮的面积是多少吗？

学生独立学习，教师巡视指导，约2分钟后进行交流、评析．

第6步：做后思考——反思拓展

教师在学生解答有代表性问题的基础上，依次提出以下2个反思性问题，要求学生合作研讨并发表自己的观点．

问题5上述问题3，作图的策略(思想)是什么？用的是什么方法？具体使用了哪些技巧？一般地，旋转变换前后2个图形对应边所在直线的夹角与旋转角有何关系？

问题6上述问题4，解题的策略(思想)是什么？用的是什么方法？具体使用了哪些技巧？一般地，用旋转变换的思想方法解题的条件是什么？

教师在学生充分发表意见的基础上给出问题的答案：

(1)上述问题3作图的策略是用图形旋转的特征，用作图工具作图的方法，使用的技巧是：①先将点A,B绕定点O按顺时针方向旋转60°得点A′,B′，再联结A′B′；②过点O作线段AB所在直线的垂线，设垂足为N，然后将点N绕定点O按顺时针方向旋转60°得点N′，再过点N′作ON′的垂线，并在垂线上取N′A′=NA,N′B′=NB．一般地，旋转变换前后2个图形对应边所在直线的夹角等于旋转角或等于周角减去旋转角．

(2)上述问题4解题的策略是用图形旋转的思想，用的方法是将△BEC绕点B按逆时针方向旋转90°，使用的技巧是：先将△BEC绕点B按逆时针方向旋转90°，使分散的2个三角形变成一个大的直角三角形，再用三角形面积公式求此三角形的面积．一般地，问题涉及等腰三角形、等边三角形、等腰直角三角形、正方形时，可考虑用旋转变换的思想方法．

3.4 第4阶段：“问题清单”引导下的交流合作基础上的归纳总结——“开放延伸”以实现“拓展生成”

第7步：回顾思考——交流合作

教师在解题后反思的基础上，列出“问题清单”，鼓励学生围绕问题进行交流合作．

(1)旋转变换有何特征？旋转变换有何性质？描述旋转变换有几种方法？

(2)确定旋转变换后所得的像有几种方法？其优点、缺点分别是什么？

(3)旋转变换与轴对称变换、平移变换的相同点是什么？不同点是什么？

(4)学习旋转变换有何意义(生活意义、数学意义、对人的发展意义)？

(5)你在学习过程中，感受到了哪些思维方法和思想方法？

(6)你在学习过程中，获得了哪些数学活动的经验？碰到了哪些困难？

第8步：归纳总结——课后欣赏

教师在倾听学生交互反馈后，让学生欣赏旋转变换的自述(这部分内容可以移至课后)：即前面7步的总结(略).

4 “先行组织者”教学方式的成效

初步的理论求证与实践验证表明，“先行组织者”教学方式有以下一些成效．

(1)学生的学习效能会明显提高．首先，建立“小团体”学生的团队意识和集体荣誉感会明显增强；其次，在课前“兵教兵”的过程中，好的学生在教的过程中发展会更好，差的学生通过指导也会有所提高；第三，建立“小团体”能实现学生之间的相互监督，自我约束力会明显增强；第四，在课内分工合作的过程中合作意识和学习效率会明显提高；第五，在“大团体”交流中，“小团体”成员的积极性会明显提高．

(2)预习“先行组织者”对“过程”展开能起关键性的作用．它不但具有“整合”或重组新知识的作用，而且可以充当由已知通向未知的桥梁——不但能为整堂课的展开指明方向，而且能为整堂课的展开提供一种脚手架；它不但能为学习新知识提供先备条件，使不同层次的学生在学习新知识之前达到学习新知识所需要的大致统一的知识水平，而且能使学生注意到新、旧知识之间的内在联系；它是支撑和激励学生学习的源泉，是促使学生“自主”学习的切入点，是开启学生思维“闸门”的动力，是实现教学过程中“互动”的起因，是学生实现创新的基础，是“资源生成”的条件．

(3)预习“先行组织者”对消除“过程”短暂的现象有积极的作用．首先，课前预习提供了学生有深度思维所需要的学习条件——安静的环境和充足的时间，这给“过程”阶段快速打开理性思维的“闸门”提供了思维铺垫，从而可以加快“过程”阶段的教学节奏；其次，课前预习解决了本来在课内需要解决的部分问题，这又给“过程”阶段提供了时间保障．这能解决经历“过程”教学节奏缓慢对按时完成教学任务带来挑战的矛盾．

(4)预习“先行组织者”使数学学习成为学生的一种期待成为可能．学生对体育课、音乐课、信息技术课及各种活动课有较高的心理期望，但对抽象枯燥的数学课感兴趣的不多，原因是传统的课堂气氛沉闷，让学生表现自我的机会少．而学生通过课前在教师指导下的“备战”，从精神上、心理上、智力上作好了学习新知识的准备，并通过经历感知、分析、判断、想象和归纳等心智活动的过程，可能会产生个性化的想法，使得学生课内在教师指挥下的“作战”过程中，有表现自我的欲望，再加上教师在课内搭建了交流合作和小组竞争学习的平台，使得数学学习成为学生的一种期待成为可能．

(5)“先行组织者”教学方式体现了以“过程”为核心的教育思想．它既不一味支持建构主义理论，也不一味反对行为主义理论，而是根据不同的教学目标、具体的学习内容和不同地域及不同类别的学生实际，吸纳各种理论的合理成分作为教学的指导思想，并以数学知识发生发展过程为载体的学生认知过程和以学生为主体的数学活动过程作为教学的基本过程、以课内外结合和教师价值引导与学生自主建构相结合作为教学的基本方法、以行为过程中的“四练”(“先行组织者”引导下的具体活动、挑战性问题引导下的合作研讨、有代表性问题引导下的尝试运用、“问题清单”引导下的回顾与思考)作为教学的基本手段．这种集东西方优秀文化于一炉的教学方式，体现了过程哲学家怀特海提出的“过程”教育思想，能满足学生和谐发展的需要．

[1] 吴亚萍．“新基础教育”数学教学改革指导纲要[M]．桂林：广西师范大学出版社，2009.

[2] 顾泠沅．寻找中间地带[M]．上海：上海教育出版社，2003.

[3] 杨骞,陈金萍．论数学教学耦动理论的建构——兼谈数学教学研究的教育学取向[J]．数学教育学报，2004(4):20-23.