也谈直角三角形内有关内切圆半径的有趣结论

● (沙坡头区宣和镇洪学校 夏中卫 755006)

也谈直角三角形内有关内切圆半径的有趣结论

●张宁(沙坡头区宣和镇张洪学校 宁夏中卫 755006)

文献[1]给出了直角三角形内有关内切圆半径的几个有趣结论，本文再给出几个有趣结论．

图1

定理在Rt△ABC中，CD为斜边AB上的高．⊙I,⊙I1,⊙I2分别为△ABC,△ACD,△BCD的内切圆，其半径分别为r,r1,r2.在△II1I2中，设I1I2=d，I2I=d1，I1I=d2，设△II1I2的外接圆半径为R△II1I2，则

(1)

(2)

(3)R△II1I2=r；

(3)

(4)

(5)

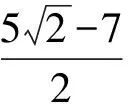
(6)

在Rt△I1DI2中，

设⊙I,⊙I1分别切AC于点E,F，联结IE,I1F,过点I1作I1G⊥IE，垂足为G，则在Rt△IGI1中，

同理可得

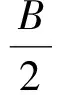
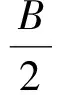
2r2+2r2(2-cosA-cosB)=

式(2)得证.

在△II1I2中，易知

由正弦定理可知

因此

式(3)得证．

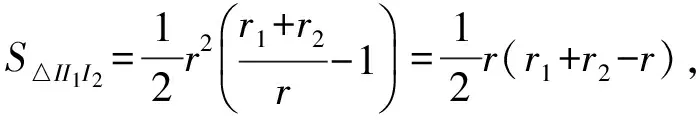
式(4)得证.

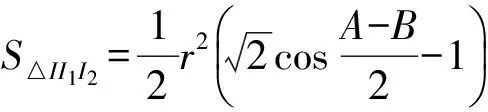
由(a-b)2≥0，知

a2+b2≥2ab，

从而

(a2+b2)+(a2+b2)≥2ab+(a2+b2)，

即

2(a2+b2)≥(a+b)2，

因此

在Rt△ABC中，a2+b2=c2，从而

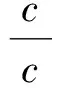
即

从而

S△ABC=r2+2Rr.

又

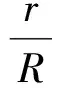
即

式(6)得证.

[1] 蔡祖才.直角三角形内有关内切圆半径的有趣结论[J].数学通讯：下半月，2010(5)：40.

《数学教育学报》2013年征订启事

《数学教育学报》是中国联合国教科文组织指导刊物，王梓坤院士任主编，全国80多家董事单位集资办刊，天津师大、中国教育学会为主办单位，北京师大、华东师大、东北师大、贵州师大、南京师大、西南大学、扬州大学、浙江师大、首都师大、湖南师大、华南师大、广州大学、江苏师大等13所高校为协办单位，是目前国内数学教育领域最高层次的学术性刊物．《学报》现为“全国中文核心期刊”、“中国科技核心期刊”和“RCCSE中国核心学术期刊(A)”．被中国科技论文统计源期刊、中国学术期刊综合评价数据库、中国学术期刊(光盘版)、中国期刊网、中国数学文摘、中国数学文献数据库、美国《数学评论》(MR)、德国《数学文摘》(ZBI)、中国人民大学报刊复印资料收录．

《学报》宗旨：服务于中小学数学教育改革及高等数学课程改革，倡导数学教育科学学术争鸣与评论，推动国内外数学教育学术交流，建构中国数学教育理论，反映国内外数学教育实践与改革的新成果，发挥对我国数学教育研究与实践的指导作用．

主要栏目：数学教育概论、争鸣与评论、现代教育技术与数学教学、调查与实验、比较数学教育、数学教育改革以及不定期开设密切贴近数学教育改革实践的专栏．

《学报》倾力将用得上的先进理论，可借鉴的国内外数学教育改革经验，带有启迪性的学术争鸣，中小学数学教改的丰硕成果，前瞻性的中小学及高等数学教育改革理念与实证性研究结论奉献给有志于数学教育事业的广大中小学、大学数学教师数学教育科研工作者．

《数学教育学报》为双月刊，104页，大16开，全年订价60元,邮局邮发代号：6-132.

欢迎有志于数学教育科研及数学教改的广大中小学数学教师、高等院校从事数学教育教学、科研及理论工作者到当地邮局订阅或向编辑部邮购．欢迎新老读者踊跃投稿．

邮购地址：天津市西青区宾水西道延长线393号 天津师范大学129信箱 《数学教育学报》编辑部

邮政编码：300387 电 话：022-23766679 E-mail：sxjyxbbjb@163.com