光学衍射图像的计算机模拟

2012-11-20张兴坊

枣庄学院学报 2012年5期

张兴坊

(枣庄学院光电工程学院，山东枣庄 277160)

0 引言

光绕过障碍物而继续传播的现象称为光的衍射，其内容是基础光学的重要组成部分［1］，其演示实验也是物理实验中常做的基础实验之一.当衍射实验选用单色性能优良的激光器作为光源时，其衍射现象又被称为夫琅禾费衍射.按照衍射屏的不同，夫琅禾费衍射主要分为单缝和圆孔衍射两种.一般只要把激光照射到衍射屏上，即可在观察屏上看到明显的衍射图样.夫琅禾费衍射实验虽然简单易做，但实验中所用的光源波长、衍射屏形状相对单一，并且衍射光斑有时肉眼分辨不清，不能及时的反映衍射图样与光源波长、屏尺寸及形貌的关系，故还需借助计算机对衍射图样进行模拟［2］，以达到对衍射现象的直观理解.本文通过分析衍射理论，利用MATLAB程序，模拟了圆孔、矩孔的夫琅禾费衍射图像，对比了不同波长的衍射光斑和孔参数的关系.

1 夫琅禾费衍射原理

光是电磁波中可见的部分，其产生衍射图样的理论基础为惠更斯原理，利用麦克斯韦方程组求解光通过小孔后的电磁波角分布，即可得到衍射图样.但严格的衍射电磁波求解需采用矢量场理论，计算较为复杂，而当衍射角度不大时，利用标量衍射理论即能较好的解决衍射问题，其数学表示形式为基尔霍夫公式.当衍射屏为小孔时，基尔霍夫公式可近似表示为［3］

其中，ψ0为原点处的场，k1、k2为入射波矢和衍射波矢，θ1、θ2为入射方向和衍射方向与小孔面法线方向的夹角，x和x'分别为空间中的场点和小孔面上的一点，S0为小孔孔面，ψ(x )2代表x处的衍射光强度.当入射光垂直照射到小孔时，k1·x'=0，cosθ1=1，则(1)又可进一步化简为

对于不同的衍射屏，只需要将(2)式中的积分计算出来，即可得到远处x处的场，其模平方为衍射光强度.当其与衍射角度为零时的光强做对比时，可得到相对光强.

当小孔形状为半径为a的圆孔时，由(2)式可得衍射光强为

其中，α为衍射波矢沿小孔面法线方向(z轴的方向)，I0表示当衍射角度为零时在z轴的衍射光强.

当小孔形状为边长a和b的矩形时，由(2)式可得衍射光强为

2 结果与分析

2.1 圆孔衍射

图2(a)给出了当圆孔半径为10微米，入射波长为500nm时的夫琅禾费衍射光强分布.由图可见，衍射光斑的能量大多集中于中心光斑(艾里斑)，中心处光强最大为1.在插图中可见，前三个次极明纹的峰值分别为0.0175，0.0042和0.0016，位置分别在5.14，8.42和11.6，而衍射光强值为零时的位置分别在3.83，7.02和10.17.说明随着衍射角度的增加，相比于中心明纹的峰值，次级明纹的强度迅速减小，第一个次级明纹的峰值已减小到1/60，并且其宽度也减小，而其它次级明纹峰值则更小，强度更弱，经过计算表明，艾里斑的能量占据了衍射光斑能量的大部分，达到84%［1］.还可以看到，第一个与第二个次级明纹的宽度和峰位几乎无差别，分别约为3.15和3.2，但次级明纹光强峰值所在的位置并不恰好在两个暗纹的正中间.另外，还需要指出的是，衍射光强为零的这些位置实际上是一阶贝塞尔函数为零时的数学解，因而衍射光斑宽度与波长成正比，即波长越大衍射光斑尺寸越大，但衍射宽度与圆孔尺寸成反比，即圆孔尺寸越大衍射光斑尺寸越小.图2(b)给出了衍射图样随波长变化的关系.

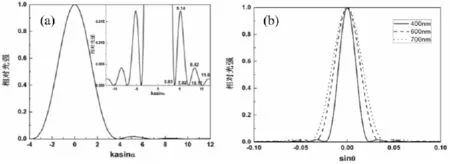
图2 夫琅禾费圆孔衍射(a)光强分布，(b)随波长变化关系

2.2 矩孔衍射

图3(a)为夫琅禾费矩孔衍射光强分布图.由图可见，矩孔衍射光斑的能量也大多集中于中心明纹处.由插图中可见，前三个次极明纹的峰值分别为0.0472，0.0165和0.0083，位置分别在4.49，7.73和10.9，而衍射光强值为零时的位置分别在3.14，6.28和9.42.说明随着衍射角度的增加，次级明纹的强度迅速减小，第一个次级明纹的峰值已减小到1/25，并且其宽度恰好为中心明纹宽度的一半，而其它次级明纹峰值更小强度更弱.还可以看到，矩孔次级明纹光强峰值所在的位置并不恰好在两个暗纹的正中间，稍微偏向于中心明纹的位置.但通过计算得知，随着衍射角度的增大，次级明纹的位置也越来越倾向于处在两个暗纹的正中间.矩孔衍射光斑宽度与波长也是成正比，即波长越大光斑尺寸越大，但衍射宽度与矩孔尺寸成反比，即矩孔尺寸越大衍射光斑尺寸越小.图3(b)给出了波长为500nm的光波垂直照射在长宽分别为20微米和40微米的矩孔表面所形成的衍射图样.由图可见，矩孔边长越大，则平行于其方向的衍射光斑尺寸约小，在同等视角内的光斑也越多，矩孔边长越小，则衍射光斑越分离;同时，在非平行于边长的位置，也出现了衍射光斑，但光斑强度均较弱.