不畏浮云遮望眼 深思熟虑子自知
——2012年浙江省数学高考解题追踪调查研究
2012-11-20温岭中学浙江温岭317500
● (温岭中学 浙江温岭 317500)
不畏浮云遮望眼深思熟虑子自知——2012年浙江省数学高考解题追踪调查研究
●孙海琴(温岭中学 浙江温岭 317500)
近几年的浙江省数学高考试题既重视基础知识与基本技能的考查,又力避学生熟悉的“解题套路”,深化了学科素养与思维的考查.现以2012年浙江省数学高考理科第17题为例,加以剖析和说明.
题目设a∈R,若x>0时均有[(a-1)x-1](x2-ax-1)≥0成立,则a=________.
笔者随机抽样调查了本校高三部分学生(40人)的解题情况.这是学生熟悉的“恒成立”命题,但成功解题的人却不多.其中22人选用“构造函数”方法解题失败,11人选用“变量分离”方法解题失败,11人转化为不等式解集关系仅有2人成功解题,转化为图像位置关系解题的有8人成功,利用特殊值解题的有5人成功.个别学生甚至尝试2~3种方法都解题失败,收集学生解答过程发现:面对困难,若能勇敢尝试,大胆突破,其实“条条大路通罗马”.
思路1构造函数
学生解答:因为[(a-1)x-1](x2-ax-1)≥0,所以
(a-1)x3-(a2-a+1)x2+x+1≥0.
设f(x)=(a-1)x3-(a2-a+1)x2+x+1,则
f′(x)=3(a-1)x2-2(a2-a+1)x+1.
出现困难:不等式
f′(x)=3(a-1)x2-2(a2-a+1)x+1≥0
的解集无法求.
突破困难:正确理解解不等式f′(x)≥0的意义,道是“不解”胜“详解”.
解法1当a=1时,显然不合题意.记
Δ=4(a2-a+1)2-12(a-1),

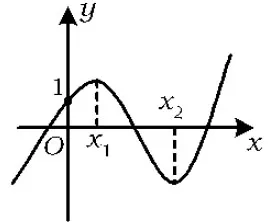
图1
图2
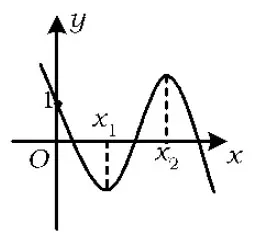
图3

图4

图5
再次突破:代数技巧“设而不求”能巧妙地避实就虚,实现“化繁为简”的目的.
解法2以数解形
若a-1≤0,则当x→+∞时,f(x)→-∞,因此a-1>0.因为x2-ax-1=0有2个相异实根,所以f(x)=0至少有2个实根.
(1)当Δ≤0时,f(x)在R上单调递增,f(x)只有1个根,故舍去.
(2)当Δ>0时,设f′(x)=0的2个根为x1,x2,且x1

表1 f (x)与f ′(x)的取值情况
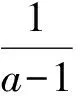
思路2解不等式组
学生解答:因为[(a-1)x-1](x2-ax-1)≥0等价于
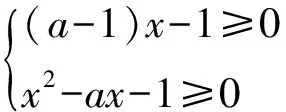
当a-1>0时,

首次突破:巧用符号在分类讨论中可达到“事半功倍”之效.
解法3记方程x2-ax-1=0的2个根为x1,x2,且x1
当a-1≤0时,显然不合题意.
当a-1>0时,


由题意可得
从而

即
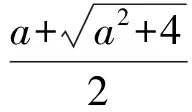
故
(二)教师应引导学生观察家庭生活。家庭同样是孩子的学校,同时也是孩子最放松、最熟悉的地带。家庭教育与学校教育关系密切。教师应当鼓励家长积极主动参与学生的校外学习,同时鼓励学生在家中观察家庭成员、记录家庭事件,从而积累丰富的写作素材。比如,教师引导学生记录家事,引导学生记录下家里发生的难忘的事情、开心的事情、难过的事情等等。这样一来,家庭琐事、家庭成员的活动等等也将成为孩子写作素材的一大来源,记录家庭事件可以充分激发学生的积极性,激励孩子写出真实而不套路的文字。

再次突破:高次不等式转化为不等式组有“化简为繁”之嫌,零点分区间讨论是解决高次不等式的有效手段.
解法4当a-1>0时,原不等式等价于

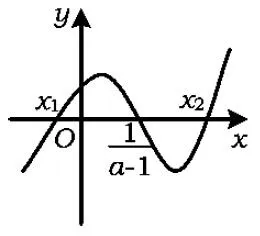
图6

图7

图8
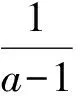
思路3参变量分离转化成求最值问题
学生解答:因为[(a-1)x-1](x2-ax-1)≥0等价于
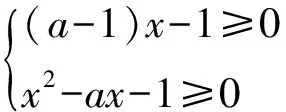
所以

从而

故
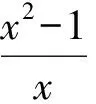
首次突破:只有正确理解“或”才能避免此类“失误”.
解法5结合y=x2-ax-1的图像(如图9所示)可以发现:
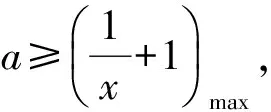

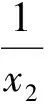

图9
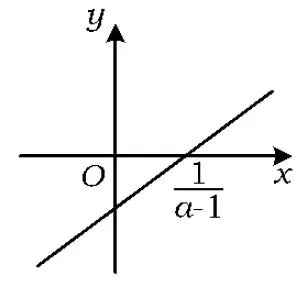
图10
解法6由y=(a-1)x-1的图像(如图10所示)可以发现(其中a-1≤0不合题意):
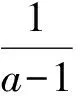
再次突破:优化解法5和解法6.
思路4考察2个函数图像的位置关系
解法7学生解答
在同一坐标系作出y=x2-ax-1及y=(a-1)x-1的图像,显然2个函数都过定点(0,-1).记方程x2-ax-1=0的2个根为x1,x2,且x1

图11

图12

图13

图14
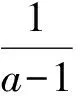
解法8以数解形
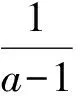
三次突破:变量分离的实质是变更主元.
思路5变更主元
解法9以a为主元,由原不等式可得
[ax-(x+1)][ax-(x2-1)]≤0,
因此

又a是一个确定的值,由两边夹原理可得

从而
x=2,
故

解法10将ax看成主元,由原不等式可得
[ax-(x+1)][ax-(x2-1)]≤0,

图15

思路6特殊值法
解法11学生解答
当x=1时,0≤a≤2;

本题作为填空题的最后一题,具有一定的难度和区分度,思维的切入点较多,思维空间较大,为不同水平的学生提供了不同的发挥空间.本题由学生熟悉的习题改编而成,考生虽有似曾相识的感觉,但往往被“浮云遮望眼”,此时需要信心,需要通过观察、联想、分析、转化来达到“深思熟虑”,突破困难,进而达到“子自知”的境界.此题对加强数学思维论、方法论教学,避免陷入盲目、机械的解题训练起到了很好的导向作用.
