看似平凡 意蕴不凡——2012年一道高考翻折题引发的思考与启示

● (衢州市第二中学 浙江衢州 324000)

看似平凡意蕴不凡——2012年一道高考翻折题引发的思考与启示

●傅建红(衢州市第二中学 浙江衢州 324000)

( )

A．存在某个位置，使得直线AC与直线BD垂直

B．存在某个位置，使得直线AB与直线CD垂直

C．存在某个位置，使得直线AD与直线BC垂直

D．对任意位置，3对直线“AC与BD”、“AB与CD”、“AD与BC”均不垂直

这是2012年浙江省数学高考理科试题中的一道选择题.初看，其背景朴实、平淡，是立体几何中常见的翻折问题.但细品之下你会发觉，此题虽题目简洁，但构思新颖，可谓朴素中透着灵气，脱俗中不失新颖，令人赏心悦目却又回味悠长.题目借立体几何中常规的矩形翻折问题为载体，考查“动态”变化过程中的线线位置关系，入口“亲切平和、似曾相识”，使不同层次的学生都会有一些思路，但要完全解决则需要一定的空间想象能力，尤其是应具有思维的灵活性.本题作为选择题最后一题，看似平淡却意蕴不凡，是试卷的一大亮点.

1 预备知识

翻折问题是立体几何中的重要问题.由于翻折使立体几何由“静态”转化为“动态”，因此，它能充分考查学生的抽象思维能力.由于翻折使得图形中部分几何元素的位置关系、数量关系发生了变化，因此，如何捕捉这种变化过程中的不变性及相互关系是解决这类问题的关键.本文首先介绍翻折问题中的有关性质、公式，以便为下面的解答作一些铺垫.

性质1(平面翻折性质Ⅰ)如图1，将△ABC沿直线AB折起至△ABC1，则AB⊥CC1.

证明如图1，过点C作CH⊥AB，垂足为H，联结C1H，则C1H⊥AB(因为C1H是CH经平面翻折后的线段)，于是AB⊥平面C1HC，从而AB⊥CC1.

图1

图2

性质2(平面翻折性质Ⅱ)如图2,将△ABC沿直线AB折起至△ABC1，设点C1在△ABC所在平面内的射影为O，则OC⊥AB.

证明如图2，因为C1O⊥底面ABC，所以AB⊥C1O.又由性质1知AB⊥CC1，于是AB⊥平面C1OC，从而AB⊥OC，即OC⊥AB.

说明翻折问题的实质是平面绕轴的旋转问题.如图1，在平面ABC绕轴AB旋转过程中，由于CH⊥AB，因此动点C在空间运动的轨迹就是以点H为圆心、以CH为半径的圆，显然直线AB过圆心且垂直于这个圆，而C1C是该圆的一条弦，故AB⊥CC1.同理，由于C1O⊥底面ABC，可知C1O与OC也都在垂直于AB的这个圆内，故AB⊥OC.

图3

性质3(三面角公式)如图3，已知∠AOB=α,∠COB=β,∠AOC=γ,点B满足AB⊥OB,CB⊥OB.设二面角A-OB-C的大小为θ，则

cosγ=cosαcosβ+sinαsinβcosθ.

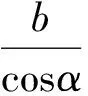
AC2=b2tan2α+b2tan2β-2abtanαtanβcosθ,

从而在△AOC中，由余弦定理

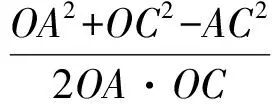
将上述OA，OC，AC代入并整理即可得证.

说明此性质在立体几何中称为三面角公式(也称三余弦公式)，它所刻画的是由3条不共面的射线(此处即为OA，OB，OC)所构成的3个平面(此处即为面AOB，BOC，AOC)中，已知某2个面内2条射线所成的角以及这2个面的二面角，即可求出另一个面内2条射线所成角.如上，已知α,β及θ即可求得γ.而且这种表示是任意的，如图3，假设二面角B-OC-A的大小为φ，二面角C-OA-B的大小为δ，则同样也有

cosα=cosγcosβ+sinγsinβcosφ,

cosβ=cosαcosγ+sinαsinγcosδ.

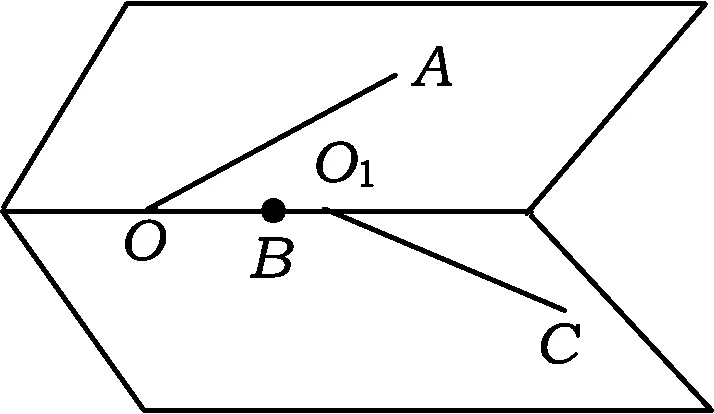
图4

特别地，当某二面角为90°时，比如θ=90°时，cosγ=cosαcosβ(三余弦).另外，此公式应用的前提是3条射线共点但不共面，而且它们之间所成的角都是指射线与射线的夹角(这一点非常重要).若3条射线不共点(或不完全共点)，比如图4中的OA,OB,O1C，则必须将它们平移到同一点，并重新考虑3条射线两两所成的角，方可使用此公式.

2 解法思考

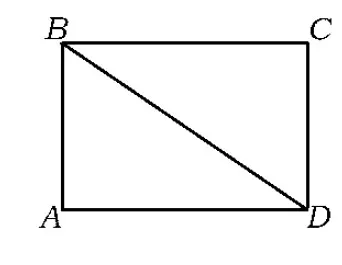
图5

图6

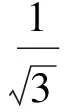
因此存在θ=60°使得cosγ=0，即γ=90°，故选项B正确(即选项D错误).最后考虑选项C，假设射线DA与BC所成角为φ，同样经过平移，由性质3可得

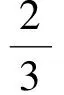
显然不论θ取何值，cosφ恒不为0，即φ恒不等于90°，即选项C错误.故本题答案是B.

点评本题的难点在于“动”，而翻折是引起“动”的根源，它使得问题时刻处于动态变化过程中，让人感觉空灵无助、捉摸不定，不知从何处寻找问题突破口.但辩证法告诉我们，事物的变化是有规律的，本文上述的性质、公式正是把握了这种变化过程中的不变性和相互联系，揭示了翻折问题的客观规律，不仅对本题，而且在其他翻折问题中同样具有较强的现实意义.本题中，选项A的判断使用了性质1和性质2，通过反证法使问题获得解决；而选项B和选项C的判断均使用了性质3(性质3是解决立体几何中线线角、二面角问题的“利器”)，但性质3运用的前提条件是3条射线共点，而本题环境并不具备此条件，因此首先需要经过平移来实现三线共点(务必考虑平移前后角度的变化)，然后再使用性质3即可使问题获解.

思考2(空间向量法)我们知道，空间向量是解决立体几何问题的“利器”，用它来判断线线垂直，只需考察其数量积是否为0.但在此翻折问题中能否用得上呢？

图7

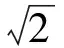
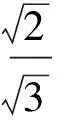
由AM⊥底面CBD，得A0H⊥BD，从而

∠BA0H=∠A0DB.

过点M作MN⊥AB，垂足为N，则

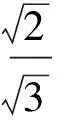
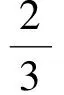
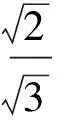
从而

故

这说明无论θ如何变化，AC与BD以及AD与BC均不可能垂直；而当θ=60°时，AB⊥CD.故选B.

点评上述解法表明在翻折问题中仍可使用空间向量法.但关键在于能否求出动点坐标(定点坐标相对简单)，动点坐标一旦突破，则整个问题就会豁然而解，比如本题中点A的坐标.如前所述，翻折是引起图形中一切“动”的根源，但这种“动”的最本质数字特征是什么呢？其实就是翻折前后2个平面所成的二面角，而二面角的大小用其平面角来刻画，因此，一旦我们作出二面角的平面角，那么动点坐标也就迎刃而解了.而在翻折问题中，要作出二面角的平面角只要运用前面的性质2即可轻松解决.

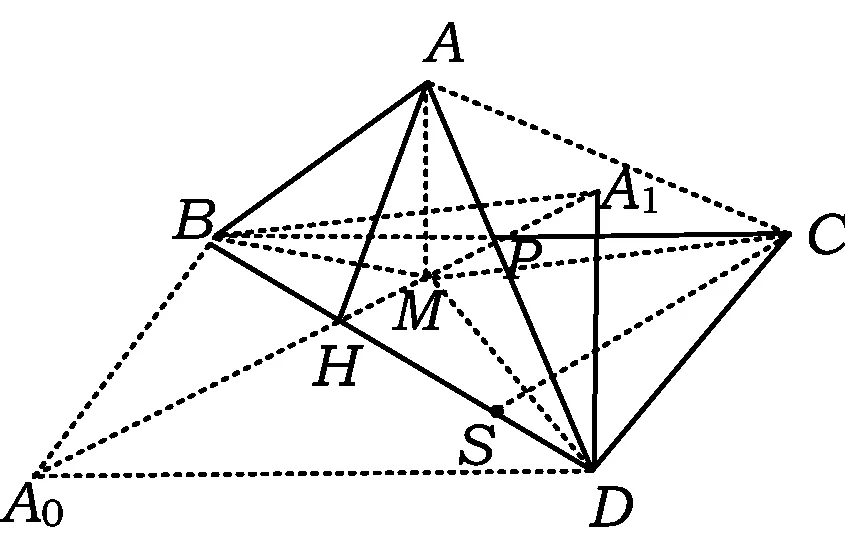
图8

思考3(三垂线定理法)回眸上述2种思路，均站在理性的高度上，从2个不同角度深入剖析问题的实质，并逐渐揭开了试题的“神秘面纱”.方法不可谓不巧妙，论证也不可谓不精到，对于数学探究而言确应如此.但如果我们站在考生的立场上试想一下，作为一个选择题，如此不计“成本”的“大动干戈”值得吗？笔者认为，多数考生不会如此深入，这也有违命题者的初衷.那么，本题究竟要考查学生什么呢？其实，许多看似复杂问题的背后往往隐藏着朴素的思想，本题实际考查的只是立体几何中一个基本定理——三垂线定理.如图8，过点C作CS⊥BD，则CS∥A0H.当θ=180°时，点A在A0处；当θ=0°时，点A在A1处，因此，当θ从0°到180°的渐变过程中，动点A在底面上的射影M的运动轨迹即为线段A1A0.设A1A0与BC的交点为P,先看选项A，由三垂线定理，如果AC⊥BD，则MC⊥BD，又CS⊥BD，从而点M,S重合，这是不可能的(因为CS∥A1A0)；再看选项B，欲使AB⊥CD，只要MB⊥CD，而这一情形只要当点M运动到点P时即可实现(因为BP⊥CD)；最后看选项C，欲使AD⊥BC，只要MD⊥BC，而CD⊥BC，故点M重合于点C，而这显然也是不可能的(因为点M在有限的线段A1A0上运动).综上可知，只有选项B正确.

点评至此,终于完全掀起了题目的“盖头”，破译了其中蕴含的“神秘玄机”.原来本题真正考查的是翻折问题中如何使用三垂线定理来证明线线垂直，但题目立意之深，内涵之广，背景之妙，使人感觉不露痕迹，不易识破.而且其“于平淡中见神奇，于常规中透奇意”的命题手法耐人寻味，真可谓是匠心独具.为什么看似熟悉却常常无从下手？为什么不能在第一时间运用三垂线定理？究其原因是我们未能识破问题背后蕴含的玄机，具体来说就是对翻折问题的本质(性质1和性质2)把握不够，即使想到了三垂线定理，也似“雾里看花”难以真切.而如果我们了解翻折问题的本质，即知道动点A在底面上的射影M的轨迹是一条垂直于“折痕”(二面角的棱)BD的线段A0A1，这时再利用三垂线定理那就显而易见了.

3 教学启示

3.1 高三复习要善于“借题发挥”

本题源于一类常见的立体几何翻折问题，命题者将设问进行了巧妙地移植.经过包装的试题给人“似曾相识”的感觉，但又与平时的题目不一样，使依靠“题海战术”的考生不占优势，因此，它能很好地考查学生的真实水平.为什么考生对此“似曾相识”却往往又无从下手？根本原因是：虽然平时遇到过类似问题，但都未能从本质上搞清问题的来龙去脉，即未能真正领会其精髓，一旦重新遇到，虽表面“似曾相识”而实际却无可奈何，只能望题兴叹.那么针对这一现象，作为主导者的教师，应如何应对？《普通高中数学新课程标准》(实验)指出：要强调对数学本质的认识，否则会将生动活泼的数学思维淹没在形式化的海洋中.因此，笔者认为，教师在平时的教学过程中(尤其是在高三复习阶段)，要引领学生借练习、试卷中出现的类似“好题”(有探究价值的习题)为载体，进行“借题发挥”多方演绎，充分挖掘问题本质.具体地说就是与学生一起对“好题”进行深入地剖析、引申、类比，让学生“亲历”知识发生、发展的全部过程.在此过程中，教师要舍得花时间，切忌浅尝辄止、就题论题.这种“借题发挥”看似浪费了时间，实际触及问题的核心和思维的灵魂，使学生能真正领会问题的实质，因此常可收到事半功倍的效果.

3.2 立体几何教学应注重“双管齐下”

立体几何是新课程教材中变化最大的一块内容，其考查内容兼顾传统几何法和空间向量法.但随着空间向量的引入，它以其在求空间角、空间距离方面的巨大优势而越来越受到师生的关注和喜爱，成为了解决立体几何问题的首选方法，大有后来居上取代传统几何法地位之势，这使得有些传统的几何方法被逐渐地淡化，有些甚至被打入“冷宫”不再提及(比如三面角公式).针对这一现象，笔者认为此举颇不可取，传统几何在中学教材中由来已久，它的存在必定有其合理性和价值，诚然，向量法因关注计算淡化技巧，常可降低问题的思维难度，使学生容易上手.但是在有些问题中，尤其是在证明题中，使用传统几何法的定理来证明常显得十分简捷明快，而使用向量法则显得异常繁琐、笨重，况且空间向量法的前提是建系并标出点的坐标，而在某些“恶劣”环境下，建系标点将是十分困难的(比如本题的翻折环境)，这时利用向量法不仅没有优势，而且增加了问题的难度，使简单的问题复杂化.因此，笔者认为，几何法和向量法在立体几何教学中应两者兼顾，双管齐下，不能厚此薄彼，甚至顾此失彼.

3.3 临场应试仍需要策略指导

笔者对部分学生进行了调查，发现有部分成绩好的学生没有答对本题，而一些平时成绩一般的学生反而答对(如：高考成绩为131的学生甲答错问题，而高考成绩为92分的学生乙答对问题).笔者经了解后得知，生甲一开始就从正面突破，但没算出来，之后就放着先做下面的题目，到后来就没时间了，只能胡乱猜一个，结果猜错了；而生乙根本没有去计算(其实不会)，只是用一张矩形的草稿纸折了一下，通过直观操作大致猜了一个最有可能的答案，结果刚好猜对了.这一现象说明：立体几何中动手操作、直观感受有时也是一种有效方法.生甲采取的是“小题大做”，而生乙采取的是“小题小做”，解答的不同策略导致了不同的结果.回想新课程中立体几何的许多性质、结论并不要求学生严格证明，而只需直观感受、操作确认，因此笔者认为命题者是鼓励学生运用猜想的方法解决该题的，生乙的解法正与这种思想不谋而合.由此可见，高考应试的策略也是极为重要的，教师应根据不同程度的学生给予不同的指导，做到有的放矢、对症下药.

[1] 沈良.例谈空间几何中翻折问题的解决策略[J].数学通报,2011(7)：33-36.

[2] 庄丰.貌似平淡 内涵丰富[J].中学数学,2011(10)：13-15.