一道2012年大纲全国卷高考试题的推广
2012-11-20华南师范大学数学科学学院广东广州510631
● (华南师范大学数学科学学院 广东广州 510631)
一道2012年大纲全国卷高考试题的推广
●李海梅(华南师范大学数学科学学院 广东广州 510631)
2012年数学高考大纲全国卷理科第12题很有趣,与平时的打桌球游戏非常类似,题目如下:

( )
A.16 B.14 C.12 D.10
本题主要考查反射原理与三角形相似原理的应用,同时考查综合运用数学知识进行推理论证的能力.
参考答案:结合已知点E,F的位置,进行作图,推理可知,在反射的过程中,直线是平行的,那么利用平行关系作图,可以得到回到点E时,需要碰撞14次.
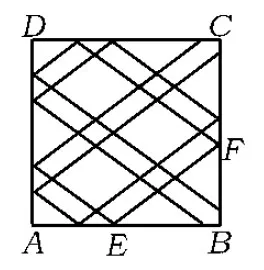
图1
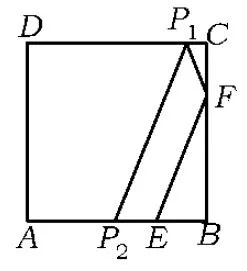
图2
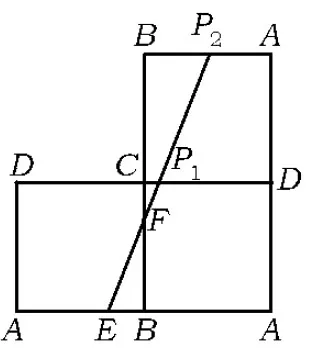
图3
用几何画板作图,如图1所示,从图1中可以看出,仅用尺规作图过程相当繁琐,一招不慎,满图皆乱,而且无法推广到一般的情形.
本文借助于物理中的光学知识,把点P的运动轨迹由折线化为直线,给出下文的解法并推广到一般的情形.根据入射角与反射角相等法则,光线走向(直线)按反射面(直线)翻折后与反射前光线走向(直线)应该是一条直线[1].图2所示为光线在正方形ABCD内的行进,图3所示为正方形ABCD的边按对称翻折后所作成的平面图形,可以把光线看成是直线行进的.因为点P每与正方形的边碰撞一次就会引起一次翻折,故由翻折的次数,可推出碰撞的次数.

解点P的运动可以看成光线在正方形ABCD内的行进.作出正方形的边按对称翻折后所作成的平面图形,如图4所示,可以把点P的运动看成是沿射线EF运动的.现证当点P运动到点G处时,点P第一次碰到点E,由图4可知,只需证AE=A′G即可.
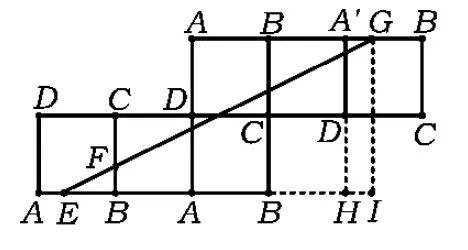
图4
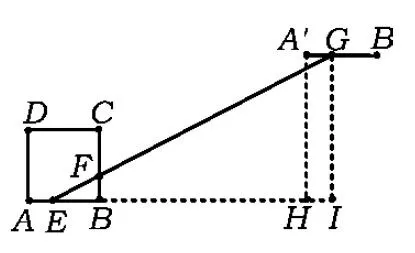
图5
对于一般的情形,经过笔者研究,可得出以下结论:
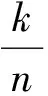
参考以上解法,可作如下证明.

因为(n,k)=1,所以(n-k,k)=1.又因为EI,GI皆为偶数,所以t必为偶数,令t=2i(i∈N*).当i=1时,即为点P第一次碰到点E,此时EI=2(n-k),GI=2k,可得正方形ABCD向右翻折了2(n-k)次,向上翻折了2k-1次,故当点P第一次碰到点E时,点P与正方形的边碰撞了2n次.由对称性可知,分别与AB,CD碰撞了k次,分别与BC,AD碰撞了n-k次.
本文把原题的条件推广到了一般的情况,那么当AE与BF不相等的情况呢?当点P以任意的角度从点A出发,小球是否会回到点A?这些有趣的情况就留给读者去探究吧.
[1] 苟玉德.一道数学高考题的物理解法及启示[J].数学教学,2003(11):48-49.
