抓住变式源头 积累转化经验 优化复习设计

● (萧山中学 浙江萧山 311201)

抓住变式源头积累转化经验优化复习设计

●瞿少华(萧山中学 浙江萧山 311201)

师生在高三复习中常常会遇到两大困惑.困惑之一：对教师而言，有那么多的题型、方法、思想要教，要让学生真正掌握，到时用得上，用得正确，深感头绪多，复习时间不够用.困惑之二：对学生而言，做了那么多的题目，把常规题型、常规方法都熟记在心，但一碰到需要观察、分析、转化的问题，还是一筹莫展，与掌握的知识方法挂不上钩.当然，造成上述困惑的原因是多方面的，笔者与同事从改进复习课的教学设计入手，通过帮助学生“抓住变式源头”和“积累转化经验”两大抓手，对突破高三复习课困惑进行了有益的探索、实践和思考，有一些收获和感悟，以求教于同行.

1 从有利于学生抓住变式源头的角度进行课堂教学设计

数学中的基本原理、基本方法、基本思想一定是简单的，但简单中往往蕴含深刻、强大，在不同的情景下，其表现形式是变化多端的.考查不同情景下学生的运用能力，正是高考的考点之一.老一辈数学家曾说过，读数学要“从薄到厚，再从厚到薄”.前半句话师生有较多办法，后半句“从厚到薄”则常常缺少办法.笔者认为，学会抓住变式源头，不失为一种有用的办法，或者说抓手.所谓变式源头，主要是指许多题型、技巧、方法从联系的观点看，常常可以追溯到某些源头——基本数学模型或者基本思想方法.只不过我们限于自身的水平，常常没有看到，如果教师能让学生从源头上真正理解和掌握现象的客观规律，掌握解决问题的思想方法，则改头换面出现的题型、技巧通常可以解决，即使学生形成知识、方法、思想的有用认知网络，所谓做一题及一类，事半功倍.

案例1解斜三角形中，边、角诸元素的范围探究

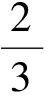
设计意图给出已知一角和一对边的典型情景，作为变式源头，让学生通过几何直观、函数思想、不等式和向量问题，综合探究三角形边角诸元素的范围，剖析典型问题的特征，体会典型思想方法的应用.

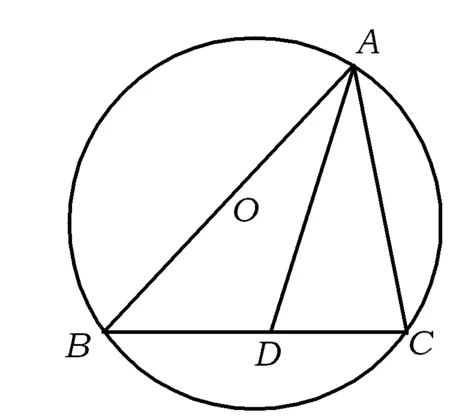
图1

(2)让学生体会用函数思想进行研究.函数是揭示变量之间关系最常用的工具，边与角、角与角相应变化关系，使我们容易得到所求元素是用边或角表示的一元函数.由正余弦定理得

从而

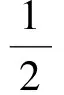
得

从而

(3)对于处理范围问题，不等式也是一个有力的工具，特别是均值不等式，要熟练运用.由余弦定理得

b2+c2-bc=3,(b+c)2=3+3bc2，

由均值不等式可得

又因为

所以

同理可得

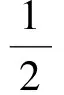
从而

于是

因此

又因为

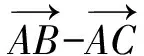
而

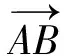
得

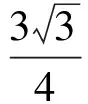
同理可得

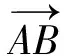
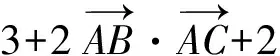
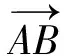
于是

即

学生在这样的典型问题、典型思想方法中若能真正理解和掌握，则许多解三角形问题都能看成源头的一个变形，是数学思想方法的一个很自然的运用，使学生能马上抓住解决问题的关键.

2 从有利于学生获取转化经验的角度进行教学设计

理解和掌握基础知识、基本方法、基本思想，能从变式问题的源头真正搞懂，对学好数学无疑是十分重要的，但仅停留在这一步，还是远远不够的.把新问题、新面孔转化为基本知识、基本思想方法和变式的源头，学生常常缺少经验，这是我们高三复习中急需解决的另一困惑.认知心理学认为：“新手”与“老手”在解决问题上的主要差异，不在于知识的多少，而在于经验的差异，而经验需要在平时学习中有意识地积累.因此在课堂教学设计中，要特别注重帮助学生获取非常规题转化为常规题的经验，或者说，变式问题转化为变式源头的经验.

案例2解析几何和不等式问题中一些转化思想和经验的归纳获取

设计背景解析几何是用代数方法研究几何问题，体现了方程、函数、图形之间很强的综合性和转化关系.不等式更是上述知识方法的一个集合.这类教学内容是让学生获取转化经验的较好素材.

设计意图通过以下例2～例5的教学设计，使学生获取“把未知函数转化为已知函数”、“把数、式问题转化为已知图形问题”、“把结论未知问题转化为结论已知问题”、“把非规范问题转化为规范问题”等转化经验.

例2若a,b,c成等差数列，则原点O到直线ax+by+c距离的最大值为______.

(1)通过消元法(倒数)，把未知函数值域转化为已知函数值域，是学生从中获取的经验之一.

设距离为d，则

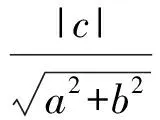
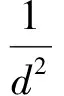
因此

(2)通过方程几何意义，把数、式问题转化为已知图形问题，是获取的经验之二.

或由2ax+2by+2c=0得

a(2x+y)+c(y+2)=0，

从而得直线恒过点(1,-2).

(3)用合情推理——特殊到一般转化，把结论未知问题转化为结论已知问题，也是获取的基本经验.

举出特例得出直线恒过点(1,-2)，易得一般结论.

类似的思想方法和经验，在2012年江苏省数学高考第14题难点突破中很有用.

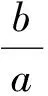
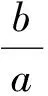
e≤y≤7.

5-3x≤y≤4-x，y≥ex，

创设条件把非规范问题转化为规范问题也是转化的基本经验之一.

三维柯西不等式的一个变式通常是许多分式轮换不等式的一个源头.

由

得

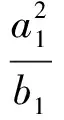
它特别和谐“规范”，而一般分式不等式常不够规范.如何创设条件让它规范是学生应获取的经验.

例4设x，y，z是正实数，且x+y+z=1.

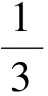
(2012年杭州市数学高考一模试题)

证明(1)可以直接应用柯西不等式的规范变式

(2)让分子“规范”：x4=(x2)2易转化为规范变式

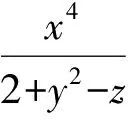
当x=y=z时等号成立.

例5如果x，y，z为正数，求证：

3(xy+yz+zx)]；

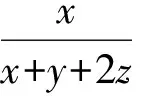
(2012年杭州市数学高考二模试题)

证明(1)左边展开、比较即可(略).

(2)让分子“规范”：分子分母分别乘以x,y,z,得

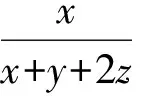
当x=y=z时等号成立.