结合扩展LoB滤波的距离保持水平集方法
2012-11-18付茂臣任泽民
秦 进,付茂臣,任泽民
(1.遵义师范学院数学系,贵州 遵义563002;2.重庆大学数学与统计学院,重庆 400030)
图像分割是低层图像处理的基本问题之一,目的是把目标从图像背景中分离出来。目前,已提出很多图像分割的方法,基于水平集的几何活动轮廓模型能较好地解决图像中拓扑结构改变的分割问题而被广泛应用[1-3]。基本思想[3-5]是:把演化曲线(活动轮廓)隐含地表示为一个高一维函数(水平集函数)的零水平集,水平集函数在一个偏微分方程(组)的控制下进行演化,直到零水平集演化到图像的目标边缘为止。
几何活动轮廓模型通常可分为边缘模型和区域模型两大类。它们在图像分割应用中各有千秋,分割效果的优劣取决于图像所具有的特征。本文讨论边缘模型。
边缘模型[1-5]主要依赖边缘停止函数使演化曲线停止在目标边界上,距离保持水平集方法[6]就属于这种模型。该方法引入内能量泛函来纠正水平集函数与符号距离函数的偏差,因此无需在演化过程中再周期性初始化水平集函数。同时,该方法可采用简单的有限差分法和较大的时间步长求解相应的偏微分方程,大大提高了水平集演化的速度。然而,这种方法仍然存在明显的缺点:(1)模型以图像的一阶微分(梯度模)平滑度量为基础,不能适应仿射变换,可能会直接影响模型的实际应用;(2)初始嵌入函数与被分割图像无关,当初始轮廓与目标边缘较远时,其位置将直接影响分割时间;(3)能量泛函的权系数不能根据图像信息自适应调整符号和大小,因此零水平

考察区域内数据之和最小,则白色椭圆必须“演变”成枫叶的形状,使考察区域的边缘“停止”在区域交界的二阶微分过“零点”处。这样可利用图像灰度值二阶微分在“零点”附近,正负符号相反的效应,构造新的能量控制泛函。
顺便指出,由于 B(x,y)=B(x)×B(y)的乘积可分的性质,故可利用 B(x)和 B(y)两个一维滤波器,分别在水平和垂直方向独立卷积,来降低算法时间复杂度;另一方面,从式(6)也得到,二维算子 B(x,y)具有保持仿射变换的性质。
2.2 结合扩展LoB滤波的距离保持水平集演化
从2.1可知,改进LoB边缘检测算子可以区分图像边缘区域和非边缘区域,将图像二阶微分度量Le(g)作为嵌入函数的权值,求其加权面积,将得到一个代替式(1)等号右侧的第三项新的能量泛函
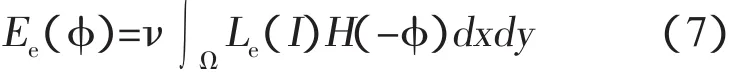
其中,φ是嵌入函数。
利用梯度下降法极小化被式(7)替换后的式(1)这个泛函,得到新的控制水平集演化的偏微分方程

3 数值实现
在数值实现(8)时,Dirac函数 δ(x)采用了式(5)定义的正则化Dirac函数。本文实验选取ε=1.5。
假设Ω0是图像区域Ω的一子集,∂Ω0是Ω0的所有边界点的集合,初始水平集函数φ0可以如下定义

式中,ρ>0为常数,一般取值为ρ≥2ε,由于二阶微分度量Le(g)的边缘特征比较明显,故初始嵌入函数的选择可以很平坦,如ρ=1。
对于式(8)的第一项,拉普拉斯算子△φ的离散,可采用简单的4邻点差分格式,即

而散度部分用中心差分法近似代替φx,φy为

进一步单位化
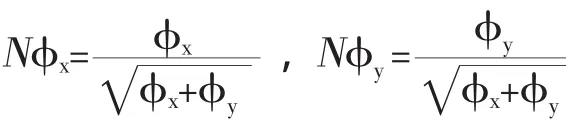
故

对于新的项新增加的速度保持项目是常数,直接使用图像的空间离散化,即
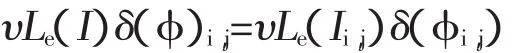
式(8)涉及第二项可采用具有二阶精度的中心差分格式实现。采用“半点离散化”方案。
由于

上式中的每一项,可以用φ和g在整点的值近似表达。先离散化上式第一项有

所以
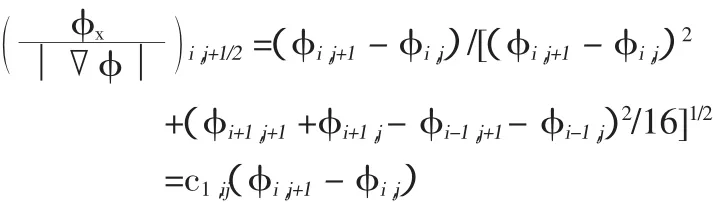
其他几项处理方式类似,得到
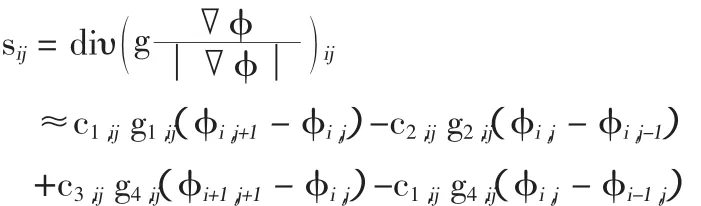
采用迎风方案,得到公式(8)的显式方案
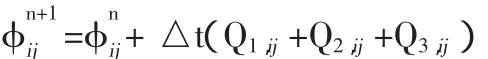
其中,
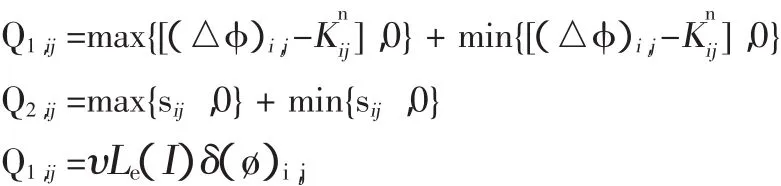
4 实验结果
本文方法对有尖角、狭窄边界的目标分割效果较好,可按照人们的需求得到分割目标的内外轮廓,同时较原模型演化速度提高了近10倍。
在所有实验中,对于两个模型共有的参数(λ、ν、μ等),取值与文献[9]一致。核函数参数σ与原文一致,按照n=σ2/pq的关系确定二项式滤波的参数。
实验平台是操作系统为Windows XP的PC(3.00GHz CPU/256MB内存),程序用MATLAB 7.1编写。
在图2中给出了本文方法和文献[10]的分割对比结果。大量试验证明:本文方法提高了近10倍的演化速度。而在细节捕获方面,本文方法分割的目标边缘精确度要高于文献[10]。
图2(1)给出了一幅带有尖角特征的枫叶(128×128)图像分割结果。本文方法,迭代20次(如图2(a))后就较好的分割出目标,特别是对枫叶的叶尖角细节捕获较好;而文献[10]方法迭代300次只可以粗略找到目标边界(如图 2(b))。
图2(2)是一幅典型的带有深陷特征、狭窄缝隙的(128×128)图像。经过25次迭代本文方法就达到稳定状态,精确捕获到目标的边缘(如图2(c));而文献[10]经过300次迭代却只是大致分割出目标的外边缘,而在具有较深凹陷的区域分割也不理想(如图2(d))。

图2 本文与文献分割结果与演化次数
有些条件下,人们可能对目标轮廓的需求不同。适当调节本文方法加权面积的系数,就得到目标内外边缘。图3是83×65细胞图像的分割结果,当ν=2.7 时,细胞的内外轮廓均被检测到(如图 3(a));当ν=0.9 时,得到的仅仅是细胞的外轮廓(如图 3(b)),而文献[10]方法无论系如何选取只能得到细胞图像的外轮廓(如图 3(c))。

图3 两种方法的细胞图像分割结果与演化次数
5 结论
本文提出的扩展LOB滤波的距离保持水平集方法很好地克服了原方法的上述缺点。实验表明,这种改进在快速、精确定位更丰富的目标边缘,分割目标内、外轮廓特征方面效果明显。
[1]V Caselles,F Catte,T Coll,et al.A geometric model for active contours in image processing[J].Numer Math,1993,66(1):1-31.
[2]Caselles V,Kimmel R,Sapiro G.Geodesic active contours[J].Int J Comput Vison,1997,22(1):61-79.
[3]Weickert J.Anisotropic Diffusion in Image Processing[M].ECMI Series,Teubner-Verlag,Stuttgart,Germany,1998.
[4]IEEE Computer Society Conference on Computer Vision and Pattern Recognition,2005.430-436.
[5]冯玉玲,何传江,李梦.不用高斯平滑的边缘活动轮廓模型[J].计算机工程与应用,2010,46(36):192-194.
[6]Li C,Xu C,Gui C,et al.Level set evolution without reinitialization:a new variational formulation:A new varictional formnlation[C].IEEE Computer society Conference on Computer Vision and puttern Recogni-tion 2005.430-446.
[7]许志祥,王积杰.二项分布-拉普拉斯和离散的高斯-拉普拉斯边缘检测算子的性能[J].电子学报,1992,(2):23-26.
[8]吴立德.概率论[M].北京:人民教育出版社.1979.
[9]Yang C,Zheng S,Ye J.Level set contour extraction method based on support value filter [J].Applied Mathematics and Computation,2008,(25):688-696.
[10]Li C,Xu C,et al.Fast distance preserving level set evolution for medical image segmentation [C],The 9th International Conference on Control,Automation,Robotics and Vision,Singapore,2006.126-138.
