映射观下的排列问题

2012-11-18陈明

遵义师范学院学报 2012年6期

陈明

（遵义师范学院数学系，贵州遵义563002）

排列问题是中学数学内容中的一个难点，主要表现在学生对其定义及表述难以理解，对解题思路及方法难以掌握。中学数学教材对排列问题的处理方式毫无异议，它主要是根据学生的认知特征来确定的，但作为教师自身仅限于此是远不够的，还应用现代数学的观点去揭示它，即弄清它的理论本质。为此，本文用集合、单射、计数的观点对排列进行了较深层次的阐释，不仅说明了现代数学与中学数学在这一部分内容的内在联系，而且有助于教师对该问题的认识。

文中所讨论的集合均为有限集。为方便，记#A表示集合 A 的元素个数，Nn=｛1，2，…，n｝表示从 1 开始的n个自然数的集合，I（Nm，A）表示映集Nm到集A所有单射组成的集合。关于集合的映射计数法，可作如下定义。

定义若#A=n，当且仅当存在着一个双射f∶A→Nn。

显然，若 #A=ø，当且仅当 #A=0。

在定理的证明中，本文用到了如下引理。

引理[1]若函数 f∶B→D，h∶C→A 均为双射，则有等价I（A，D）≈I（C，B）

众所周知，排列问题乃计数问题，而在集合论中，运用映射计数是较为典型的思想方法，为阐明排列问题与映射的关系，先看一个简单的例子。

例1有5本不同的书，准备分给3名同学，每人1本，共有多少种给法？

将三名同学编号为1，2，3，他们组成集合N3=｛1，2，3｝。同样，5 本不同的书组成集合 A=｛a1，a2，a3，a4，a5｝。对任意一种给法：如 a5给 1；a3给 2；a1给 3，唯一确定由N3到A的一个单射（如图1）。

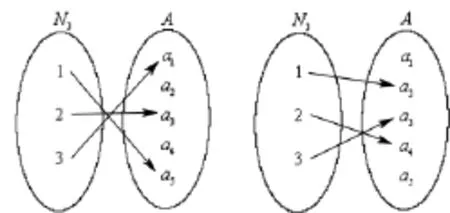
图1 N3到A的一个单射图2 N3到A的任一单射

反之，由N3到A的任一单射（如图2），同样也唯一地确定了一种给法：a2给 1；a4给 2；a3给 3。

由此可看出，“给法”与I（N3，A）之间具有一一对A）。将这一结论推广，得到定理1。

从而，计算#I（Nm，A）就转化为计算#I（Nm，Nn）了。

下面对m分m=0和1≤m≤n两种情况讨论如下：

（1）若 m=0，有

且对∀θ∈I（Nm，Nn），定义ν（θ）≜θ│Nm-1。

由于θ是一对一的，所以，ν（θ）也是一对一的。故∀θ∈I（Nm-1，Nn）。因此，ν的定义是有意义的。

现不妨设φ为I（Nm-1，Nn）中的任一元，且对应关系（如图 3），（其中 ai∈Nn）

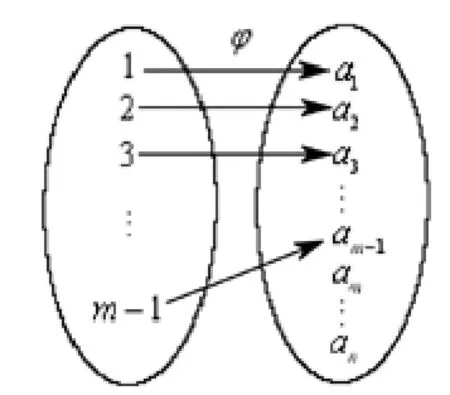
图3 φ的对应关系

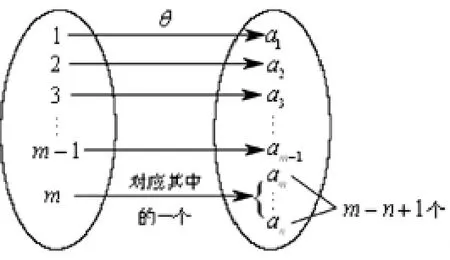
图4 θ的对应关系

显然，φ是图4中映射θ在Nm-1上的限制，故φ=θ│Nm-1，而 θ 又显然是属于 I（Nm，Nn）的，所以，ν是在上的。

另外，由图 4 显见，当 θ（m）对应｛am，am+1，…，an｝中n-m+1个的每一个时，得到I（Nm，Nn）中的n-m+1个单射。即是说I（Nm，Nn）中有n-m+1个单射在Nm-1上的限制都是φ，从而可推得φ具有如下的性质：

故当φ取遍I（Nm-1，Nn）时，I（Nm，Nn）就是诸集合ν-1｛φ｝的并。

显然，诸集合ν-1｛φ｝是互不相交的。

事实上，若给定 I（Nm，Nn）上的一个关系 R，对∀h，k∈I（Nm，Nn），h R k，当且仅当 h，k 在 Nm-1上的限制相同。易证R是一个等价关系。从而R确定I（Nm，Nn）上的一个划分，并将其划分为诸陪集 I（Nm，Nn）/R。这样诸集合ν-1｛φ｝实质上就是诸陪集。当然它们是互不相交的。

又由于 φ 共有 #I（Nm，Nn）=Am-1n多个，所以诸集合ν-1｛φ｝也就有Am-1n个，故由（1）式有

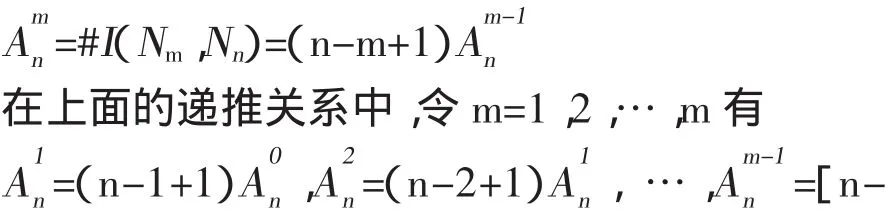
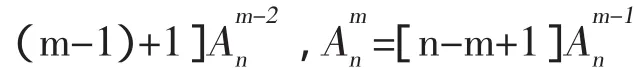
以上各式左右分别相乘，化简得

例2用0～9这十个数字，可以组成多少个没有重复数字的三位数？

我们从如下的角度去考虑，设集合P=｛0，1，2，…，9｝，并视其为具有十个位置的“位置”集合。令A=｛Ⅰ，Ⅱ，Ⅲ｝，其中Ⅰ，Ⅱ，Ⅲ分别表示一个三位数的首位、中位和末位数字。这样，一个三位数就可以视为用A中的元去占有“位置”集合P的三个“位置”。从而，每一个确定的三位数就定义了一个单射f∶A→P，其中f（i），i=Ⅰ、Ⅱ、Ⅲ是在P中被i所占有的位置。因Ⅰ，Ⅱ，Ⅲ中任两个不可能占据同一位置，因而f是一对一的。于是有