撞击流混合器内速度脉动的间歇性分析

张建伟，马彦东，王显旺，宋艳芳

（沈阳化工大学，沈阳 110142）

0 引 言

研究表明，作为一种新型高效的反应、混合设备，撞击流混合器具有促进微观混合和强化相间传递的特点［1－3］，在制取超细粉体方面（如制取超细白炭黑、纳米氧化铝等）有着优于普通搅拌槽混合器的性能［4－5］。作者曾以撞击流混合器流场内的压力波动信号为研究对象，按照不同的非线性分析方法研究了该信号的混沌和分形特性，取得了较好的效果［6－7］；与压力波动信号相比，撞击流混合器内的速度时间序列信号包含了该流场内更多动态信息，是混合器内流体的物理特性、运动特性、流动结构等诸多因素的综合反映。由于混合器流体运动的复杂性，传统的线性分析方法无法深入分析这类复杂信号，因此只能借助于分形等非线性方法进行研究［8－9］。

多重分形分析提供了对不同物理系统的局部奇异性的完整描述，间歇特性是指信号幅度具有的伪周期的突然震动，代表着信号的不规则性，作者结合小波变换模极大值方法，对撞击流混合器速度脉动信号进行多重分形分析，计算其间歇性指数，并与相关流动特性进行关联分析，揭示撞击流混合器中不同位置处流体的运动特性。

1 理论及方法

1.1 小波变换模极大值和多重分形

多重分形描述的是分形几何体在生长过程中不同的层次和特征，用来表示仅用一个取决于整体的特征标度指数所不能完全描述的奇异几率分布的形式，从系统的局部出发来研究其最终的整体性质［10］。根据多重分形的机理［11］，对奇异性测度μ，若用一大小为ξ的盒子Bi（ξ）去覆盖测度支集μ，则其q阶矩的配分函数定义为

其中μi＝μ（Bi（ξ）），式中μi是大小为ξ的盒子的质量，N（ξ）指覆盖的盒子的数量。当ξ→0＋时，配分函数具有以下功率关系

则广义维数：

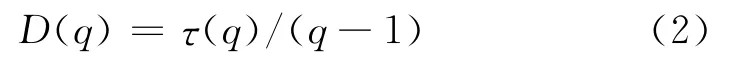
众所周知，小波变换能够实现对信号在时－频两维空间的分解，提供更全面的分析。同时，信号函数的局部行为也可由小波系数反映出来［10－14］。Mallat提出小波变换模的局部极值能够很好地检测出信号的局部奇异性，由此得到由小波变换模极值计算函数空间－尺度配分函数

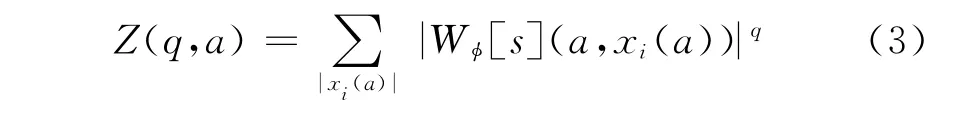
Wφ［s］（a，xi（a））为信号s在尺度a上的小波变换模极大值，即在给定尺度上对其模极大值的绝对值求和。

则配分函数指数由下式得到：

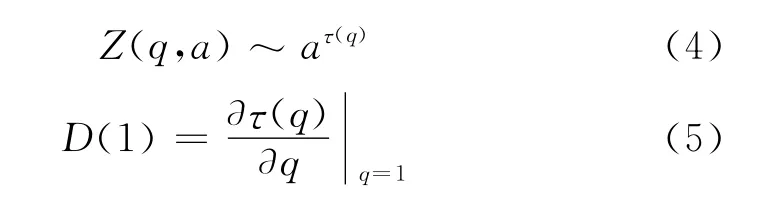
1.2 间歇性指数的确定

间歇性反应了信号的不规则性，其中蕴含着丰富的动力系统信息。由Davis［15］等根据平均时窗的多级倍增串级模型得到表示信号间歇性的度量

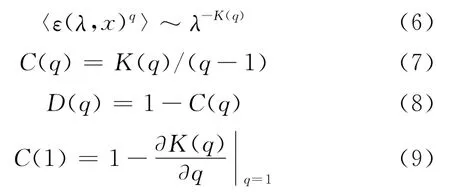
其中D（q）为广义分形维，C（q）为联合维数。一阶维数可作为信号间歇性的定量指标，即C（1）越大间歇性越大，C（1）小则间歇性小。结合式（5）和式（8）则可推出由小波变换模极大值计算的间歇性指数

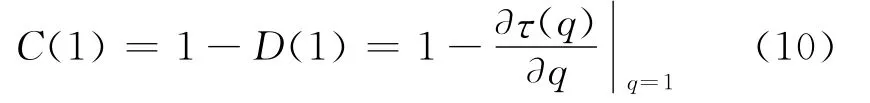
此外，由配分函数指数τ（q）也可判断信号函数的分形特性，若τ（q）为一直线，则信号函数为单分形的，若τ（q）为非线性的，则指数函数是多重分形的。

2 实验测量

实验应用激光多普勒测速系统，撞击流混合器采用浸没循环的工作方式，选取蒸馏水为流体介质，选择密度为1.05～1.15kg／m3、直径为10～15μm的空心玻璃球作为示踪粒子。实验以撞击流混合器两导流筒的轴线中点为原点选取直角坐标系，设水平径向为x轴，导流筒轴线为y轴，垂直径向为z轴。其混合器结构及坐标设置如图1所示。

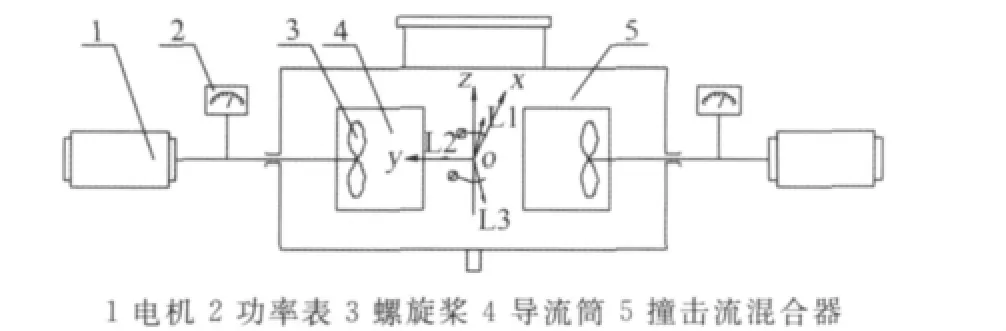
图1 撞击流混合器结构示意及实验坐标设置Fig.1 Schematic structure and coordinate setting of ISM

撞击流混合器设计为轴对称结构，其主体是一个外径为130mm的卧式有机玻璃圆筒，筒内两侧对称安装有两个径长为62mm×72mm的导流筒，间距为72mm；导流筒进口段轴心处各安装有一个轴流推进式螺旋桨；为防止不同频率的激光穿越筒形壁面时发生折射而影响测量精度，混合器外部设置有方型夹套（图中未标示），夹套内注入水以补偿折射的影响［16］。实验测量时，两支螺旋桨分别在转速600，700，800和900r／min下作顺时针旋转，流体在导流筒内被加速，经导流筒出口高速射出，在混合器中心处相向撞击，此后流体转为径向流动，并沿导流筒和环室回流，到达导流筒进口处再次被螺旋桨推送入导流筒。

数据采集时，以坐标原点为分界点，分别在y＝0，±2，±4，±6，±8，±10，±20，±30mm处布置15个测量面，每个面均布168个测点，面内沿x和z方向的点间距设置为4mm。基于混合器的轴对称结构，可选取整个混合器流场的1／4作为测量区域；测量区内每个点的数据采集时间设置为20s，样本最大采样数目设定为20000个。由于速度信号为三维矢量，本实验按照三维激光测速仪的光束设置，分别将速度信号沿正交的X、Y、Z和非正交的L1、L2、L3三个方向进行矢量分解，其中，L2的分解方向与直角坐标系的Y轴同向，L1、L3在XOZ面分别与Z轴的正向和负向呈φ＝6.8°夹角，其示意图如图1所示。

3 结果与分析

3.1 速度信号的分形特征

小波分解系数表示了信号与小波之间的“相似指数”，如果相似程度越高，则相似指数越大。因此如果一个信号的不同尺度之间相似，则小波系数在不同的尺度上也应该相似。因此可以通过小波分解检测信号的自相似性，即检测信号的分形特征。为了清楚地看出速度信号的分形结构，采用效果比较好的连续小波对实验所得瞬时速度信号进行分解，其中信号长度为2000。分解后的尺度图如图2所示。由图2可以看出，该信号具有明显的分形结构，因此可以用分形的观点对其进行研究。

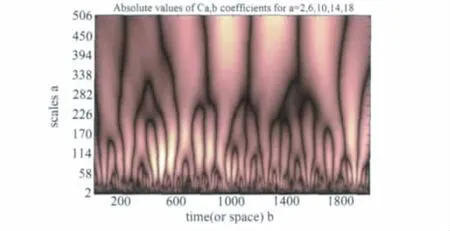
图2 速度信号连续小波分解图Fig.2 Velocity signals decomposed by continuous wavelet

用小波变换模极大值的方法计算不同q值配分函数随尺度a变化的对数关系，由直线斜率可得质量指数τ（q），图3为同一组速度信号计算得出的τ（q）随q值的变化曲线，可见τ（q）为非线性的，所以信号函数为多重分形的，并且信号的间歇性指数C（1）可由q＝1点处曲线斜率及式（10）得到。

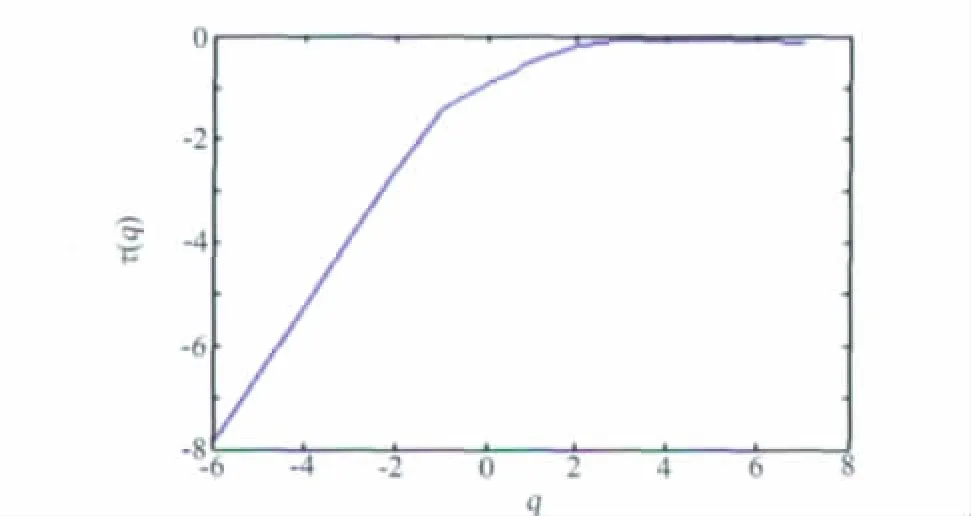
图3 τ（q）随q值的变化曲线Fig.3 Plot ofτ（q）vs q

3.2 小波函数的选择

小波ψ（x）的选择不是唯一的，但它的选择应该满足定义域紧支撑条件和小波容许条件［17］，除此之外，小波函数的消失矩也很重要，在给定尺度a，小波变换模的极大值随着小波函数消失矩的次数增加而线性增加；为减少极大值的数量而又能保证能检测出信号的奇异性，必须尽可能地选择一个最小的消失矩次数而又能保证其能检测出信号的最大奇异性指数。另一方面，消失矩的次数nψ也控制着小波的形状，高的消失矩意味着小波函数ψ（x）随时间位移快速衰减，因此要选择适当的消失矩次数nψ使频率相近的奇异性不相关而能被检测出。具体对比实验如下，对于不同小波在消失矩n＝2，3，4，5进行比较，如图4所示。

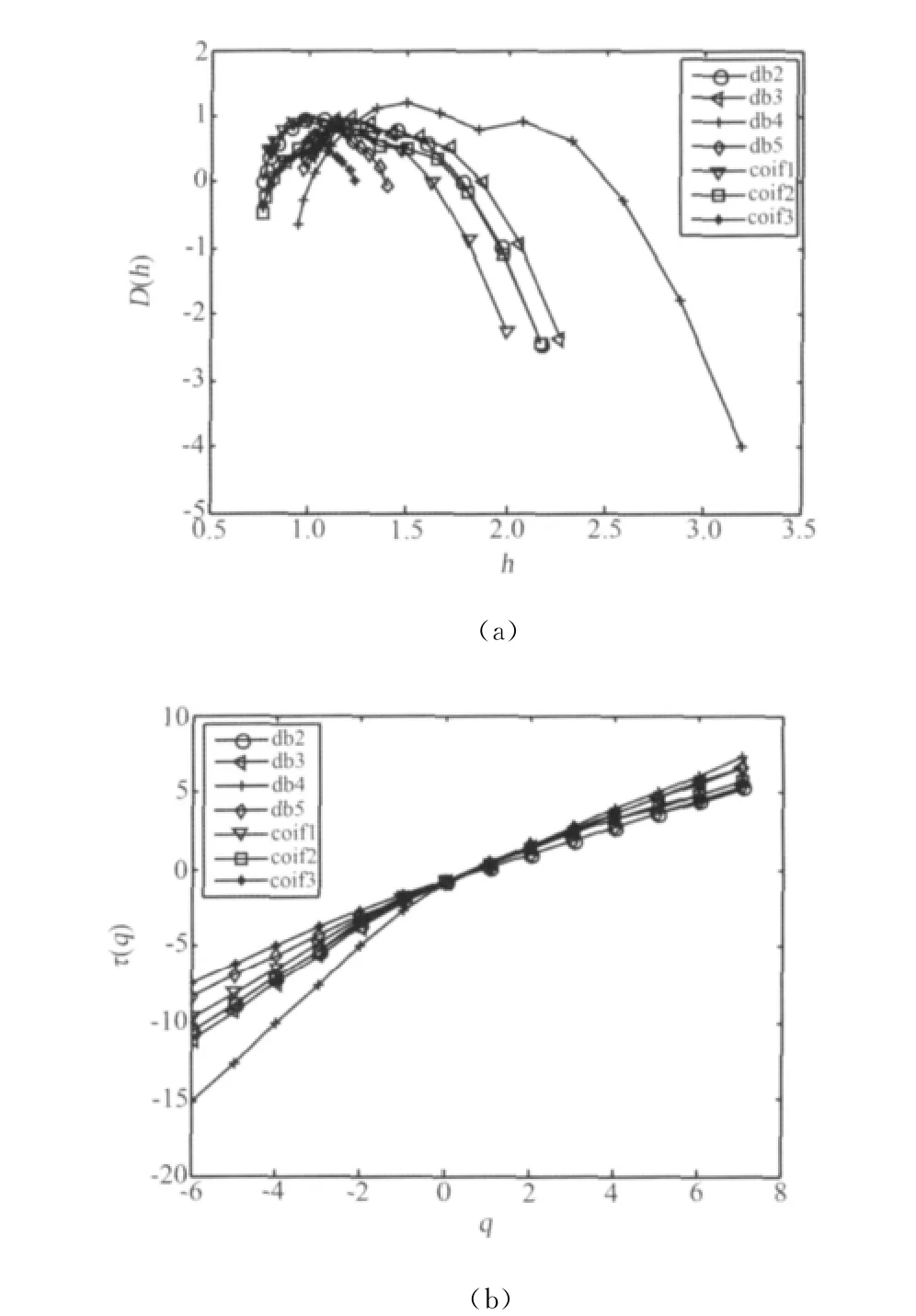
图4 不同小波对比图Fig.4 Comparison of different wavelets

经过计算比较，db4小波函数不仅可以满足算法的条件，节省内存和计算时间，而且，采用db4小波所检测出的奇异谱图形较标准，可以比较真实地反映流体流动的情况。而其它消失矩下的小波函数，都有不同的缺陷，有的不满足判别条件，有的检测不全面，因此选择db4小波。其典型的函数形状见图5。

3.3 同一转速不同位置

根据上述算法，对转速为700r／min时各截面轴向速度和径向速度进行间歇性分析，得到的间歇性指数分别如图6、7所示。

图5 db4的小波函数与尺度函数Fig.5 Chart of wavelet db4and its scale

对于轴向速度分量，由图6可见，y＝0mm截面的间歇性指数沿x轴方向随着远离中心点位置由0.7逐渐增大到0.95，而沿z轴方向基本不受影响，y＝10mm截面的变化趋势与y＝0截面基本一致，只是变化趋势更加缓慢，两截面的间歇性指数位于最大区间，说明两截面间流体撞击剧烈，伪周期振动较多，无序运动占主导地位；y＝20mm截面的间歇性指数突然下降，除个别点外，整个截面几乎位于0.55～0.8之间，说明此区域在远离撞击区的过程中，流体流动趋于平稳。在x＝0～－12mm，z＝－24～－36mm范围内，其间歇性指数达到最低，位于0.45～0.5之间，由于所讨论的范围局限于z＝0～－36mm内，所以可以推断，从z＝－24mm往外的范围内，其间歇性指数会逐渐变小，流体流动更加稳定，符合之前工作中的此区域为回流区的结论。y＝30mm截面的间歇性指数进一步减小，同时在x＝－36mm，z＝－36mm的位置处，间歇性指数也出现了相似于在x＝0～－12mm，z＝－24～－36mm范围内的变化趋势，说明此区域受撞击区影响较小，流体运动规则，形成回流区。上述结论也验证了此前关于撞击流混合器中压力波动的分析结果［18］。

对于径向速度分量，由图7可见，与轴向间歇性指数分布类似，各截面径向速度的间歇性指数呈现相似的分布规律，但是后者在各测量点处的间歇性指数整体上要小于与之对应的轴向分量。在远离导流筒出口的y＝10mm和0mm截面，间歇性指数相对较高，基本位于0.7～0.9之间。在y＝30mm截面除射流区的部分值超过0.8外，其余位置的间歇性指数普遍在0.45～0.8之间上下浮动；由轴向和径向流体的间歇性指数大小可见，轴向流体的高速出射和强烈撞击是造成混合器内复杂的非线性运动的主导原因，相比之下，径向流体仅仅作为一种辅助的手段，它的存在强化了流场的混合强度，并使流场的复杂度分布趋于平均。

3.4 同一位置不同转速

为确定不同的转速对流场间歇性指数大小的影响，取不同转速下直线（X.－10.－32）处各点的间歇性指数值，做曲线如图8所示。整体来看，随着转速的增大，直线上各点的间歇性指数也在不断增大，这在撞击区表现得更明显；n＝900r／min时此区域的间歇性指数几乎全部大于0.85，说明转速的增大提高了该点速度的复杂程度，颗粒之间碰撞加剧，有利于物料的混合。但在靠近回流区的区域，上述规律并不明显。可以认为这主要由于流体的撞击和能量间的转换使得从撞击区回流的流体能量分布趋于均匀，初始速度对系统复杂度的影响已被弱化，因此使得不同转速下的间歇性差异减小，结合上述3.3节的结果得出，此区域的物料将随着速度脉动的放缓而更容易形成聚团，影响混合效果。

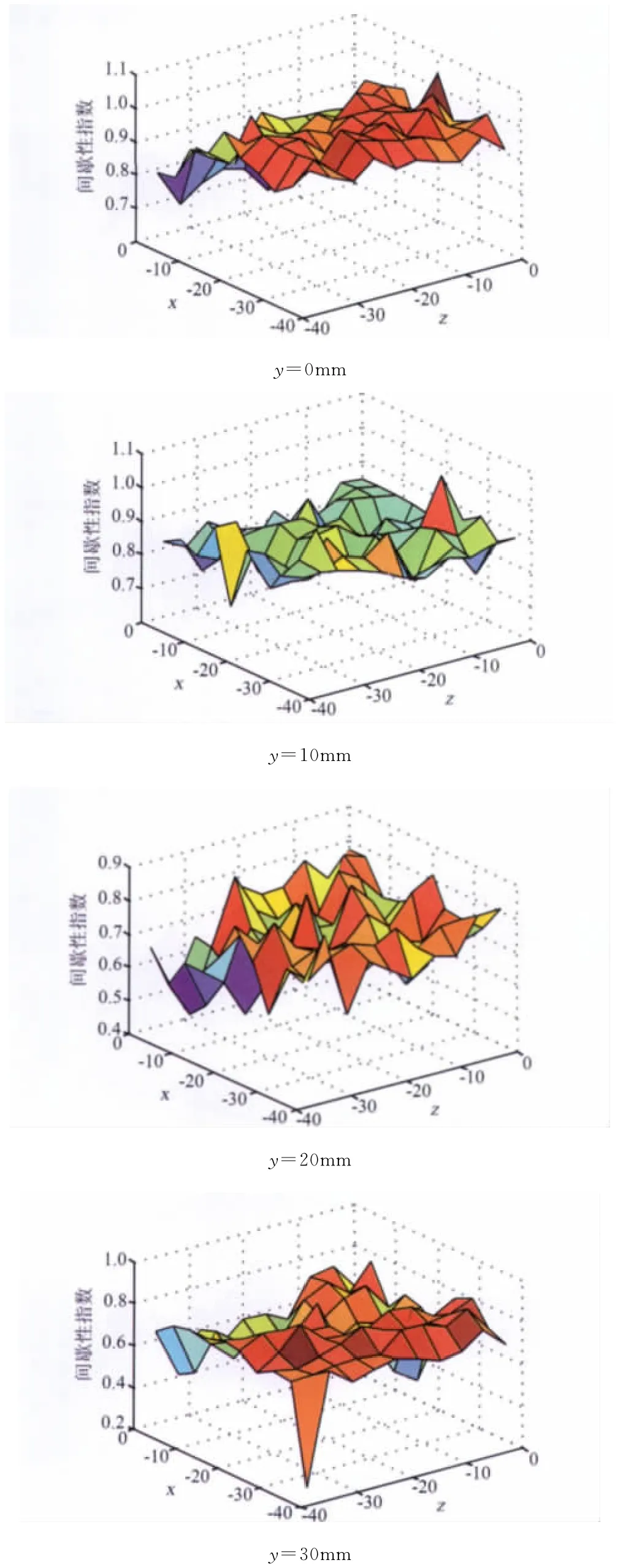
图6 混合器各截面轴向间歇性指数分布Fig.6 Intermittence index on different sections in axis direction

图7 混合器各截面径向间歇性指数分布Fig.7 Intermittence index on different sections in radial direction

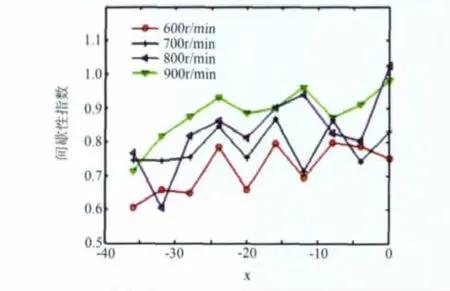
图8 不同转速下（X.－10.－32）处各点的间歇性指数分布Fig.8 Intermittence index on （X.－10.－32）under different rotating speeds

4 结 论

用小波变换模极大值的方法对撞击流混合器内瞬时速度时间序列进行多重分形分析，得到相应的速度脉动间歇性指数。说明撞击流混合器内流体流动具有多重分形的特性；C（1）在不同转速下变化的大体趋势基本一致，但是间歇性指数的大小随转速的不同而有所变化；由间歇性指数随螺旋桨转速的变化得出，增大螺旋桨转速有利于提高系统的复杂度，但在回流区附近，由于流体的撞击和能量转化弱化了初始速度对系统复杂度的影响，转速变化对回流区的间歇性指数影响不大。因此，在撞击流混合器的改进方面，建议适当减小回流区的体积，以减小流体在混合器内的循环周期，更重要的是减少流体逐渐趋于稳定的时间，使流体始终处于较激烈的撞击状态，以达到能量快速转化、混合更加充分的效果。

［1］ 伍沅.撞击流——原理、性质、应用［M］.北京：化学工业出版社，2006.

［2］ 刘海峰，王辅臣，吴韬，等.撞击流反应器内微观混合过程的研究［J］.华东理工大学学报，1999，25（3）：228－232.

［3］ WU Yuan，XIAO Yang，ZHOU Yu－xin.Micromixing in the submerged circulative impinging stream reactor［J］.Chinese Journal of Chemical Engineering，2003，4：420－425.

［4］ 周玉新，程敬华.浸没循环撞击流反应器制备纳米氧化铝的工艺研究［J］.武汉工程大学报，2010，32（5）：1－4.

［5］ 伍沅，陈煜.撞击流反应制取“超细”白炭黑［J］.化工学报，2003，54（10）：1381－1386.

［6］ 张建伟，汪洋，汤慧华，等.浸没循环撞击流反应器撞击区压力波动的混沌分析［J］.化工学报，2005，56（12）：2309－2314.

［7］ 张建伟，焦丽.撞击流反应器压力波动的多尺度多分形特征分析［J］.化工学报，2006，57（7）：1558－1564.

［8］ HALSEY D C，JENSEN M H，KADANOFF L P，et al.Fractal measures and their singularities：the characterization of strange sets［J］.Phys.Rev.A.，1986，33（22）：1141－1151.

［9］ 石志广，周剑雄，赵宏钟，等.海杂波的多重分形特性分析［J］.数据采集与处理，2006，21（2）：168－173.

［10］ ARNEODO A，BACRY E，MUZY J F.The thermodynamics of fractals revisited with wavelets［J］.Physica A，1995，213：232－275.

［11］ 周玉良，陆桂华，吴志勇，等.基于多重分形的降雨时空解集研究［J］.四川大学学报，2010，3（2）：26－33.

［12］ 肯尼思·法尔科内.分形几何中的技巧［M］.曾文曲，王向阳，陆夷，译.沈阳：东北大学出版社，1999：198－240.

［13］ CHHABRA A B，MENEVEAU C，JENSEN R V.Direct determination of thef（α）singularity spectrum and its application to fully developed turbulence［J］.Phys.Rev.A，1989，40（9）：5284－5294.

［14］ 张建伟，焦丽.基于撞击流混合器压力波动信号的小波多重分形奇异谱［J］.过程工程学报，2006，6（4）：627－632.

［15］ DAVIS A，MARSHAK A，WISCOMBE W，et al.Multifractal characterization of nonstationarity and intermittency in geophysical fields simulated［J］.J.Geophys.Res.，1994，99（D4）：8055－8072.

［16］ 崔运静，仇性启，马培勇，等.LDV管道测速实验折射率问题分析［J］.石油化工设备，2005，34（1）：17－19.

［17］ 赵松年，熊小芸.子波变换与子波分析［M］.北京：电子工业出版社，1997：23.

［18］ 张建伟，焦丽，王婷.撞击流反应器内压力波动信号的间歇性分析［J］.石油化工高等学校学报，2006，19（2）：84－88.