电热除冰的热力耦合特性及其对冰层的影响研究

肖春华，林贵平，桂业伟，肖京平

（1.中国空气动力研究与发展中心 空气动力学国家重点实验室，四川 绵阳 621000；2.北京航空航天大学 航空科学与工程学院，北京 100083）

0 引 言

电热除冰过程中，飞机蒙皮表面所结的冰层一方面受到气动力载荷作用，另一方面又受到热载荷的作用。在外部气动力约束下，加热除了融化冰层外，还将在冰层内部产生热应力，这一热力耦合特性是电热除冰过程中的重要特征。

以往的电热除冰计算研究主要围绕除冰结构的传热、冰层融化和冰层的力学特性问题，目前针对电热除冰过程中热力耦合特性的研究还比较少。研究人员［1－6］陆续对电热除冰问题进行了建模和计算，研究了多层电热除冰结构的传热特性和冰层融化特性，但没有考虑加热对冰层力学特性的影响。另外，研究人员［7－10］对气动载荷作用下的冰层内部应力分布进行了计算研究，研究发现低速条件下气动载荷对冰层脱离的贡献不大［9－10］，但研究未考虑加热对冰层力学特性的影响，更没有研究热力耦合特性及其对冰层的破坏影响。因此，很有必要对电热除冰过程中的热力耦合特性及其对冰层的影响进行研究，以预测和掌握冰层的破坏规律以及对冰脱离的贡献。

在电加热条件下，耦合外部气动载荷的作用，采用有限元法研究了电热除冰的热力耦合特性及其对冰层的影响。对加热条件下冰层内部应力的分布特征进行了系统研究，比较了加热和未加热条件下冰层内部应力的差别，研究了热力耦合特性及其对冰层破坏的影响，这对于电热除冰理论和除冰技术的发展都具有现实的意义。

1 数值方法

1.1 计算模型

带冰翼型为NACA0012翼型，表面所结冰型是明冰，外形由文献［11］获得。翼型的前缘局部放大后，得到明冰外形的清晰型线，见图1。冰型外表面受到外部气动载荷作用，内表面受到蒙皮的附着约束作用，当气动载荷导致的冰层应力超过冰层和蒙皮间的抗剪强度时，冰层才可能脱离蒙皮表面。冰层的剥离主要考虑界面应力对冰层和蒙皮间的剪切破坏作用［12］，而冰层的破裂主要依据内部应力对冰层的压缩／拉伸破坏作用，文中的抗压强度取1.0MPa。界面应力分布的横坐标s是沿冰层界面从上表面根部到下表面根部的曲线段长度，加热界面是从弦长s1（0.018m）到s2（0.034m）处，参见图2。

结冰计算条件：来流速度67m／s、压强101300Pa、翼型弦长0.5334m、迎角4°、液态水含量1.0g／m3、水滴平均直径20μm、结冰时间6min、结冰环境温度－6℃。除冰计算条件：来流速度170m／s、环境温度－6℃、加热功率104～4×104W／m2。

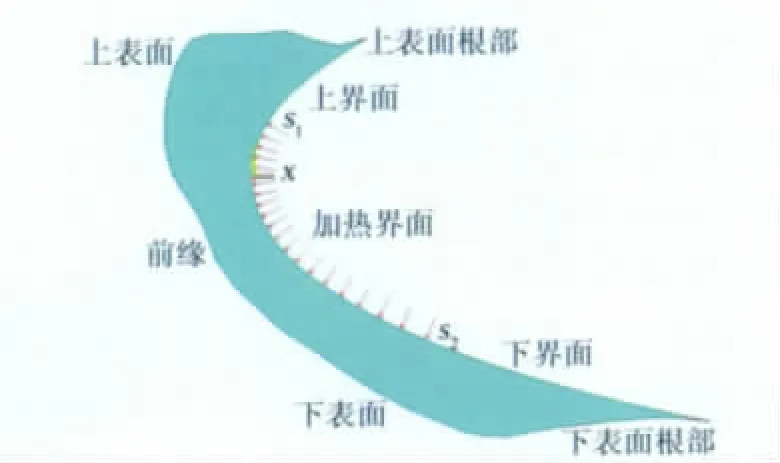
图1 翼型前缘明冰局部放大图Fig.1 Local blowup of glaze ice on airfoil front

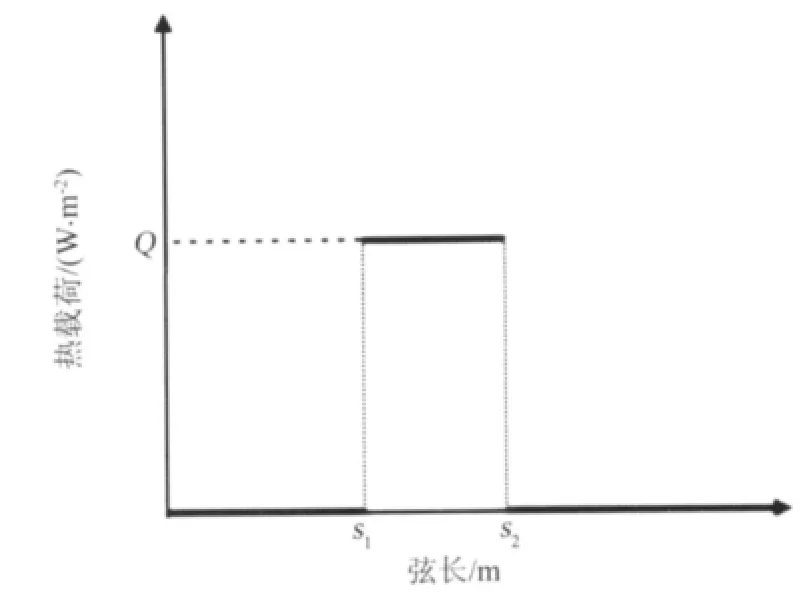
图2 加热界面热载荷分布图Fig.2 Distribution of heat flux at interface

1.2 计算方法

1.2.1 传热问题

（1）控制方程

采用瞬态热传导方程［13－15］

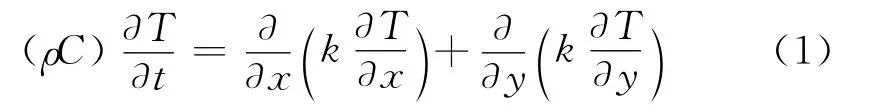
ρ、C、κ分别是冰的密度、比热和导热系数，T是温度。

（2）定解条件

初始条件：取冰的初始温度为T0。

边界条件：参考国外文献［1－6］，在电热除冰过程中，冰层和外流场的交界面一般采用对流换热条件，不考虑继续结冰的情况。其中，是表面单位法向矢量，h是对流换热系数，Ta是环境温度，下标interface代表交界面。

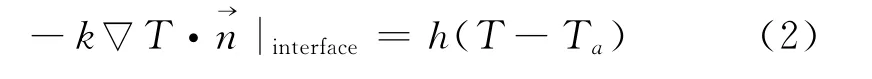
冰层和蒙皮的界面采用恒热流条件，加热界面从弦长s1到s2处的热流密度为Qconst，其它不加热界面采用绝热条件。

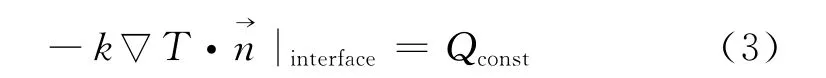
1.2.2 应力问题

（1）控制方程

采用平面弹性力学方程［9］，

平衡方程：

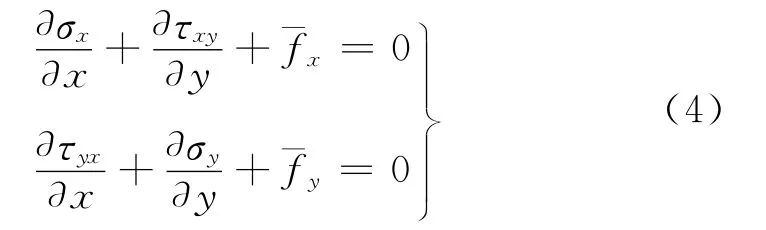
其中，fx、fy分别是x、y方向的单位体积力分量，σx、σy、τxy分别是x、y方向的正应力以及剪切应力。

几何方程——应变－位移关系：

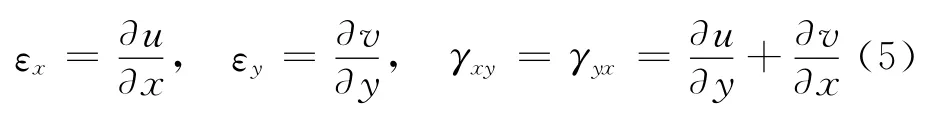
其中εx、εy、γxy分别是x、y方向的正应变及剪应变，u、v是x、y方向位移。

物理方程——应力－应变关系：

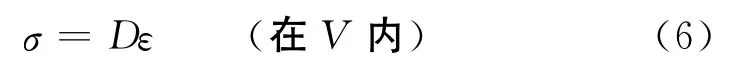
其中，σ是应力向量，ε是应变向量，D是弹性矩阵。

平面应力：E0＝E，v0＝v

（2）定解条件

几何边界条件：

其中，u、v是边界上的位移，、是已知的位移。假定机翼是不发生变形的刚性体，冰层外表面是自由位移条件，冰层和蒙皮间是紧密粘附的无相对位移约束条件，当加热界面的冰层融化变成水，由于水被包围在冰层内，也采用无相对位移约束条件。

力的边界条件：

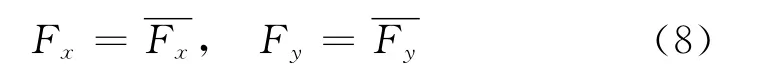
其中，Fx和Fy是边界上单位面积的力和是已知的面积力，这里指流场压力，通过求解低速粘流的时均N－S方程组获得［12］。直接将压力载荷加到冰层外表面每个单元的界面中心，方向沿表面单元的法向。加热界面在融化后只受压不受剪切作用。

对于热力耦合问题，应力计算所需的温度载荷由前面的传热计算获得。

（3）求解方法

为适应冰层不规则的外部形状，应力计算采用有限元法和非结构网格技术，计算单元采用三节点平面应力三角形单元，线性代数方程组采用超松弛迭代法进行求解。冰的物性参数［14］见表1。

表1 冰型的物性参数表Table1 Material properties of the glaze ice

2 计算结果和分析

2.1 界面应力的分布

图3～4是不同热流密度下界面法向、切向应力的分布，加热时间10s。由图可知，随着热流密度的增大，应力变化越来越剧烈。在加热界面附近，热载荷产生的冰层应力非常大，甚至超过了抗拉／压强度，相比之下，气动载荷导致的冰层应力非常小（图3、4中的水平实线），几乎可忽略。加热界面的冰层受热最严重，冰层受热产生膨胀，膨胀受到阻碍产生较大的压应力，所以界面法向应力在加热界面为负，表现为压应力。加热界面两侧受热较少，法向应力为正，表现为拉应力。加热10s时，加热界面的冰层还未融化，此时切向应力在加热界面为正，表现为往上的剪切作用，在加热界面两侧为负，表现为往下的剪切作用；而当加热界面的冰层融化后，切向应力等于零。单位时间冰层受热越厉害，造成加热面及附近区域的温差越大，冰块受热膨胀程度越大，导致该位置的压应力越来越大，应力绝对值随热流密度的增大明显增大，法向应力在加热面附近区域均出现最大应力峰值。

图3 不同热流密度下界面法向应力分布Fig.3 Interface normal stress distribution under different heat fluxes

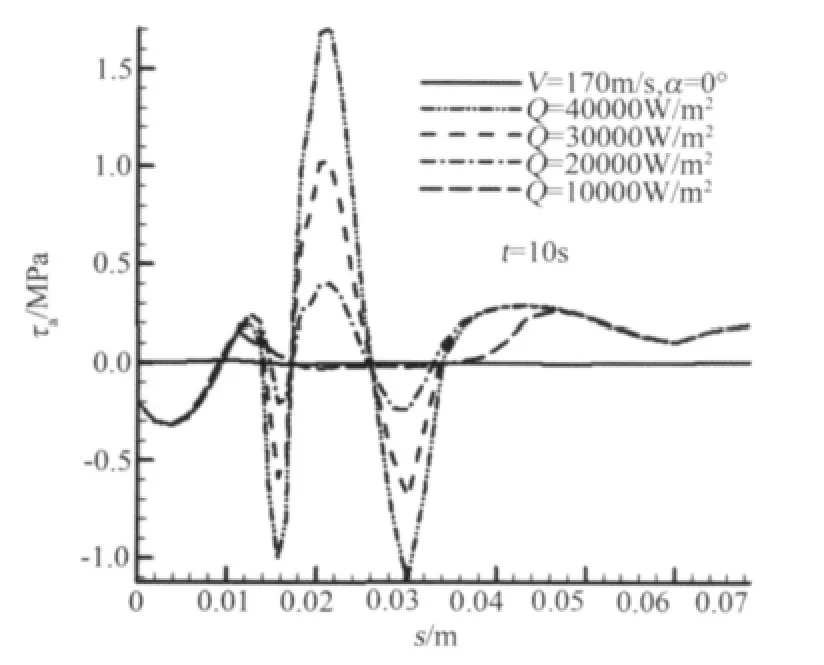
图4 不同热流密度下界面切向应力分布Fig.4 Interface shear stress distribution under different heat fluxes

图中实曲线是热流密度为零也即不加热条件下的界面法向应力和切向应力的分布。可以看出，不加热条件下的界面应力非常小，而加热条件下的界面应力非常大，甚至超过了抗压强度，造成冰层的破坏。所以，在表面冰层融化前，电加热条件下，耦合气动载荷，热力耦合很容易造成冰层的破裂。加热区及附近的冰与翼型界面应力大大超过气动载荷的约束，但由于其它部位的界面应力还没有超过抗压强度，冰与物面间的粘附力仍然存在，所以在一定的加热条件下冰没有发生脱落，而只是发生了局部破裂。

2.2 应力随热流密度的变化

图5是冰层第三主应力最大值随热流密度的变化，加热时间分别为5、10、15和20s。由图可知，相同时间下，冰层第三主应力最大绝对值随热流密度的增加逐渐增大，表现为压应力不断增大。因为热流密度越大，相同时间内冰层的热膨胀就越严重，由于外部气动载荷和界面的约束，膨胀越显著则产生的压应力就越大，导致第三主应力最大值随热流密度的增加而增大。相同热流密度下，第三主应力的绝对值随加热时间不断增大。因为相同热流密度下，加热时间越长，单位时间内传递到冰层的热量就越多，冰层受热就越严重，膨胀也就越显著，所以压应力就越大。图5中多数冰层的最大压应力超过了抗压强度，有的甚至达到4.0MPa，根据破坏条件，预测冰层内部将发生破裂现象。如果冰层具有均匀的物性参数，那么产生最大压应力的部位将率先破裂。当冰层内部发生破裂后，应力得到释放，如果要继续产生破裂，需要进一步加热造成更大的温差，从而产生更大的应力。冰层内部其它部位的应力还未超过抗拉／压强度，所以冰层产生的是局部的破裂而非完全的破碎。

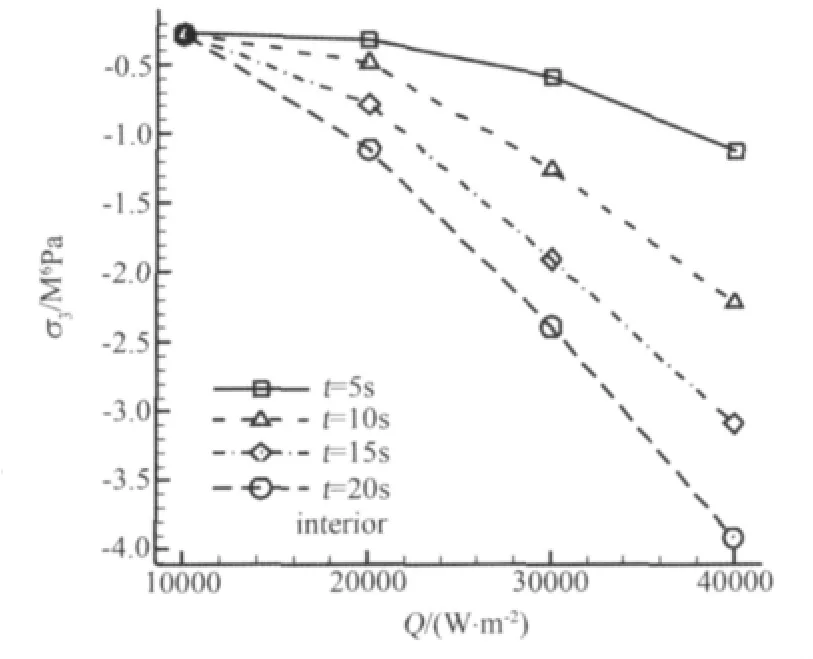
图5 第三主应力最大值随热流变化Fig.5 The third principal stress maximum vs.heat flux

图6是热流密度20kW／m2时冰层内部第三主应力分布云图，加热时间5s。由图可知，在靠近加热界面的区域第三主应力的绝对值最大。随着加热时间的延长，靠近加热界面区域的第三主应力的绝对值越来越大，表现出压应力的不断增大。图7是加热5s时冰层内的温度分布，由图可知，此时冰层内部及界面还未开始融化。

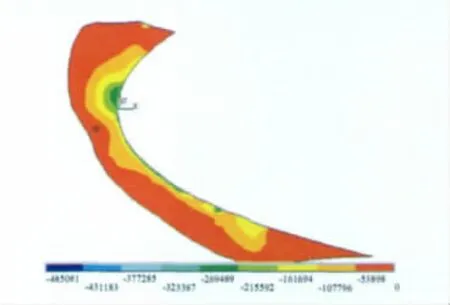
图6 第三主应力分布云图（5s）Fig.6 Contour of the third principal stress（5s）

图7 冰层内部温度分布云图（5s）Fig.7 Contour of temperature in ice（5s）

3 热力耦合对冰层影响的原理性实验

前面的计算表明，在电热除冰过程中，冰层内部将产生很大的应力，局部区域甚至超过了抗压强度，将导致冰层的破裂，为验证结果特进行此原理性实验。实验在气动中心0.3m×0.2m小型结冰风洞中进行（图8），模型采用直径30mm圆柱形电加热装置，共分3层，从外到内依次是硬铝层、中间层和加热层，模型横截面示意图见图9。

图8 结冰风洞第二试验段照片Fig.8 Photo of primary test segment of icing wind tunnel

图9 模型横截面示意图Fig.9 Sketch of model cross section

图10是裂纹出现的时间及相应的表面温度。结冰条件：风速30m／s、结冰控制温度－8℃、结冰时间5min。除冰条件：采用连续性加热模式、电压100V（图10（a））和200V（图10（b））。由图可知，热力耦合将造成冰层的破裂，冰层出现裂纹时表面温度均低于融点，表明裂纹的出现发生在表面冰层融化之前。裂纹出现的时间越早，相应的表面温度就越低。

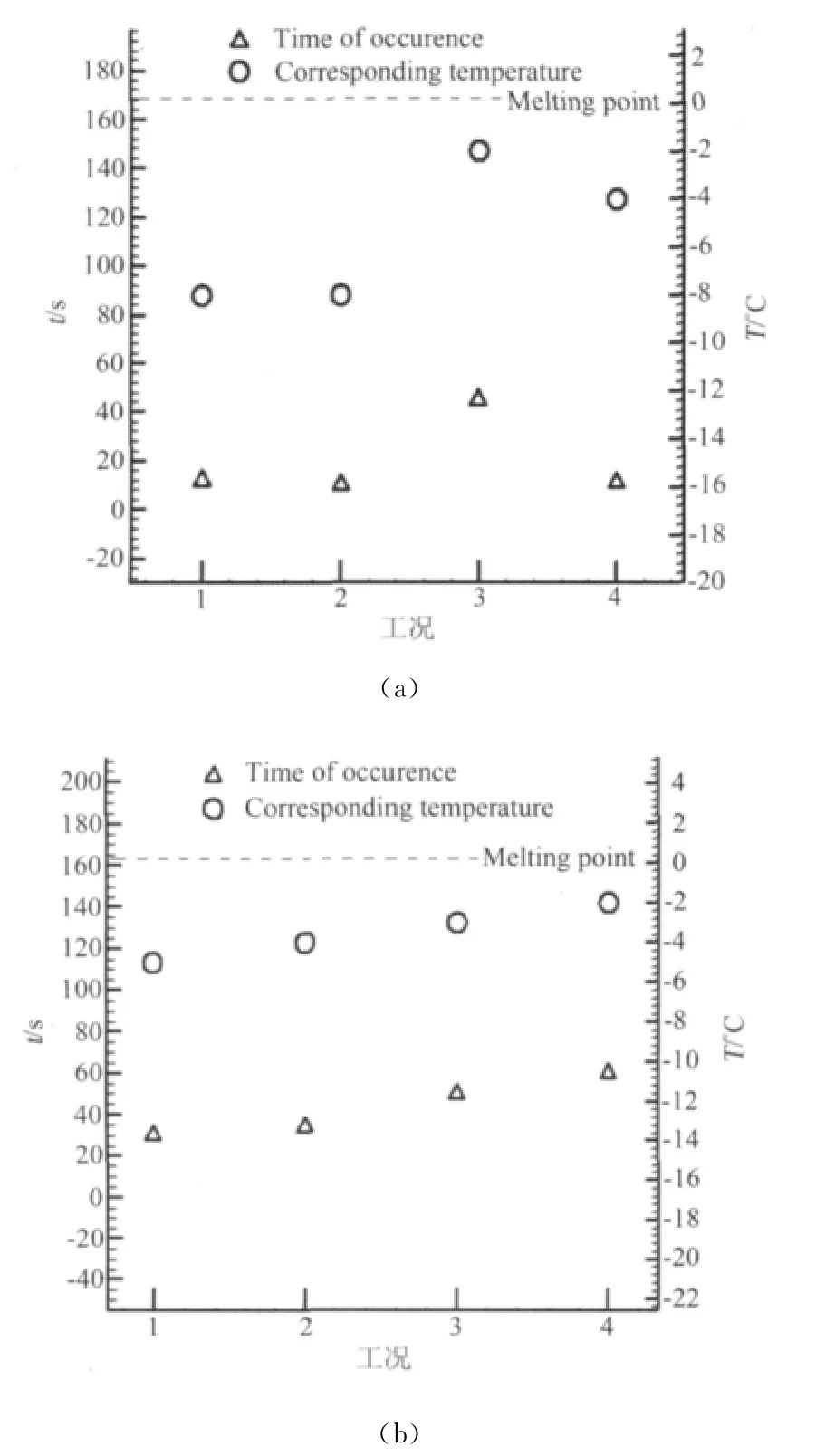
图10 裂纹出现的时间及相应的表面温度Fig.10 Time of crack and temperature of surface

图11是加热前后的冰层比较，包括加热前、加热30s后和加热120s后的冰层。结冰条件：来流风速30m／s、结冰控制温度为－8℃。除冰条件：采用连续性加热模式、电压200V。观察裂纹出现前后的冰层可以发现，表面冰层还没有融化时，裂纹就已经出现了。开启电热除冰装置加热30s后，冰层中下部出现了一条大约3～5cm长的裂纹，裂纹表面的方向和圆柱轴向呈很小的角度，此时的表面温度显示表面冰层还未融化。裂纹出现在表面冰层融化之前，先出现裂纹后发生融化，裂纹是由电热除冰过程中热力耦合产生的冰层内部应力造成的。加热120s后，裂纹有轻微的扩大。随着加热的继续，冰层有时会在主裂纹旁扩展出二次裂纹（图12）。

图11 加热前后的冰层比较Fig.11 Comparison of ice before and after heating

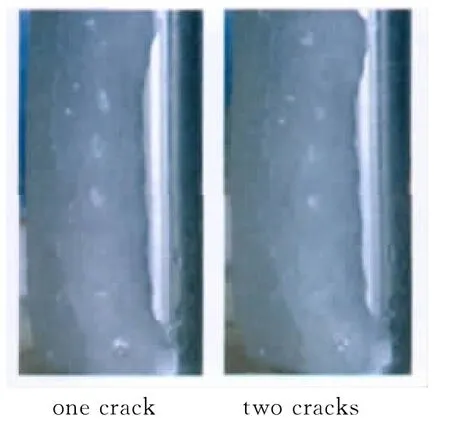
图12 出现主裂纹和二次裂纹的冰层Fig.12 Ice of main crack and two cracks

4 结 论

首先采用有限元法，在电加热条件下，耦合外部气动载荷的作用，对冰层的热力耦合特性进行了计算研究，最后通过原理性实验对热力耦合特性对冰层的影响进行了验证，研究获得如下结论：

（1）热力耦合产生的冰层应力非常大，局部区域明显超出了抗拉／压强度。法向应力在加热界面为负，表现为压应力，而在两侧界面为正，表现为拉应力。随着热流密度的增加，界面应力变化越来越剧烈，界面应力绝对值明显增大；

（2）随着热流密度的增大，冰层受热膨胀的程度越来越大，冰层内部第三主应力的最大绝对值不断增大，表现为不断增大的压应力；

（3）冰层最大压应力明显超过了抗压强度，冰层局部区域将发生破裂，裂纹的出现发生在表面冰层融化之前。冰层发生破裂后，应力得到了释放，随着加热的继续，冰层有时会在主裂纹旁扩展出二次裂纹。冰层其它区域的应力未超过抗拉／压强度，故只产生局部的破裂而非完全的破碎。

［1］ BALIGA G.Numerical simulation of one－dimensional heat transfer in composite bodies with phase change［D］.To－ledo Ohio：University of Toledo，1980.

［2］ CHAO D F.Numerical simulation of two－dimensional heat transfer in composite bodies with application to deicing of aircraft components［D］.Toledo Ohio：University of Toledo，1983.

［3］ LEFFEL K L.A numerical and experimental investigation of electrothermal aircraft deicing［D］.Toledo Ohio：University of Toledo，1986.

［4］ MASIULANIEC K C.A numerical simulation of the full two－dimensional electrothermal de－icer pad［D］.Toledo Ohio：University of Toledo，1987.

［5］ WRIGHT W B，KEITH T G，DeWITT K J.Transient two－dimensional heat transfer through a composite body with application to deicing of aircraft components［R］.AIAA－88－0358，1988.

［6］ YASLIK A D，DEWITT K J，KEITH T G.Further developments in three－dimensional numerical simulation of electrothermal deicing systems［R］.AIAA－92－0528，1992.

［7］ SCAVUZZO R J，CHU M L，KELLACKEY C J.Structural analysis and properties of impact ices accreted on aircraft structures［R］.NASA－CR－198473，1996.

［8］ SCAVUZZO R J，CHU M L，OLSEN W A.Structural properties of impact ices accreted on aircraft structures［R］.NASA－CR－179580，1987.

［9］ SCAVUZZO R J，CHU M L，ANANTHASWAMY V.Influence of aerodynamic forces in ice shedding［J］.Journal of Aircraft，1994，31（3）：526－530.

［10］ 肖春华，桂业伟，易贤，等.结冰翼型表面明冰的压力分布和应力计算［J］.航空动力学报，2009.

［11］ 易贤.飞机积冰的数值计算与积冰试验相似准则研究［D］.四川绵阳：中国空气动力研究与发展中心，2007.

［12］ LYNCH D A III，LUDWICZAK D R.Shear strength analysis of the aluminum／ice adhesive bond［R］.NASACR－107162，1996.

［13］ HUANG J R.Numerical simulation of an electrothermally de－iced aircraft surface using the finite element method［D］.Toledo Ohio：University of Toledo，1993.

［14］ 王勖成，邵敏.有限单元法基本原理和数值方法［M］.北京：清华大学出版社，1997.

［15］ 竹内洋一郎著.热应力［M］.郭廷玮，李安定译.北京：科学出版社，1977.