二维沟槽粗糙槽道内的湍流特性研究
2012-11-15张宇博车得福
张宇博,车得福
(西安交通大学 动力工程多相流国家重点实验室,西安 710049)
0 引 言
粗糙壁面上的湍流流动现象广泛存在于管道系统、流体机械、换热器等工程应用中。粗糙度的存在不仅会对其上的湍流流动产生重要影响,还会改变介质的传热、传质特性。
自从Nikuradse[1]首先对粗糙管内流动展开系统研究以来,湍流界对粗糙壁面上的流动特性研究逐渐开始重视[2-4],但是由于问题的复杂性,许多相关问题还未认识清楚。前人关于粗糙壁面上湍流的研究大都是以二维横向方肋和砂纸作为粗糙元,而关于沟槽型粗糙壁面的湍流研究还少见报道。这种粗糙元对实际工程应用很有价值,不仅在增强传热传质领域得到应用[5],而且沟槽型粗糙度可以更好地模拟流动加速腐蚀过程中产生的粗糙腐蚀产物膜和局部蚀坑形貌[6]。
以二维横向V型沟槽作为粗糙元,利用二维激光多普勒测速技术(LDV)对粗糙壁面矩形槽道内的流动进行了详细测量,并与光滑壁面结果进行对比来说明沟槽型粗糙度对湍流的影响,证实了所采用的沟槽粗糙壁面槽道湍流不符合传统的壁面相似性假设。
1 实验系统及试样
为实验所搭建的小型水洞试验回路主要包括水箱、水泵、流量测量装置、稳流腔、收缩段、流动发展段、试验测量段以及回流腔等几个部分。
试验段为矩形槽道,几何尺寸为1060mm×100mm×20mm。为保证LDV激光光束进入槽道,侧板上开玻璃窗。槽道底板为可拆卸板,以方便更换不同的粗糙板试样。实验采用的粗糙元为横向二维V形沟槽,沟槽结构特性如图1所示。沟槽顶角α为120°,槽深e为0.8mm,槽间距p为6.4mm。

图1 二维沟槽结构示意图Fig.1 Schematic drawing of the two-dimensional groove(side view)
试验槽道内的湍流统计量分布由美国TSI公司生产的9253型三维激光多普勒测速系统(LDV)完成。激光源由Innova70C-5型氩离子激光器提供,最大输出功率达到0.6W,可以满足水介质的需要。测量体直径大约85μm。测量体位置由高精度三维坐标架控制,3个方向的精度都可达到0.01mm。利用高精度微差压计测量试验段的压降。实验过程中由T型热电偶测量工质温度,保证其波动不超过0.5℃。鉴于其良好的跟随性和光学特性,选用空心玻璃球作为示踪粒子,平均粒径为10μm。
对于每个测量工况,首先调节流量使之达到设定值,待流动稳定后,将测量体移至测量位置,测量沿着槽道横展向中心线进行,实现从壁面直到槽道中心的湍流统计量测量。实验中典型的数据率为几十到100Hz,在每个测量点上,采集10000个以上的数据点来计算平均速度和湍流量。对不同流速下采用适当的低频移,以及保持槽道清洁来有效减小测量信号的背景噪声。
测量位置选在距离收缩段出口下游1875mm处(大约100倍槽道高度),这可以充分保证此处流动已充分发展,且不受出口效应的影响。
实验雷诺数范围如表1所示,其中Ucl为槽道中线时均速度,h为槽道半高度,ν为流动介质(水)的运动粘度,Uτ为摩擦速度。
摩擦速度是用于湍流量无量纲化的重要参数,只有准确获得摩擦速度,才能保证湍流量结果的正确分析。利用测得的试验段压降,计算得到摩擦速度。对于光滑壁面,此方法得到的摩擦速度与Blasius公式(Cf=0.079/Re0.25eq)预测结果吻合良好。对于粗糙壁面,利用由压降计算得到的摩擦速度,采用Spalding全壁面律公式[7]对时均速度进行拟合得到虚拟原点和粗糙度函数,该文所有法向坐标都是以虚拟原点为起点。

表1 实验的测试条件Table1 Test conditions for the present channel flow
2 时均速度结果分析
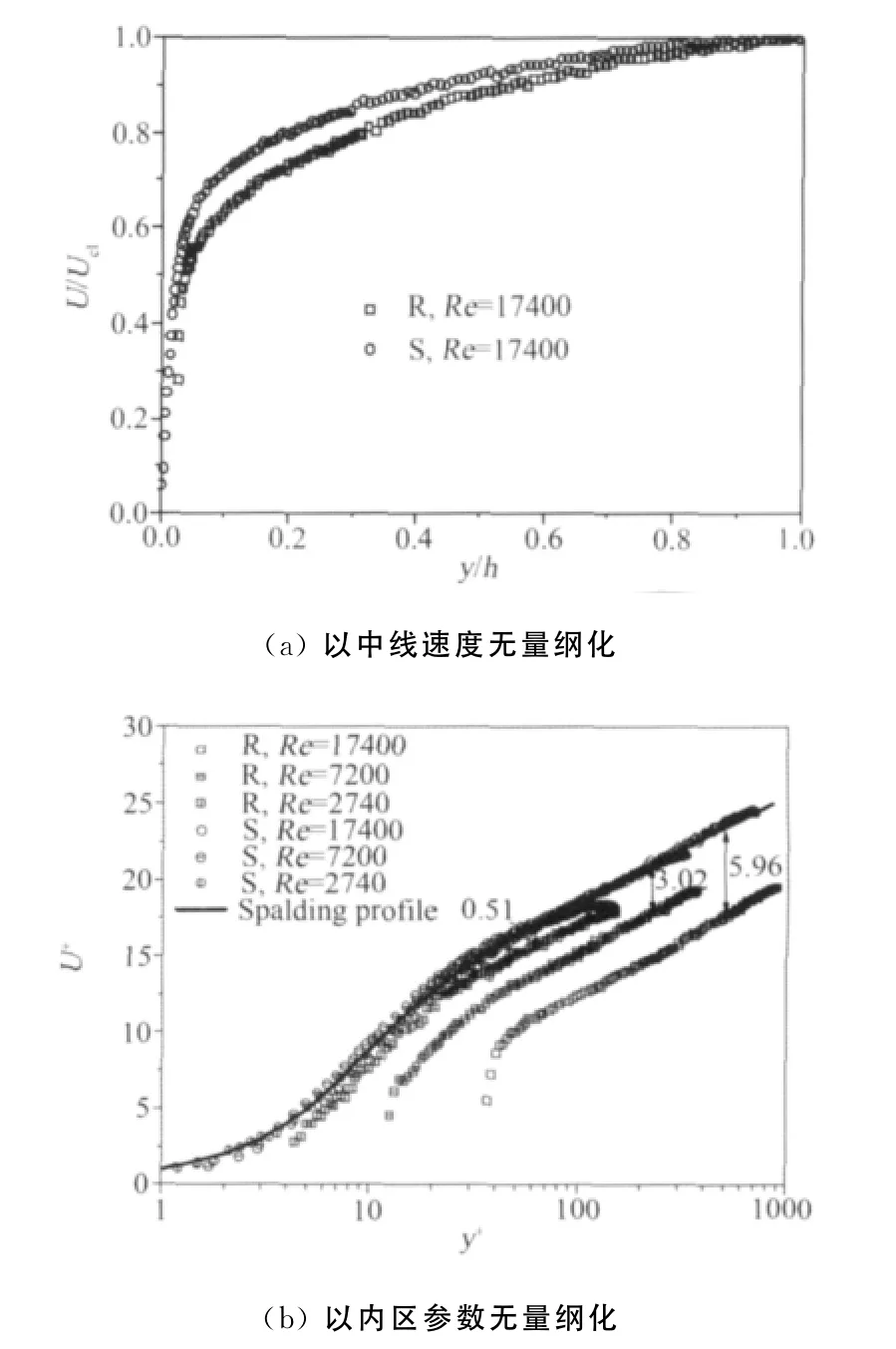
图2 主流方向时均速度分布Fig.2 Streamwise mean velocity profiles across the channel half height normalized by(a)the centerline velocity and(b)the friction velocity and(c)velocity defect profiles
图2给出了主流方向时均速度分布的3种不同无量纲化结果。图中“R”和“S”分别表示粗糙壁面和光滑壁面。由图2(a)可知,由于粗糙度引起更大的阻力,导致时均速度相比光滑壁面减小。当用内区参数来对时均速度进行无量纲化时,粗糙度的影响表现为粗糙度函数。从图2(b)可以看出,各雷诺数工况下光滑壁面上的测量结果与Spalding公式[7]吻合较好。而对粗糙壁面,随着雷诺数的增大,粗糙度函数逐渐增大,由最低雷诺数下的0.51增大到最高雷诺数下的5.96。很多研究认为光滑壁面和粗糙壁面上的速度亏损分布基本一致[8-9],即速度亏损率归一化,而与壁面条件无关。而本实验结果说明在当前雷诺数范围内,不仅光滑壁面和粗糙壁面上的速度亏损分布各自都呈现出随雷诺数增大而升高的趋势,且粗糙壁面结果普遍比光滑壁面高,说明沟槽型粗糙壁面上的时均速度亏损分布不符合归一律,暗示粗糙度的影响不仅局限于内区,这与 Akinlade等[10]及Bhaganagar等[11]的结论一致。
3 二阶量和高阶量结果分析
3.1 湍流强度
图3给出了流向和法向无量纲湍流强度沿槽道高度的分布。许多研究表明,粗糙度对湍流强度的影响主要集中在近壁面区域,如图3(a)所示,沟槽引起近壁面区流向湍流强度最大值显著降低,这可能是由于粗糙度导致流向涡的减弱造成的[12-13]。另外,实验中光滑壁面湍流强度测量结果与文献中直接数值模拟(DNS)[14]结果和 LDV 测量结果[15]吻合良好,证实了测量的可靠性。由图3(b)可知,粗糙度除了引起内区流向湍流强度的减小,还明显增大了外区的湍流强度,这说明当前的粗糙度形式对整个流动边界层都产生了重要影响。法向速度分量的脉动与湍动能在槽道内的传输密切相关,如图3(c)所示,与光滑壁面相比,当前的沟槽粗糙度还导致外区法向湍流强度增大,甚至比流向湍流强度增大更多,说明法向速度分量对壁面条件更为敏感,这可能是由于沟槽的存在使得法向壁面条件改变引起的。外区湍流强度的增大说明粗糙壁面上发生了更强烈的湍流传输。这些发现与前人[13,16]关于二维横向方肋粗糙度的研究结果一致。
图4展示了不同雷诺数下流向湍流强度沿槽道高度的分布。光滑壁面上的湍流强度与Moser等[17]的DNS结果吻合良好,都显示出低雷诺数的影响。与光滑壁面类似,粗糙壁面上的湍流强度在当前测试雷诺数范围也表现出对雷诺数的依赖性,随着雷诺数的增大,湍流强度的最大值逐渐减小且位置不断向壁面靠近,说明雷诺数越大,沟槽对湍流强度的影响也越大。
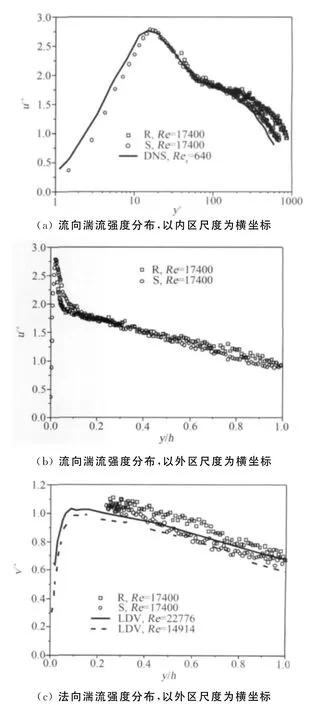
图3 湍流强度分布Fig.3 Normalized turbulence intensity distribution across the channel half height:streamwise component against(a)wall scale and(b)outer-layer scale and(c)wall-normal component
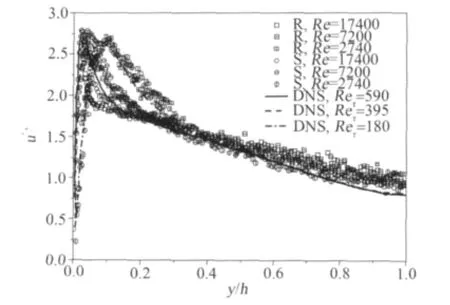
图4 不同雷诺数下光滑和粗糙壁面上流向湍流强度的分布Fig.4 Normalized streamwise turbulence intensity profiles on the smooth and rough walls at different Reynolds numbers
3.2 雷诺切应力
雷诺切应力的测量结果如图5所示。该文的光滑壁面测量结果与文献中的DNS[14]和实验测量[15]结果吻合较好。与光滑壁面相比,粗糙壁面上的雷诺切应力在外区显著增大,再次说明粗糙度对外区的影响不能忽略。
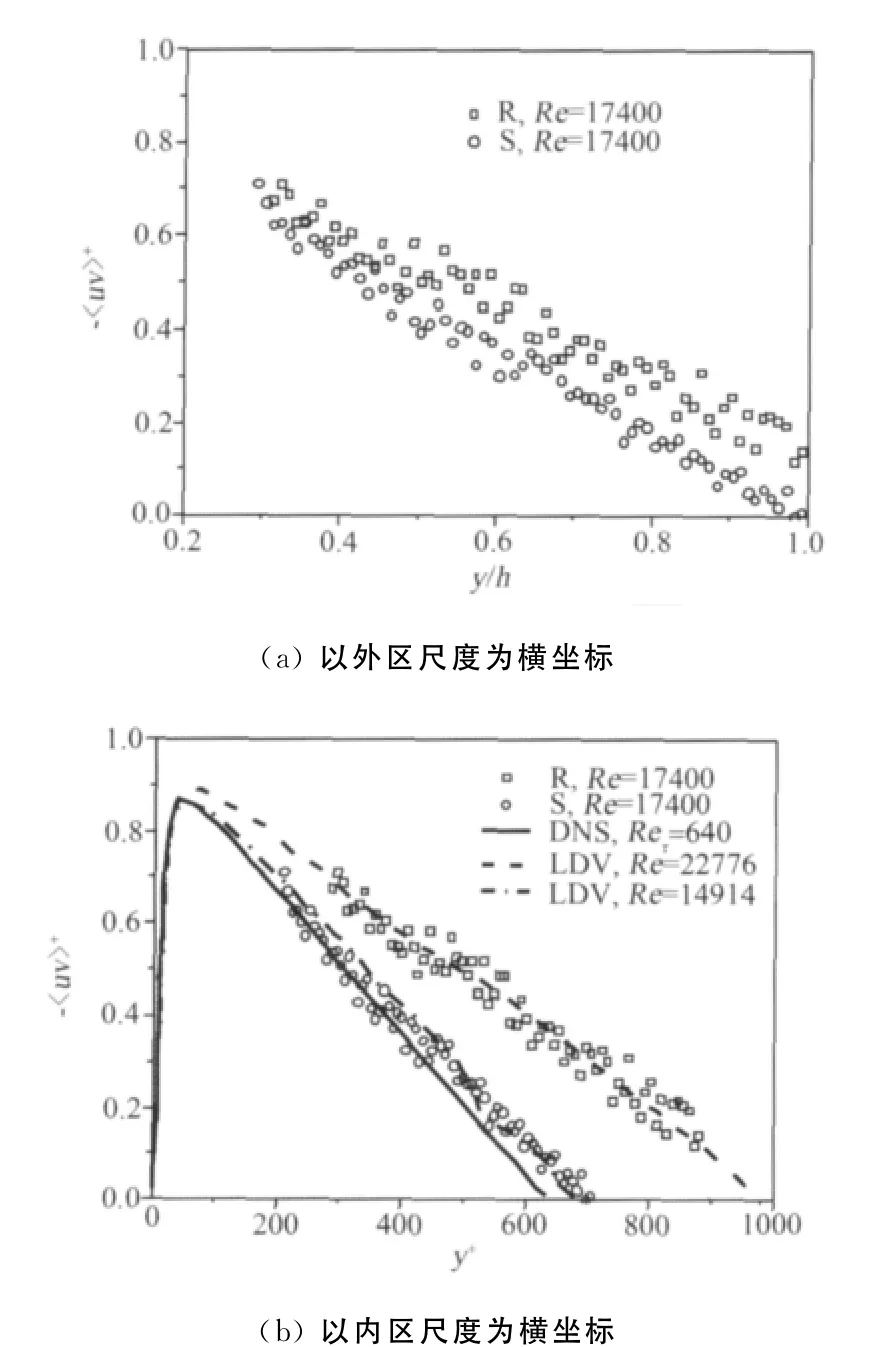
图5 无量纲雷诺切应力在外区的分布Fig.5 Normalized Reynolds shear stress profiles across the channel height against(a)outer-layer scale and(b)wall scale
与流向湍流强度结果类似,雷诺切应力也表现出一定的雷诺数依赖性,随着雷诺数的增大,雷诺切应力不断增大,如图6所示。
3.3 流向脉动速度的偏斜因子和平坦因子
由于高度非线性,脉动速度的高阶矩,即偏斜因子和平坦因子可能对壁面粗糙度更为敏感,因此对评价粗糙度引起的湍流结构及湍流传输过程的变化非常有效。图7给出了流向脉动速度的偏斜因子分布。光滑壁面测量结果与文献[18]基本一致。偏斜因子的符号与湍流“喷发”(ejection)和“下扫”(sweep)事件有关。对于光滑壁面,在近壁面区较高的正偏斜因子说明此处被“下扫”事件控制,而外区负的偏斜因子说明“喷发”事件占主导地位。与光滑壁面相比,粗糙壁面上的偏斜因子相对较大,且由正变负的位置向外区偏移,说明沟槽可能会导致更多的高流速流体冲向壁面的“下扫”过程。
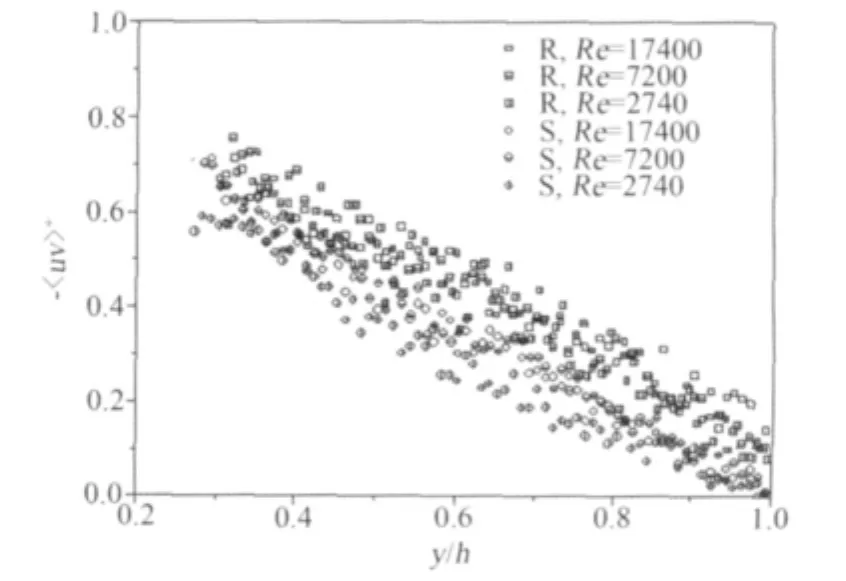
图6 不同雷诺数下光滑和粗糙壁面上雷诺切应力的分布Fig.6 Normalized Reynolds shear stress profiles on the smooth and rough walls at different Reynolds numbers
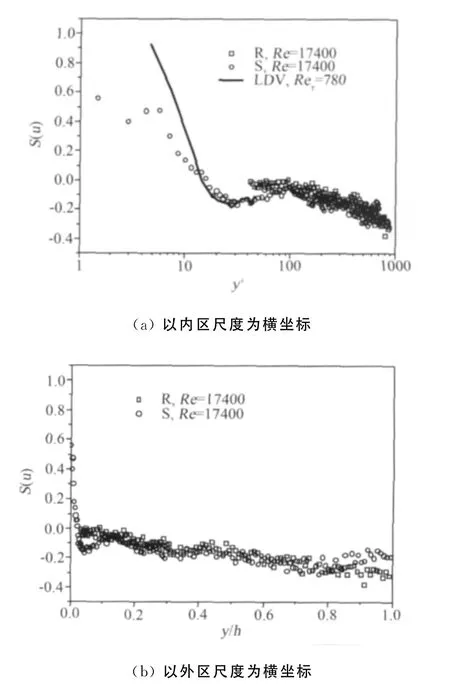
图7 流向脉动速度偏斜因子的分布Fig.7 Streamwise skewness factor distributions across the channel height against(a)wall scale and(b)outer-layer scale
由于测量的难度,四阶矩(平坦因子)在文献中记载的不多。当前光滑壁面的测量结果与Shirai等[18]的近壁面区测量结果吻合较好。除了近壁面区和槽道中心区域,流向平坦因子基本保持在3附近,这与高斯分布相对应。而在近壁面区和槽道中心区域,平坦因子变得较高,说明这些区域湍流的高度间歇性。粗糙壁面与光滑壁面的结果无明显差别。
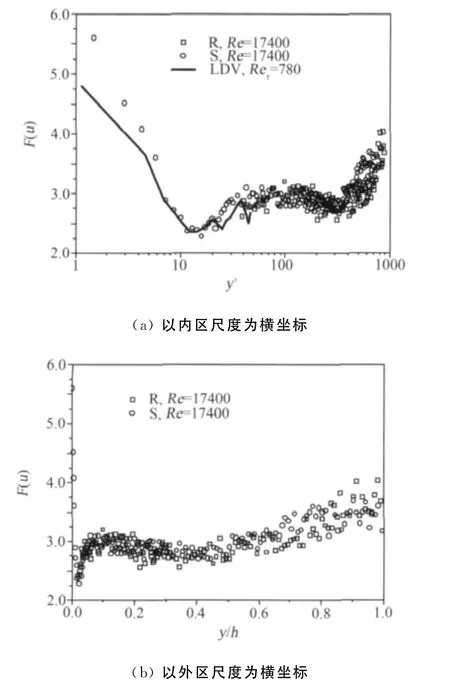
图8 流向脉动速度平坦因子的分布Fig.8 Streamwise flatness factor distributions across the channel height against(a)wall scale and(b)outer-layer scale
4 结 论
利用LDV测量技术,研究了二维沟槽粗糙度对槽道湍流特性的影响,发现与传统壁面相似性假设不同,沟槽型粗糙度的影响延伸到整个边界层范围,而不仅局限于边界层内区。(1)以不同无量纲方式得到的时均速度分布都显示出沟槽粗糙度对整个边界层的影响。粗糙度函数随雷诺数的增大而增大,粗糙壁面上的时均亏损速度高于光滑壁面。(2)内区的湍流强度被沟槽粗糙度抑制而变小,而外区的湍流强度因沟槽变大,且法向湍流强度影响更为明显。外区雷诺切应力因沟槽的引入而变大,并且与湍流强度一样表现出雷诺数依赖性。(3)尽管流向脉动速度的平坦因子几乎不受沟槽的影响,但是对偏斜因子有明显影响,粗糙壁面上更大的偏斜因子说明"下扫"事件对粗糙壁面湍流的重要性。
[1] NIKURADSE J.Laws of flow in rough pipes[M].Technical memorandum 1292,National Advisory Committee for Aeronautics,1933.
[2] JIMENEZ J.Turbulent flows over rough walls[J].Annual Review of Fluid Mechanics,2004,36(1):173-196.
[3] 王晋军,董曾南.加糙平板湍流边界层紊动特性[J].空气动力学学报,1991,9(4):502-508.
[4] 卢浩,王兵,张会强,等.展向不同间距壁面粗糙元对近壁湍流拟序结构的影响[J].实验流体力学,2010,24(05):83-87.
[5] EIAMSA-ARD S,PROMVONGE P.Thermal characteristics of turbulent rib-grooved channel flows[J].International Communications in Heat and Mass Transfer,2009,36(7):705-711.
[6] HAN J,BROWN B N,NESIC S.Investigation of the galvanic mechanism for localized carbon dioxide corrosion propagation using the artificial pit technique[J].Corrosion,2010,66(9):095003-1-12.
[7] SPALDING D B.A single formula for the law of the wall[J].Journal of Applied Mechanics,1961,28:455-458.
[8] RAUPACH M R,ANTONIA R A,RAJAGOPALAN S.Rough-wall turbulent boundary layers[J].Applied Mechanics Reviews,1991,44(1):1-25.
[9] FLACK K A,SCHULTZ M P,SHAPIRO T A.Experimental support for Townsend's Reynolds number similarity hypothesis on rough walls[J].Physics of Fluids,2005,17(3):035102-1-9.
[10] AKINLADE O G,BERGSTROM D J,TACHIE M F,et al.Outer flow scaling of smooth and rough wall turbulent boundary layers[J].Experiments in Fluids,2004,37(4):604-612.
[11] BHAGANAGAR K,KIM J,COLEMAN G.Effect of roughness on wall-bounded turbulence[J].Flow,Turbulence and Combustion,2004,72(2):463-492.
[12] BAKKEN O M,KROGSTAD P A,ASHRAFIAN A,et al.Reynolds number effects in the outer layer of the turbulent flow in a channel with rough walls[J].Physics of Fluids,2005,17(6):065101-1-16.
[13] BURATTINI P,LEONARDI S,ORLANDI P,et al.Comparison between experiments and direct numerical simulations in a channel flow with roughness on one wall[J].Journal of Fluid Mechanics,2008,600:403-426.
[14] ABE H,KAWAMURA H,MATSUO Y.Direct numerical simulation of a fully developed turbulent channel flow with respect to the Reynolds number dependence[J].Journal of Fluids Engineering,2001,123(6):382-393.
[15] WEI T,WILIMARTH W W.Reynolds-number effects on the structure of a turbulent channel flow[J].Journal of Fluid Mechanics,1989,204:57-95.
[16] ANTONIA R A,KROGSTAD P A.Turbulence structure in boundary layers over different types of surface roughness[J].Fluid Dynamics Research,2001,28(2):139-157.
[17] MOSER R D,KIM J,MANSOUR N N.Direct numerical simulation of turbulent channel flow up toReτ=590[J].Physics of Fluids,1999,11:943-945.
[18] SHIRAI K,BAYER C,VOIGT A,et al.Near-wall measurements of turbulence statistics in a fully developed channel flow with a novel laser Doppler velocity profile sensor[J].European Journal of Mechanics BFluids,2008,27:567-578.
