局部扭转形变下典型armchair型石墨烯纳米带的力电特性

鲍正祥, 贾建明

(1.淮安信息职业技术学院 基础教学部, 江苏 淮安 223001； 2.淮阴师范学院 物理与电子电气工程学院， 江苏 淮安 223300)

局部扭转形变下典型armchair型石墨烯纳米带的力电特性

鲍正祥1, 贾建明2

(1.淮安信息职业技术学院 基础教学部, 江苏 淮安 223001； 2.淮阴师范学院 物理与电子电气工程学院， 江苏 淮安 223300)

将密度泛函理论与非平衡格林函数方法相结合,选取了宽度为11根碳原子链、边缘H钝化的armchair型石墨烯纳米带为模型,系统研究了局部扭转形变对石墨烯纳米带力电特性的影响．结果表明,随着扭转角度的增加,armchair型石墨烯纳米带的结构依次经历了弹性形变、塑性形变直至完全断裂．局部扭转形变对armchair型石墨烯纳米带的力电特性有显著影响,表现出了依赖于形变过程的输运谱和伏安特性．

石墨烯纳米带; 扭转形变; 力电特性; 密度泛函理论

0 引言

石墨稀(Graphene),一种由碳原子组成的二维单原子层六角蜂窝状晶格结构,自2004年在高定向石墨上机械剥离成功后[1],受到了科技界的普遍关注[2,3],其独特的结构和物性[4],使其成为未来纳机电系统和光电子器件的重要候选材料．

石墨烯纳米带,即宽度为纳米量级的准一维单层石墨烯条带,不仅继承了石墨烯的诸多优异性能,成为基于石墨烯的纳米器件的基本单元;而且由于横向边界的存在,进一步展现出多元化、可调控的一些新奇特性．随着横向宽度、边缘形状、边界化学修饰、机械形变的不同,石墨烯纳米带的力、电、磁、光等物性也会发生丰富的变化[4]．目前实验上已有刻蚀、切割、底层化学控制、碳纳米管解离等多种方法制备石墨烯纳米带,甚至能够实现尺寸和边缘的可调、可控．在众多石墨烯纳米带中,zigzag型与armchair型是受关注最多的两种结构类别．在不考虑自旋极化的情况下,所有的zigzag型石墨烯纳米带都是金属性的,而armchair型的带隙随着宽度的增加而减小,其带隙呈周期性变化．

由于厚度只有单个原子层,宽度仅为纳米量级,石墨烯纳米带,无论是自由悬浮,还是存在基底,都极易发生扭曲变形．这种结构变化所产生的应变直接影响着石墨烯纳米带的电子结构和各种物性．基于“应变工程”的思想,人们对不同形变条件下应力、应变对石墨烯纳米带物性的影响和调控进行了深入探讨,对相关的现象、规律和机制有了初步的认识．然而,与实验中常见的凸起于二维平面的局部变形相比,已有的理论研究主要集中在平面内石墨烯纳米带拉伸和压缩形变对其物性的影响和控制．

扭转形变是一种基本且典型的力学变形．研究发现,石墨烯纳米带边界在无任何外部原子修饰(即边界碳原子存在未饱和的悬挂键)或当氟原子与边界碳原子结合(即F化)时,纳米带会自发产生明显的扭转变形．新近的实验也观察到,在利用单壁碳纳米管作约束模板,管内生长制备出的石墨烯纳米带也具有螺旋扭转形状．这种准一维结构在三维空间发生的扭转变形,必将影响到石墨烯纳米带的物性．深入细致的理论研究工作不仅有助于揭示其中蕴含的力电耦合机制和规律,而且对石墨烯纳米带在纳米器件中的应用也具有指导意义．

本文以宽度为11根碳原子链、边缘H钝化的armchair型石墨烯纳米带为模型,通过基于第一性原理的量子输运计算,系统研究了局部扭转形变下armchair型石墨烯纳米带的力电特性．结果表明,局部扭转形变对armchair型石墨烯纳米带的形变过程和输运特性有显著影响．

1 理论方法

Armchair型石墨烯纳米带根据其宽度分为三类,即宽度为3p、3p+1和3p+2 (p为正整数)．三种宽度的石墨烯纳米带均属于半导体类型,它们的带隙大小关系为: Δ3p+1≥Δ3p>Δ3p+2(p≠0),armchair型石墨烯纳米带的带隙在总体上随纳米带的宽度的增大而减小[4]．为了深入探讨armchair型石墨烯纳米带在局部扭转形变下的物理特性,我们选取了宽度为11根碳原子链、边缘H钝化的纳米带结构为模型进行了详细考察．

石墨烯纳米带输运性质的计算采用了密度泛函理论与非平衡格林函数方法相结合的框架来进行[5-7]．我们采用了基于Perdew-Zunger交换关联函数的局域密度近似和双ξ极化的数值基组,截断能量为150 Ry,k点取样为1×1×100,原子间相互作用通过Troullier-Martins非局域势来描述．自洽计算的精度为10-5eV．

图1用于研究局部扭转形变下宽度为11根碳原子链的armchair型石墨烯纳米带力电特性的双探针模型示意图．C原子和H原子分别用灰(黑)球和浅灰(白)球表示．

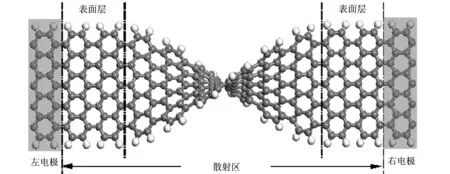
图1 局部扭转形变下armchair型石墨烯纳米带力电特性的双探针模型示意图

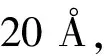
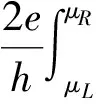
(1)

其中,e是电子电荷,h是普朗克常数,f(E,μ)是Fermi-Dirac分布函数．外加在两端电极的电压V会改变左、右电极的化学势μL=Ef-|e|V/2和μR=Ef+|e|V/2(Ef是费米能,|e|V=μL-μR)．对于处于平衡态(外加电压V=0)的体系,其电导G就是透射系数T(E,V)在费米能级Ef处的值,即:

(2)

2 结果与讨论

图2给出了局部扭转条件下,宽度为11根碳原子链的armchair型石墨烯纳米带在不同扭转角时的结构演化图,灰色区域为扭矩作用区．图2中灰色阴影部分为局部扭转形变中处于表面层和电极区域中扭矩作用下的部分原子．可以看出,在扭转角小于200°时,石墨烯纳米带整体结构依然保持着六角蜂窝状的晶格结构．当扭转角超过200°时,石墨烯纳米带边缘上的C-C结合出现了断键．随着扭转角的进一步增大,断键处的变形愈加明显,直至纳米带完全断开．

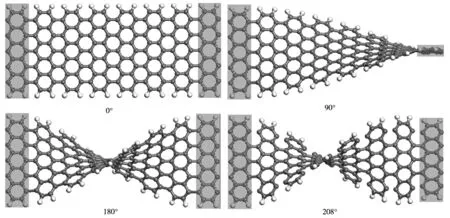
图2 局部扭转条件下armchair型石墨烯纳米带在不同扭转角时的结构演化图

局部扭转时石墨烯纳米带的这些形变特征也可以从应变能曲线中反映出来．纳米带的应变能定义为系统在一定扭转角度下的总能与未发生形变时的总能差,即Es=E(s)-E(0)．图3描述了纳米带的应变能随扭转角的变化趋势．在扭转角小于208°时,中心形变区经历的是弹性形变,此时,扭矩撤销后,石墨烯纳米带能够恢复到初始未形变构型．然而,需要注意的是,弹性形变中石墨烯纳米带的力学行为又可以分为两个阶段:0°～200°时六角蜂窝状结构完整保持下的扭转变形和200°～208°时边缘上的C-C结合出现部分断键下的结构演化．当扭转角超过208°时,发生了无法复原的结构变形(即塑性形变),相应的应变能出现了骤然下降．图3为局部扭转形变下,armchair型石墨烯纳米带的应变能(Strain energy)随扭转角度(Torsion angle)的变化关系．

图4为0电压时不同扭转角度下三种armchair型石墨烯纳米带的输运谱．费米能级设为0 eV．图4给出了不同扭转形变下石墨烯纳米带0电压下的输运谱．很明显,纳米带在费米能级附近有一块0透射区,对应着宽度为11根碳原子链的armchair型石墨烯纳米带的半导体带隙．未发生形变时,输运谱中表现出来的台阶状特征与不同能量下石墨烯纳米带的的电导通道相一致．当发生局部扭转形变后,石墨烯纳米带的输运谱发生了显著变化．值得指出的是,双探针模型中左、右电极区和表面层中的原子除了角度上发生了相对扭转外,它们的结构都和未形变时的情形相同．因此,输运谱的变化完全来自形变区的影响．从图4可以看出,随着扭转角的增加,输运谱的台阶状特征逐渐消失,在很大一个能量区间内的输运谱幅度都在不断减小,其变化原因可以归结为局部扭转形变所产生的散射势垒．为了进一步考察局部扭转形变对armchair型石墨烯纳米带电输运特性的影响,我们计算了不同扭转角度下石墨烯纳米带的伏安特性(I-V),如图5所示．我们以0.1 V为步长,逐渐增大电压．通过纳米带的电流用Landauer-Bottiker公式计算(式1),其中积分区间[uL,uR]对应着偏压窗口．图5为不同扭转角度下armchair型石墨烯纳米带的I-V特性曲线．从图5可以看出,在小电压下,所有不同扭转角度下的石墨烯纳米带中都没有电流．当电压进一步增大时,纳米带中开始出现微弱电流,当电压超过0.4 V后,石墨烯纳米带中的电流迅速增大．这实际上就是armchair型石墨烯纳米带的半导体特性所表现出来的特征．类似的现象在其它半导体纳米结构中也被观察到．

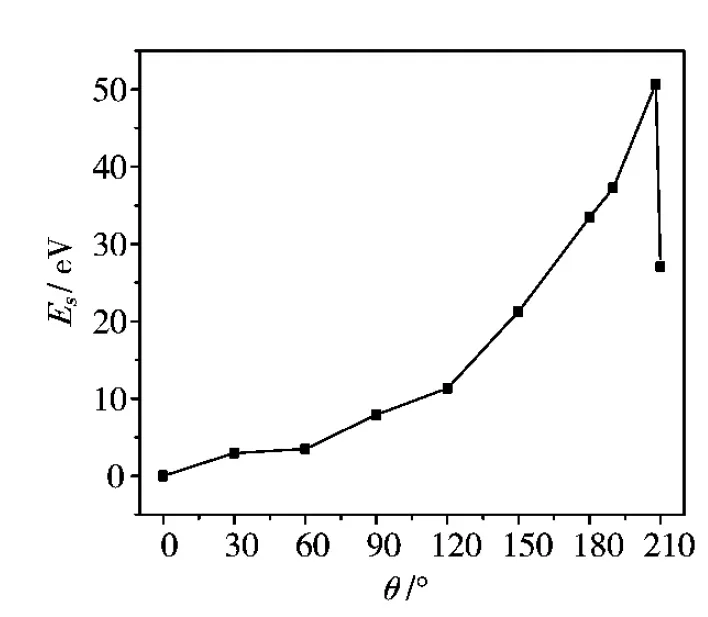
图3 armchair型石墨烯纳米带的应变能随扭转角度的变化关系

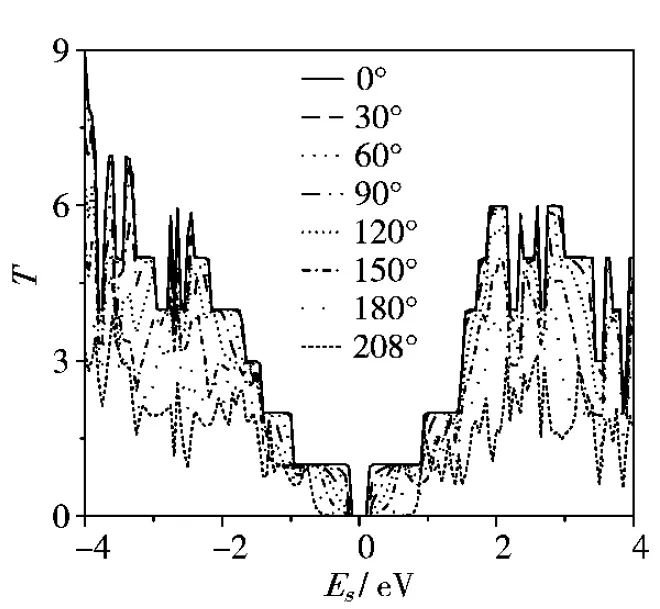
图4 armchair型石墨烯纳米带的输运谱

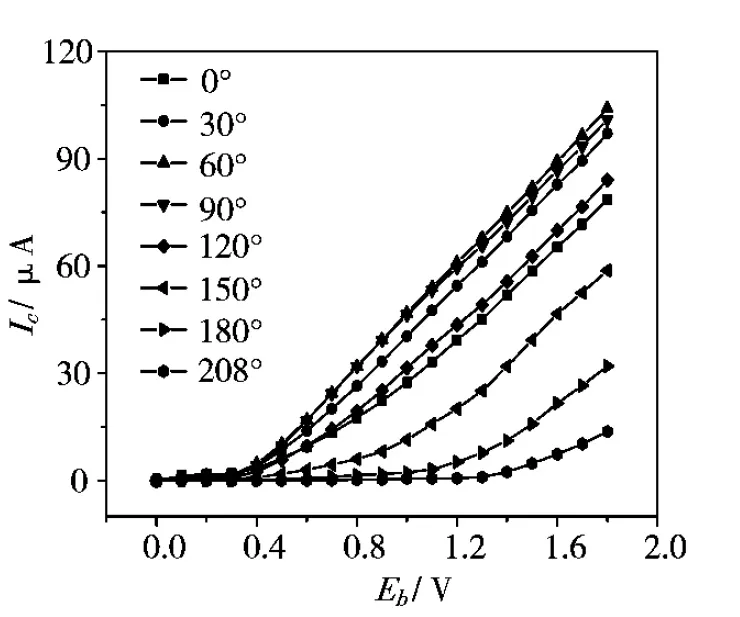
图5 armchair型石墨烯纳米带的I-V特性曲线

从图5中也能看出局部扭转形变对armchair型石墨烯纳米带I-V特性的影响．在同一电压下,通过石墨烯纳米带的电流随着扭转角度的变化而变化．对于宽度为11根碳原子链的纳米带,电流随着扭转角先增大再减小．以未形变时的电流值为参照,当扭转角度从0°逐渐增加到60°时,形变状态下纳米带中的电流不断增大;当扭转角超过60°后,电流随着扭转角的增加又逐渐减小;扭转角小于120°时,纳米带中的电流值依然比未形变时的大;而更大的扭转角度则使得电流大幅下降,到扭转角为208°时,很大一段电压范围内的电流值已趋近于0．纳米管中电流随扭转角度的上升和下降同形变区的电子结构变化是密切相关的．

为了分析其中的机制,我们计算了石墨烯纳米带分别在扭转角为0°，90°和180°时,不同电压下的输运谱. 图6为不同电压和扭转角度下,宽度为11根碳原子链的armchair型石墨烯纳米带的输运谱，费米能级设为0 eV．从图6可以看出,石墨烯纳米带费米能级附近的输运谱随着电压和扭转角度的不同而发生的相应变化,必然会对电流产生直接影响,决定着纳米带中电流的增减变化．

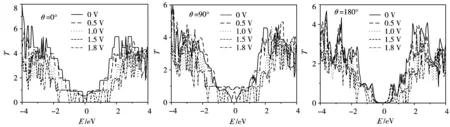
图6 不同电压和扭转角度下armchair型石墨烯纳米带的输运谱

3 结论

采用密度泛函理论与非平衡格林函数相结合的方法,我们通过双探针模型系统研究了局部扭转形变对宽度为11根碳原子链、边缘H钝化的armchair型石墨烯纳米带力电特性的影响．我们观察到,由局部扭转形变所导致的结构变化能够显著改变石墨烯纳米带的输运谱和I-V特性．需要指出的是,尽管我们目前的结果仅是基于特定的宽度为11根碳原子链、边缘H钝化的armchair型石墨烯纳米带计算得到的．但其中所反映出来的半导体型石墨烯纳米带的力电性质及其中蕴含的物理机制则对其它体系也同样适用,并且对石墨烯纳米带在纳机电器件中的应用具有指导意义．

[1] Novoselov K S, Geim A K, Morozov S V, et al. Electric field effect in atomically thin carbon films[J]. Science, 2004, 306(5696): 666-669.

[2] Geim A K. Graphene: status and prospects[J]. Science, 2010, 324(5934):1530-1534.

[3] Sun Y G, Rogers J A. 适用于柔性技术的半导体纳米材料——从光电池学和电子学到传感器和能量存储[M]. 北京:科学出版社,2011.

[4] Castro Neto A H, Guinea F, Peres N M R, et al. The electronic properties of graphene[J]. Rev Mod Phys, 2009, 81(1): 109-162.

[5] Brandbyge M, Mozos J L, Ordejon P, et al. Density-functional method for nonequilibrium electron transport[J]. Phys Rev B, 2002, 65(16): 165401(1-17).

[6] Soler J M, Artacho E, Gale J D, et al. The SIESTA method for ab initio order-N materials simulation[J]. J Phys: Condens Matter, 2002, 14(11): 2745-2779.

[7] Taylor J, Guo H, Wang J. Ab initio modeling of quantum transport properties of molecular electronic devices[J]. Phys Rev B, 2001, 63(24): 245407(1-13).

[8] Delley B. An all-electron numerical method for solving the local density functional for polyatomic molecules[J]. J Chem Phys, 1990, 92(1): 508-517.

[9] Delley B. From molecules to solids with the DMol3approach[J]. J Chem Phys, 2000, 113(18): 7756-7764.

[责任编辑：蒋海龙]

ElectromechanicalResponseofArmchairGrapheneNanoribbonunderLocalTorsionalDeformationNanowires

BAO Zheng-xiang1, JIA Jian-min2

(1.Huaian College of Information Technology, Huaian Jiangsu 223002, China)(2.School of Physical and Electronic Electrical Engineering, Huaiyin Normal University, Huanan Jiangsu 223300, China)

The mechanical and electrical properties of armchair graphene nanoribbon under local torsional deformation have been characterized for the model of armchair graphene nanoribbon with width 11 using a combined formalism of density functional theory and nonequilibrium Green’s function. It is shown that with increasing torsional angle, the deformed region of nanoribbon undergoes the elastic and plastic deformation. The local torsional deformation can have a significant effect on the electromechanical properties of armchair graphene nanoribbon in spite of its semiconducting characteristics, resulting in the torsion-dependent transport spectrum and current-voltage characteristics.

graphene nanoribbon; torsional deformation; electromechanical property; density-functional theory

TP383.1

A

1671-6876(2012)03-0246-05

2012-05-05

鲍正祥(1969-), 男, 江苏淮阴人, 讲师, 硕士, 研究方向为材料物理与器件设计等.