高阶广义正规变化尾的随机游动的大偏差估计

王 丽

(宿迁学院 教师教育系, 江苏 宿迁 223800)

高阶广义正规变化尾的随机游动的大偏差估计

王 丽

(宿迁学院 教师教育系, 江苏 宿迁 223800)

研究高阶广义正规变化条件下随机游动的大偏差估计．假设独立同分布的随机变量的尾分布是高阶广义正规变化函数,得到一个大偏差估计．利用高阶广义正规变化条件的一个等价形式,得到由独立同分布(i.i.d)随机变量生成的随机游动的大偏差Vn(x)=P{Sn>x}的估计．

大偏差; 随机游动; 广义正规变化

0 引言

大偏差理论主要研究罕见事件发生概率的指数型估计,在统计学、偏微分方程动力系统、分形理论、信息论和统计诸学科都有重要和深刻的应用．

文[1]主要研究了正规变化尾的情况下随机游动的大偏差的概率估计,在条件[Dγ],γ∈(0,1)和条件[Dk],k∈Z+下得到了随机游动大偏差的概率估计[1]．但是现实应用的时候尾分布都未必是一阶的正规变化函数,所以本文研究尾分布是高阶广义正规变化尾的情形下随机游动大偏差的概率估计．

设X1,X2,…,Xn是一列独立同分布的(i.i.d)随机变量,具有相同的分布函数F,令

Sn=X1+X2+…+Xn

(1)

则{Sn:n≥1}是由随机变量列{X1,X2,…,Xn,…}生成的随机游动,下面我们记

Vn(x)=P{Sn>x}

(2)

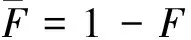
1 高阶广义正规变化条件

定义1[3]设f:R+→R是局部有界的可测函数,如果存在函数a1(t),a2(t)，…,ak(t),h1(x),h2(x),…,hk(x)使得对∀x>0,当t→∞时有

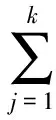
(3)

由定义可以得到如下引理:

引理1[4]如果函数L是一个k阶广义正规变化函数,那么存在函数L1(t),L2(t),…,Lk(t)

使得当y→0,t→+∞时有

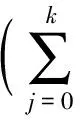
(4)

其中L0(t)=h0(y)=1且

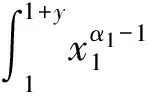
且Lj(t)=o(Lj-1(t)),j=2,3,…，k.

注1[4]若(4)式成立,那么就有

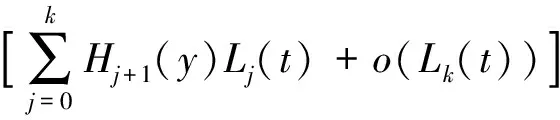
(5)

其中V(t)=P{X1>t}=t-γL(t)∈Rv(-γ),γ>2,即V(t)是指标为-γ正规变化函数

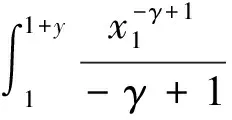
由于Hj+1(x),j=1,2,…,k的表达式是积分形式,表示起来比较麻烦,我们可以利用洛比达(L’Hospital)法则得到它等价形式:

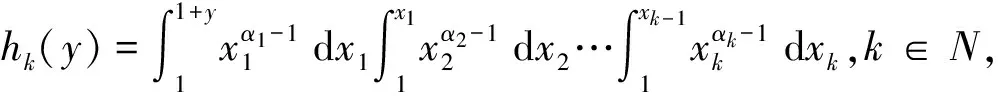
注2[4]利用上述引理, (5)式简化为

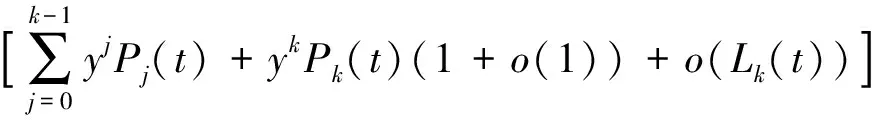
(6)

其中

2 高阶广义正规变化尾的部分和的大偏差估计

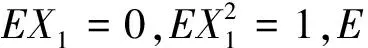
(7)

γ>2,其中Rv(-γ)表示的是甩有指标为-γ的正规变化函数全体[5],这里γ≥d,

由文[1]中的Lemma2可知,在条件(7)下,当x→∞,n≤cx2logx时, 有

Vn(x)=nE[V(x-Sn-1);|Sn-1|<εx]+o(n2x-dV(x))

(8)

于是有以下定理成立:

定理1 如果对于k≤d条件(7)满足且函数L是k阶广义正规变化函数,那么存在常数c>0,当x→∞时,在x→∞,n≤cx2logx上一致时，有

证明用(5)式替代(8)式中的相应部分可得

Vn(x)=nE[V(x-Sn-1);|Sn-1|<εx]+o(n2x-dV(x))=

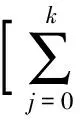
因为对于m≤d,我们有

通过对该疾病的研究,手术治疗为其常用治疗方法,本文就腹腔镜阑尾切除术、开腹阑尾切除术进行对比,发现,开腹阑尾切除术虽然能够彻底切除病灶,但是术后并发症多,切口大,恢复速度缓慢等缺点,整体疗效不甚理想,随着微创技术的不断完善,腹腔镜阑尾切除术逐渐取代开腹阑尾切除术,成为了主要的手术方法,应用价值极高,值得选用[5]。

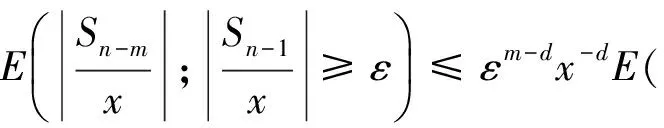
(9)

那么有

(10)

而且对∀j=1,2,…,k,我们有

(11)

那么由(10)和(11)则有

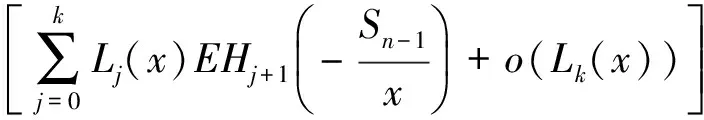
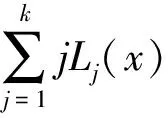
由引理2,我们可以得到Vn(x)的更好的估计如下:

定理2 如果条件(7)对于某些k≤d满足且函数L是k阶广义正规变化函数,那么对于某个常数c>0,在x→∞,n≤cx2logx上一致地有

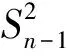
证明用(6)式替代(8)式中相应部分可得

Vn(x)=nE[V(x-Sn-1);|Sn-1|<εx]+o(n2x-dV(x))=

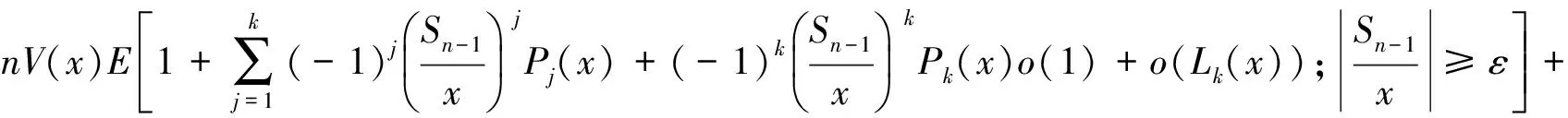
o(n2x-dV(x))

现在(11)式我们有

那么有

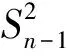
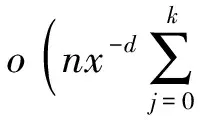
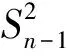
其中

定理得证．

如果计算其中几个Sn的矩可以得到以下推论:

推论1 在定理2的假设下,如果k=2,那么当x→∞时,在n≤cx2/logx上一致地有

推论2 在定理2的假设下,如果d≥k=4,那么当x→∞时,在n≤cx2/logx上一致地有

[1] Borovkov A A, Borovkov K A.On prbabilities of large deviations for random walks with regularly varying distribution tails[J].Theory Prabab Appl, 2001,49(2), 189- 205.

[2] Nagaev S V. Large deviations for sums of independent random variables[J].AnnProbab,1979,7(5),745-789.

[3] Wang X Q, Cheng S H. Genenral regular variation of n-th order and 2nd order edgeworth expansions of the extreme value distribution(I)[J]. Acta Mathematica Sinica,English series,2005,21(5),27- 40.

[4] 季海波,王丽. 高阶广义正规变化尾随机游动最大值的大偏差概率估计[J].徐州师范大学学报:自然科学版,2010,28(2):16- 19.

[5] Binghm N H, Goldie C M, Teugels J L. Regular variation[M].Cambridge UniversityPress, London,etc,1987.

[责任编辑：李春红]

TheEstimationofLargeDeviationofRandomWalkwithHighOrderGeneralRegularVariationTails

WANG Li

(Department of Teacher Education, Suqian College, Suqian Jiangsu 223800, China)

In this paper the estimation of large deviation of random walk with high order general regular variation condition is studied. We propose the tails of independent and identically distributed (i.i.d) random variables have high order general regular variation,and then obtain the estimation of the large deviation probabilities for partial sums. We also use a equivalent condition of high order general variation condition, under the equivalent condition we obtain the estimation ofVn(x)=P{Sn>x}.

large deviation; random walk; general regular variation

O212.62

A

1671-6876(2012)03-0230-05

2011-11-18

王丽(1982-), 女, 山东滨州人, 助教, 硕士, 研究方向为组合设计.