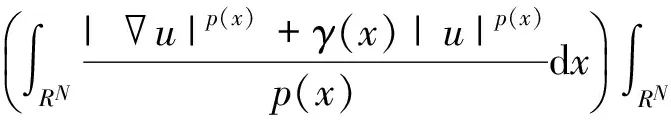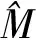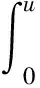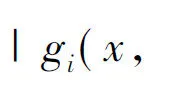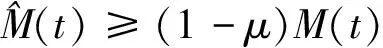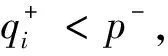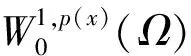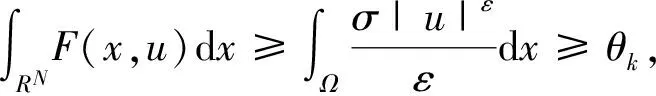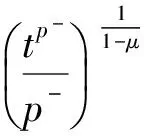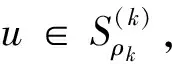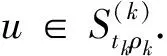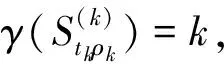一类带奇异系数p(x)-Kirchhoff型问题解的存在性
2012-11-08缪清
缪 清
(云南民族大学 数学与计算机科学学院, 云南 昆明 650500)
一类带奇异系数p(x)-Kirchhoff型问题解的存在性
缪 清
(云南民族大学 数学与计算机科学学院, 云南 昆明 650500)
利用变分方法和变系数的Sobolev空间中的相关定理研究了一类带奇异系数的p(x)-Kirchhoff型问题解的存在性和多解性.
p(x)-Kirchhoff型方程; 广义Lebesgue-Sobolev空间; 存在性
0 引言
本文主要考虑方程
(1)
问题(1)产生于Kirchhoff[6]提出的模型
(2)
关于p-Kirchhoff型的问题已经有了大量的结论[7,8].近期关于p(x)-Kirchhoff问题的研究也有了相应的结论[9].本文受文[4]的启发,研究p(x)-Laplace-Kirchhof型问题解的存在性.本文分为三部分,第二部分主要介绍变系数Sobolev空间中的相关结论.第三部分为问题(1)弱解存在的结论.
1 p(x)-Laplace算子在空间Lp(x)(RN),W1,p(x)(Rn)中的重要性质
为了讨论问题(1),需要用到关于空间Lp(x)(RN),W1,p(x)(Rn)和p(x)-Laplace算子的一些性质.记S(RN)为RN上可测实函数的集合,
h+=esssupx∈RNh(x),h-=essinfx∈RNh(x),h∈S(RN),
h1≪h2即essinfx∈RN(h2(x)-h1(x))>0,
C+(RN)={h|h∈C(RN),h-≥1,x∈RN},
本文假设1 则(Lp(x)(RN),|·|p(x))成为Banach空间,称之为广义Lebesgue空间,并且该空间是可分的自反的[10].定义空间W1,p(x)(RN),如下: W1,p(x)(RN)={u∈Lp(x)(RN)||u|∈Lp(x)(RN)}, 空间W1,p(x)(RN)的范数为 ‖u‖=|u|p(x)+|u|p(x),∀u∈W1,p(x)(RN). 定义 赋予范数 命题1[4]假设a∈Lr(x)(RN),a(x)>0a.e.x∈RN,r(x)∈C+(RN),r->1.如果q(x)∈C(RN)且 记X:=W1,p(x)(RN) 本节主要讨论问题(1)弱解的存在性. 定义1 如果u∈X满足 则称u∈X为(1)的弱解.记: 其中 假设f(x,t)和M(t)满足以下条件: (M0) ∃m0>0使得对所有的t≥0有M(t)≥m0. 命题3[4]Ψ∈C1(X,R)且Ψ,Ψ′是弱强连续的. 如果将问题(1)的能量函数定义为I=Φ(u)-Ψ(u),可以知道I∈C1(X,R)且是弱下半连续的.所以u∈X是问题(1)的弱解当且仅当u是I的临界点.更有甚者, 注1 由(M0)和命题2,Φ′是(S+)型的,由命题3.1,Ψ′是弱强连续的,则I′是(S+)型的. 定义2 称I在X中满足(PS)条件,若任意序列{un}⊂X满足I(un)有界而且当n→∞时有I′(un)→0,有一个收敛的子序列. 引理1 如果M满足(M0),(M1),f满足下面条件: 其中 引理2[4]假设Θ:X→R弱强连续,Θ(0)=0,γ>0是一个给定的常数.令 βk=βk(γ)=sup{Θ(u)|‖u‖≤γ,u∈Zk}, 则βk→0(k→∞). (f2)f(x,-t)=-f(x,t), ∀ (x,t)∈RN×R; (f3) 存在有界开集Ω⊂RN,常数δ,σ,ε>0有F(x,t)≥σtε-1,∀(x,t)∈Ω×(0,σ),1≤ε 则问题(1)存在一列解{±uk,k=1,2,…}使得I(±uk)<0,I(±uk)→(k→∞). 因为I弱下半连续,因此I在X中有极小值点u,u为问题(1)的弱解. 由条件(f2),I是偶函数.因为I在X上是强制的,由引理1,I满足(PS)条件.记γ(A)为A的亏格,令 ck=infx∈Rksupu∈AI(u),k=1,2,…, 当t>t0,由(M1)可以计算得到 其中t0为任意的正常数. 致谢: 本文由云南民族大学青年基金项目资助(11QN10), 在此表示感谢! [1] Fan X L, Zhang Q H. Existence of solutions forp(x)-Laplacian Dirichlet Problem[J]. Nonlinear Anal, 2003, 52: 1843-1852. [2] Fan X L, Han X Y. Existence and multiplicity of solutions forp(x)-Laplacian equations inRN[J]. Nonlinear Anal, 2004, 59: 173-188. [3] Zhang Q H. Existence of radial solutions forp(x)-Laplacian equtions inRN[J]. J Math Anal Appl, 2006, 315: 506-516. [4] Zhang Q H. Existence of solutions forp(x)-Laplacian equations with singular co efficients inRN[J]. J Math Anal Appl, 2008, 348: 38-50. [5] Fan X L. Solutions forp(x)-Laplacian Dirichlet problems with singular coefficients[J]. J Math Anal Appl, 2005, 312: 464-477. [6] Kirchhoff G. Mechanik[M]. Teubner, Leipzig, 1883. [7] Correa F J S A, Figueiredo G M. On a elliptic equation of p-Kirchhooff type via variational methods[J]. Bull Austral Math Soc, 2006, 74: 263-277. [8] Liu D. On ap-Kirchhooff equation via Fountain Theorem and Dual Fountain Theorem[J]. Nonlinear Anal, 2010, 72: 302-308. [9] Dai G, Hao R. Existence of solutions for ap(x)-Kirchhoff-type equation[J]. J Math Anal Appl, 2009, 359: 275-284. [10] Fan X L, Zhao D. On the spaces Lp(x)(Ω)and Wm,p(x)(Ω)[J]. J Math Anal Appl, 2001, 263: 424-446. [责任编辑:李春红] ExistenceofSolutionsforp(x)-KirchhoffTypeEquationswithSingularCoefficientsinRN MIAO Qing (School of Mathematics and Computer Science, Yunnan Nationality University, Kunming Yunnan 650500, China) In this paper, we study the existence of infinite solutions to thep(x)-Kirchhofftype equations with singular coefficients inRN. By means of a direct variational approach and the theory of the variable exponent Sobolev spaces, we establish conditions ensuring the existence and multiplicity of solutions for the problem. p(x)-kirchhoff type equations; generalized Lebesgue-sobolev spaces; existence O175.6 A 1671-6876(2012)03-0221-05 2012-03-02 缪清(1984-), 女, 云南马龙人, 讲师, 博士, 研究方向为偏微分方程及应用.
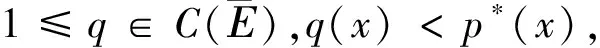
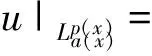
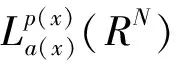
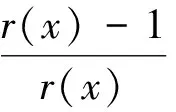
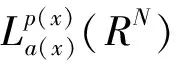
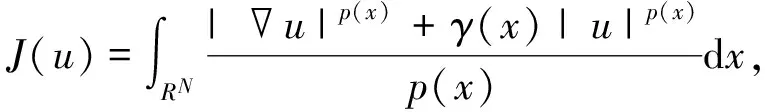

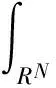

2 解的存在性