含参量曲线积分

吴以立, 王晓晶

(淮阴师范学院 数学科学学院, 江苏 淮安 223300)

含参量曲线积分

吴以立, 王晓晶

(淮阴师范学院 数学科学学院, 江苏 淮安 223300)

在含参量正常积分的基础上给出了含参量曲线积分的概念、性质,主要给出了含参量曲线积分可积的充要条件、含参量曲线积分的连续性、可微性、可积性,以及含参量曲线积分与三重积分可交换的条件.

含参量曲线积分; 连续性; 可积性

0 引言

许绍溥等[1-2]给出了含参量积分的概念、性质,以及含参量积分的连续性、可积性、可微性.于兴江[3]讨论了含参量曲面积分的概念、性质,以及含参量曲面积分的连续性、可积性、可微性.赵清理[4]等讨论了无穷曲线上的积分及其性质.受文[3-4]的启发,本文给出了含参量曲线积分的概念:

定义1(含参量曲线积分的定义) 设U⊂R3,V⊂R3均为三维区域,D=U×V⊂R6为六维区域,函数f(x,y,z,u,v,w)在D上连续且有定义,设L是U内的光滑曲线,若(u,v,w)∈V时,函数f(x,y,z,u,v,w)在L上可积,则称此积分为含参量曲线积分,记为

接着又讨论了含参量曲线积分的性质,主要得到了含参量曲线积分可积的充要条件、含参量曲线积分的连续性、可积性、可微性,以及含参量曲线积分与三重积分的可交换条件.

1 性质

类似于含参量正常积分和含参量反常积分,我们很容易推导出含参量曲线积分的一些基本性质.

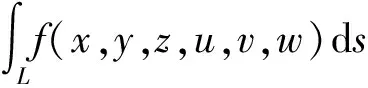
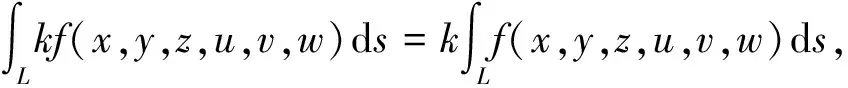
即

其次我们证明

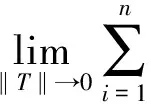
即

综合以上,性质1立即得证.

则当‖T‖→0时有‖Ti‖→0,且有

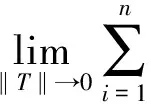
从而性质2得证.

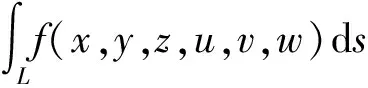
证明由于在D=U×V上

f(x,y,z,u,v,w)≤g(x,y,z,u,v,w),

从而对L的任意分割T总有

令‖T‖→0得

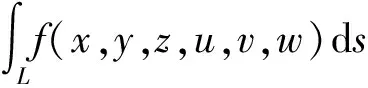
证明利用性质3,性质4可以类似证明.

2 主要结果

类似于有界函数在闭区间上可积的充要条件,我们给出含参量曲线积分在三维闭区域上可积的充要条件.

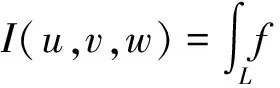
(1)

证明类似于定积分我们可以平行的引入达布下和与达布上和,从而很容易给出定理1的证明.

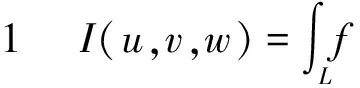
证明对V′的任意分割,以它的全部分点作为V的分点的一部分,并对剩下的区域随意的插入分点,这样就产生了V的一个分割.由定理1及I(u,v,w)在V上可积知条件(1)在V满足,则它在V′也满足.再次利用定理1我们就完成了推论1的证明.

以下我们主要讨论含参量曲线积分的连续性、可积性、可微性.

定理2(连续性) 设U⊂R3,V⊂R3均为有界闭域,L是U内可求长的光滑曲线,若函数f(x,y,z,u,v,w)在有界闭域D=U×V上连续,则函数

在V上连续,即

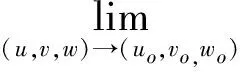
证明任取V内一点P0(u0,v0,w0),对于(u0+Δu,v0+Δv,w0+Δw)∈V(若P0为V的边界点，仅考虑Δu,Δv,Δw大于或小于0),由于f(x,y,z,u,v,w)在有界闭域D上连续,从而一致连续,即

∀ε>0,∃δ>0,∀P1,P2∈D,当ρ(P1,P2)<δ时,有|f(P1)-f(P2)|<ε.

设曲线L的长度为c,则∀(x,y,z)∈U,当|Δu|<δ,|Δv|<δ,|Δw|<δ时,有

|I(u0+ Δu,v0+Δv,w0+Δw)-I(u0,v0,w0)|=

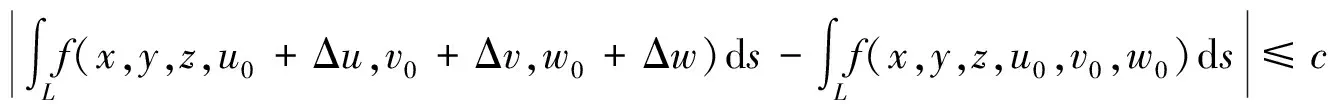
即I(u,v,w)在V上连续.

其中

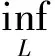
证明对于L的任意分割T,由于

令‖T‖→0,我们有

由定理2及介质定理知存在常数c(u,v,w),使

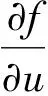
在V上可微,且

证明(我们只证第一个式子,其它两个类似可证) 对于V中任意一点p(u,v,w),设Q(u+Δu,v,w)∈V(若P为V的边界点,则讨论单侧偏导数),

于是

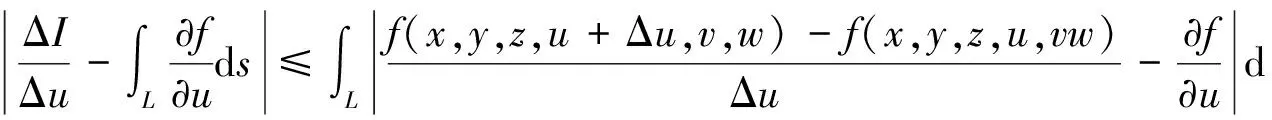
其中θ∈(0,1).于是

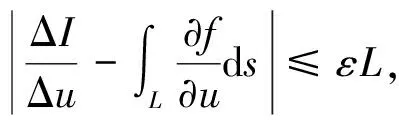
同理可以证明

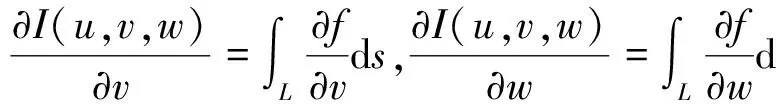
由三个偏导数存在且连续知I(u,v,w)在V上可微.

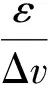
从而由定理1知I(u,v,w)在V上可积.

接下来我们考虑含参量曲线积分与三重积分的可交换性.

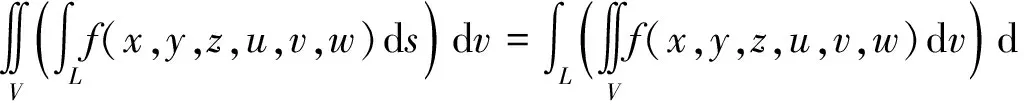
证明对L作分割T1:L1,L2,…,Ln,设其细度为‖T1‖,对V作分割T2:V1,V2,…,Vm,设其细度为‖T2‖,∀(uj,vj,wj)∈Vj,设函数f(x,y,z,u,v,w)在Li×Vj上的上,下确界分别为Mij,mij(i=1,2,…,n;j=1,2,…,m),再设Li的长度为ΔLi,Vj的体积为ΔVj,所以∀(xi,yi,zi)∈Li,都有mijΔLi≤f(xi,yi,zi,uj,vj,wj)ΔLi≤MijΔLi,对上式两端关于i求和得

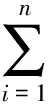
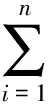
即

对上式两端关于j求和得

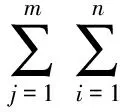
(2)

类似可证

(3)

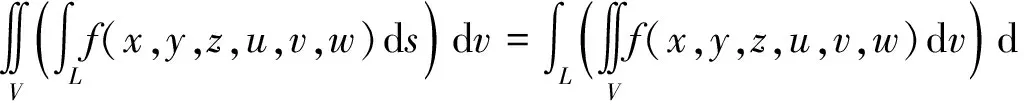
从而我们完成了定理6的证明.

[1] 许绍溥,将东平,宋国柱. 数学分析:上册[M].南京: 南京大学出版社,1991,332-339.

[2] 许绍溥,将东平,宋国柱.数学分析:下册[M].南京: 南京大学出版社,1991,133-158.

[3] 于兴江.含参量曲面积分[J].聊城大学学报:自然科学版,2006,6,19(2):21-24.

[4] 赵清理,于兴江,冷学斌. 无穷曲线的积分及其性质[J].聊城师范学院学报:自然科学版,1999, (3):68-71.

[责任编辑：李春红]

CurvilinearIntegralsContainingParameter

WU Yi-li, WANG Xiao-jing

(School of Mathematical Sciences, Huaiyin Normal University, Huaian Jiangsu 223001, China)

Based on the normal integral Containing Parameter, we gave the concept, characterization, necessary and sufficient condition of integrability of curvilinear integrals containing parameter. And we gained the conditions of exchanging curvilinear integrals containing parameter and triple integral.

curvilinear integrals containing parameter; continuity; integral; property

O186.1

A

1671-6876(2012)03-0241-05

2012-04-26

吴以立(1983-)， 男， 江苏宿迁人， 硕士， 研究方向为组合数学.