基于GIS的上海中心城区大卖场可达性与商圈定量分析

商 硕, 蒋海兵

(盐城师范学院 城市与资源环境学院, 江苏 盐城 224051)

基于GIS的上海中心城区大卖场可达性与商圈定量分析

商 硕, 蒋海兵

(盐城师范学院 城市与资源环境学院, 江苏 盐城 224051)

目前多数基于GIS的商圈模型与技术研究,未全面考虑交通网络、道路等级、网点吸引力与竞争因素.以上海中心城区大卖场为例,借助GIS技术平台,依托可达性方法、Huff模型与商业区位理论等,尝试综合考虑上述因素探讨了大卖场可达性与商圈特征.采用了行进成本分析法测试卖场的可达性与基于可达性的商圈,并在此基础上,根据Huff模型叠加了卖场吸引力因素,得到基于Huff模型商圈.结果表明,上海中心城区整体可达性较高,浦西优于浦东,5～15min卖场可达面积比重最大.

Huff模型; 商圈划分; 可达性; 大卖场

0 引言

我国商业区位研究方法经历由定性与定量研究到定量模拟的过程.20世纪80年代的商业区位研究侧重应用中心地理论对商业中心的规模等级分布进行实证研究[1-3],研究对象多为商业中心,多采用实地调查与聚类分析法,基于中心地理论建立指标体系来划定商业吸引范围.20世纪90年代以来研究方法与技术日趋多样,模型分析、GIS技术与行为分析等方法得以应用,商业中心研究依旧是热点,开始关注商业类型与业态,研究角度从供给与需求两个方面考虑商业中心吸引范围,安成谋采用加权平均模型与希尔伯脱模型研究区位优势度[4],杨吾扬采用“范立农铜心”法预测未来商业中心[5].薛领基于空间相互作用模型,探讨城市内部人口与商业分布及其发展与配置问题,定量地测算各商业吸引范围[6].吴小丁借鉴Huff模型研究对商圈的研究[7].王德等利用上海市交通调查数据从消费者购物出行角度探讨商业中心吸引范围[8].20世纪末,GIS开始作为重要空间分析手段在商业区位研究中得到快速推广.许学强与朱枫运用GIS手段,分别研究广州与上海浦东大型百货商店的空间布局、影响因素及其发展趋势[9-10].进入21世纪,回归模型、选址综合指数、Voronoi图模拟法等数学模型被引入到商业区位分析中.丁鹏飞等基于Relly法则与加权Voronoi图方法,考虑到规模因子划分超市商圈[11].王新生等基于网络Voronoi图方法对大型商业网点市场域进行模拟研究[12].曹嵘等采用回归模型对上海商业布局与交通条件的关系进行实证分析[13].

国外城市地理学领域对服务设施可达性作了较早的研究,1959年Hansen首次提出了可达性的概念,将其定义为交通网络中各节点相互作用的机会大小.国外众多等学者先后对不同类型公共设施的可达性进行了广泛深入探讨[14].近年来国内学者采用GIS技术对城市公共设施可达性进行实证研究,俞孔坚对中山市城市绿地可达性进行定量评价[15],祁毅等基于GIS栅格数据空间可达性建模原理,对吴江市公共设施可达性进行探讨[16].孔云峰使用GIS技术、空间可达性指标和哈夫模型评估学校区域分布[17],张莉等基于GIS技术对仪征医院可达性评价与规划[18],尹海伟采用行进成本法对上海绿地可达性分析[19].

综上所述,基于GIS方法的商业区位与公共设施可达性研究大多采用基于平面欧氏距离的空间分析方法,多数研究缺少交通网络因素而采用基于欧氏距离方法,对于商圈或公共设施服务范围研究,多采用简单的缓冲区方法与服务半径法,少部分研究考虑到交通网络等级因素,但未兼顾设施规模因素,如:行进成本分析法在公共设施可达性方面的研究.部分研究考虑规模因素或道路网络,但未涉及道路等级因素,如:加权Voronoi图与网络Voronoi图方法.本文基于Huff模型与GIS空间分析技术,从城市商业和交通设施供给角度定量地探析卖场空间可达性与商圈.方法兼顾交通网络、道路等级、自然条件与网点规模及竞争因素,较为全面模拟现实商圈影响因素.

大型综合超市、仓储式超市俗称大卖场(以下称卖场),满足一次性购物需求,为食品与日常消费品的主要场所.主要分布在居民居住区、城乡结合部以及交通要道.上海地区近年来开办的如家乐福、麦德龙、易初莲花、易买得、大润发、欧尚等外资大型综合超市、仓储式超市.

1 研究方法

1.1 最近邻距离法

采用最近邻距离法分析卖场空间聚集情况,判断该业态是否可采用行进分析法与Huff模型划分商圈.在空间分析中,点模式分析确定空间对象的空间分布格局,如聚集、随机、规则分布等,点要素空间分布格局探测的常用方法主要是最临近距离分析.通过比较计算观测最近邻的点对的平均距离于随机分布模式中最近邻的点对的平均距离,判断点要素的分布格局是积聚还是扩散分布.

NNI=d(NN)/d(ran)

(1)

式中,NNI为最邻近距离系数,d(NN)为最临近距离,d(ran)为理论的平均距离.

当NNI<1时,样本点呈集聚状态;当NNI>1时,样本点呈分散状态.为了检验计算结果的可靠性,可以采用Z检验.

1.2 行进成本法

行进成本法得到卖场空间可达性与基于可达性的商圈.借助于GIS技术,可达性测度的方法很多,常见方法有缓冲区法、最小邻近距离法、吸引力指数法和行进成本分析法四类.行进成本分析法采用网络距离来表示居住区到网点的最短距离,相对于其它方法与居民实际行进距离较为接近,比其它采用欧氏距离的三种方法优势明显,但未考虑网点吸引力因素.

研究应用GIS软件,通过对相关图形数据与社会经济等属性数据进行整理、录入、转换与配准, 以统一的空间参照系统存储于地理数据库中,其内容包括研究区卖场、水域、道路(分等级)与街道行政数据等. 并以该地理数据库为基础,运用GIS矢量和栅格数据的分析方法,采用行进成本分析法,具体原理见文献[16].

1.3 断裂点公式与Huff模型分析法

断裂点公式基本原理是:总体的客流量与店铺吸引力成正相关,与时间距离或其它阻碍因素成负相关.该法则由空间相互作用的重力模型逐渐演化而来,最初模型为雷利法则,逐渐发展了康帕斯法则、阿普波姆法则、Huff模型与哈夫法则等模型.康帕斯法则(断裂点公式)是对雷利法则的修正,为确定在A和B两城市之间顾客到任何一个区域购物的分界点,位于分界点到A城市的顾客更愿意到A城购物,位于分界点至B城市的顾客更愿意到B城市购物.

断裂点公式:

(2)

(3)

式中:dA为从断裂点到A网点距离;dAB为A和B两网点距离,SA,SB为两地营业面积,Uj为A或者B网点对某地区的吸引力.

Huff模型:

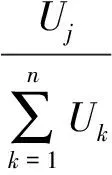
(4)

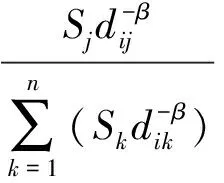
(5)

式中:pij是个体i选择网点j作为目的地的概率,Uj和Uk分别是到j地和k地的可能性,k是供选择的网点序号(k=1,2,…,n).

在测度多个网点商圈时通常采用Huff概率模型理论,将式(3)代入式(4)可得Huff模型式(5),某人到某网点的概率与其网点规模呈正比,并与幂指数的“距离”测度呈反比.式(5)中,S代表营业规模,d代表距离,β>0是摩擦系数,假设β=2.Huff模型的计算结果是概率分布,因此某商圈划分条件是该区域居民到网点j的概率相对于到其它网点具有最大概率分布,网点吸引因素选用网点营业面积,距离采用到某网点最短时间距离.

基本方法:利用行进成本分析法求出每个栅格到所有网点的最短时间,即交通时间成本 (断裂点公式dA部分),再根据Huff模型,比较所有网点相对于某一栅格的引力概率pij,最大者即栅格所归属的网点,最终确定基于Huff模型的网点商圈.

2 方法实现与结果分析

2.1 研究区域与数据来源

研究区域位于上海中心城区(《上海市城市总体规划说明(1999—2010)》),即外环线(A20公路)以内,面积约为667.8 km2.文中将外环线以内的区域称为中心城区.

数据来源包括:上海商业网的2005年中心城区75个大卖场空间与属性数据(营业面积与年代);上海2002年城市道路空间数据(道路等级)与主要水系图;上海中心城区128个街道或镇2000年第五次人口普查资料.

2.2 大卖场集聚特征分析

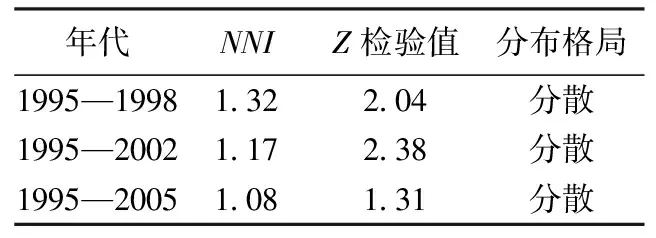
表1 大卖场最近邻域分析

使用ARCGIS中的Average Nearest Neighbor分析工具对上海市中心城区卖场三个时期卖场营业面积做最近邻域分析,得到它们的空间聚集状况参数(表1).可知卖场营业面积在不同时期主要呈现为分散状态,说明该业态为满足消费者便利性购物的需求,商圈具有垄断性[11],卖场要保证足够的商圈才能生存.分散的业态网点间具有很强的竞争性,该业态可采用可达性方法划分商圈.与之相反的是集聚业态,集聚业态注重商圈的共享,满足消费者比较购物行为需要,网点间具有很强的合作性,则不易用该方法对业态商圈进行划分.

2.3 大卖场的可达性定量评价

本文空间可达性是指利用一种特定的交通系统从某一给定区位到达活动地点的便利程度,即所花费的时间成本.用公式表示为Ai=min(Tij),Ai表示可达性,Tij表示从区域某点i到网点j的最短时间,作为Huff模型中的距离变量.商圈是指某商店在地理上吸引范围,影响商圈主要因素包括:市场条件、交通条件和竞争环境.

2.3.1 基于行进成本分析法的可达性分类与商圈划分

行进成本分析法是确定源像元到最近临近像元的最短加权距离,计算单位是成本单位.根据成本加权距离方法计算原理,可达性计算过程为:

1) 成本文件准备(见表2)与源文件准备(卖场空间数据).在成本文件准备中明确居民通过空间某一像元的相对难易程度,选定出行10km所需要的平均时间(以min计)为设定时间成本的参考数值,具体计算公式为:cost(时间成本)=(10/V)×60,式中,V为各类空间对象的设定速度.无道路及街坊小道,采用步行模式,步行平均时速4km/h,有道路采用车行模式,设定快速路为时速40 km/h(外环路),交通主干道的车行速度为30 km/h,次干道车行时速为15 km/h,支路车行道路10 km/h,河流难以通行(桥梁、隧道处外),将黄浦江的成本值设为1 500,吴淞江为1 000,其他河流500[19].按照以上定义设置成本值,采用了10 m分辨率栅格图以达到需要精度,将道路、水系等矢量图层转化成栅格图.学者研究发现,到大卖场购物的消费者出行方式主要为步行、公交车与自行车,乘地铁与轻轨到卖场购物的消费者比重很少[20],故在成本文件准备中忽略地铁轻轨成本.

表2 不同用地类型的相对时间成本值参照

2) 生成可达性时间分类图与基于可达性的商圈图层. 采用叠合方法,生成成本加权距离栅格图层(10m×10m).通过成本加权距离栅格图和卖场图层,利用GIS空间分析模块得到卖场(即任意10 m×10 m栅格到卖场最短时间距离)的可达性栅格图层与服务范围图层.生成卖场可达性栅格图得到累积成本值,累积成本值除以10 000折算成时间,将累积行进成本值转化成实际min数,重新分类将它们分成6个等级,得到可达性时间分类图(图1).

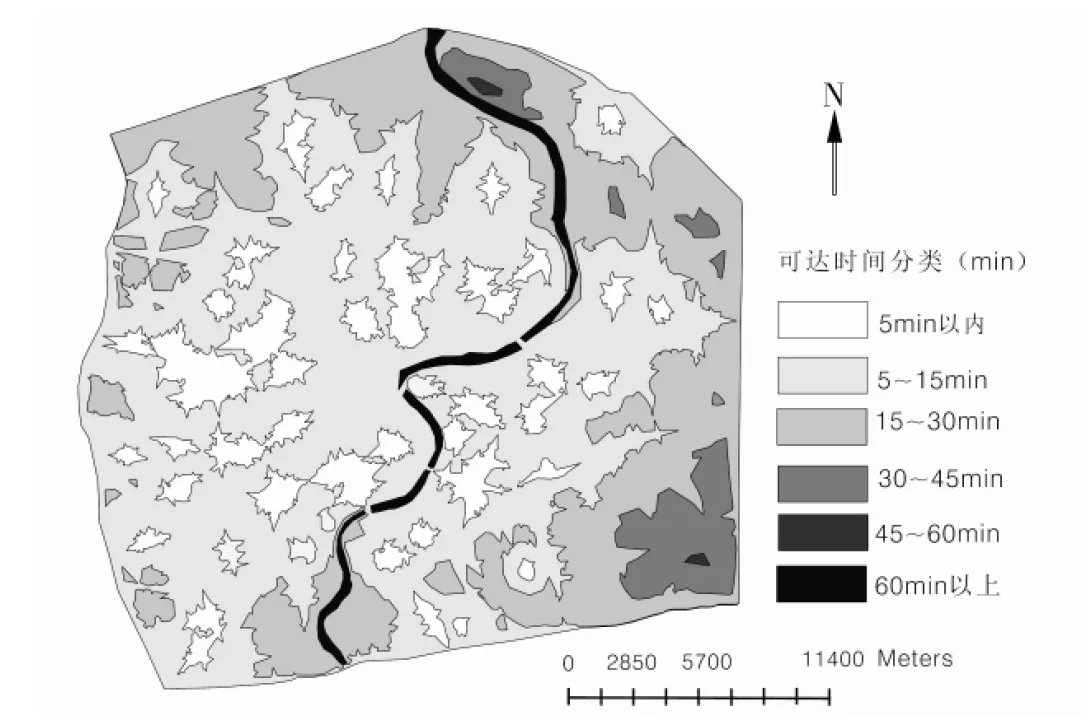
图1 上海中心城区大卖场可达性时间分类图

图2 基于行进成本法的大卖场可达面积分析

2.3.2 大卖场可达性结果评价

计算获得不同时段卖场可达面积数值,得到可达面积分析图表(图2).综合图1与图2可知,5～15min卖场可达面积占比重最大,跨越范围广,15～30min可达面积比重第二,再次是5min可达面积.15min以内可达面积占外环线内总面积65%, 30min内可达面积占外环线内总面积93%,总体上看该区卖场可达情况较好,从图1来看,浦东卖场可达性不及浦西.

表3 上海中心城区待建卖场可进入条件

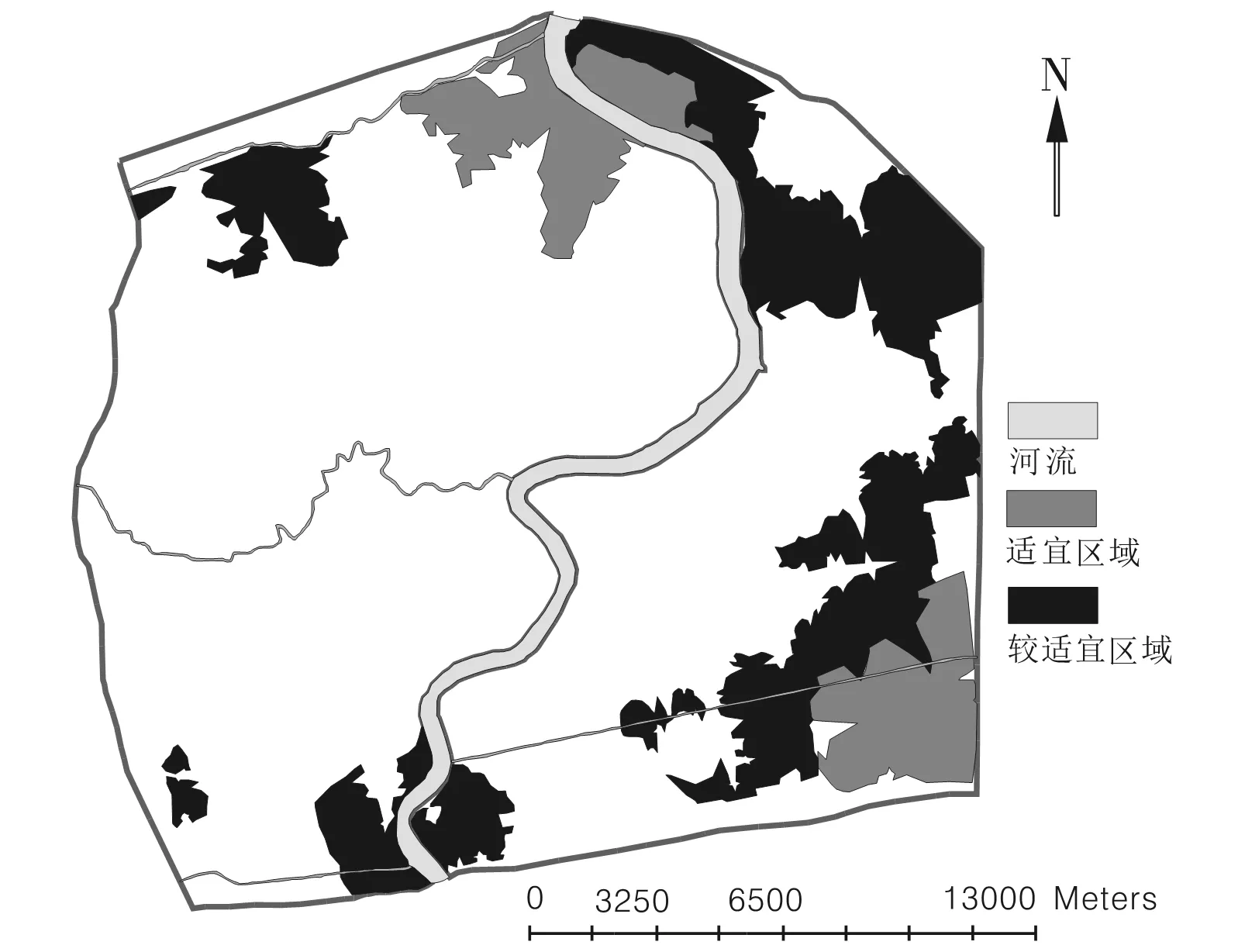
图3 上海中心城区待建卖场可进入区域分析图

将可达时间与区域人口规模作为新建卖场条件(表3),将图1与上海第五次人口普查中居住半年以上人口密度图层叠加,根据表3,得到适宜区域与较适宜区域(图3),该区域为时间可达性差且人口规模大的区域,为网点服务薄弱区域,满足新卖场进入条件,亟需新网点进入.

2.4 基于Huff模型的商圈划分

借助GIS软件平台演绎Huff模型,得到卖场商圈,该商圈模拟考虑到网点自身规模吸引、时间距离与网点竞争因素.商圈生成过程为:首先生成75张不同卖场的时间可达性栅格图层,其次按公式(5)分别结合75张可达性图层与卖场营业面积计算得到75个卖场的可达概率图层,然后对75张概率图层按最大值叠加处理求得所有卖场的基于Huff模型的商圈,最后通过对商圈图层矢量化,运算得到每个卖场商圈面积.

2.5 两种方法下的卖场商圈特征比较

将基于可达性商圈分配图与基于Huff模型卖场商圈图层分别与居住半年以上人口密度图层叠置,得到两种方法下的卖场商圈市场规模图(图4和图5).两图既可说明网点商圈空间格局,也反映商圈市场规模.

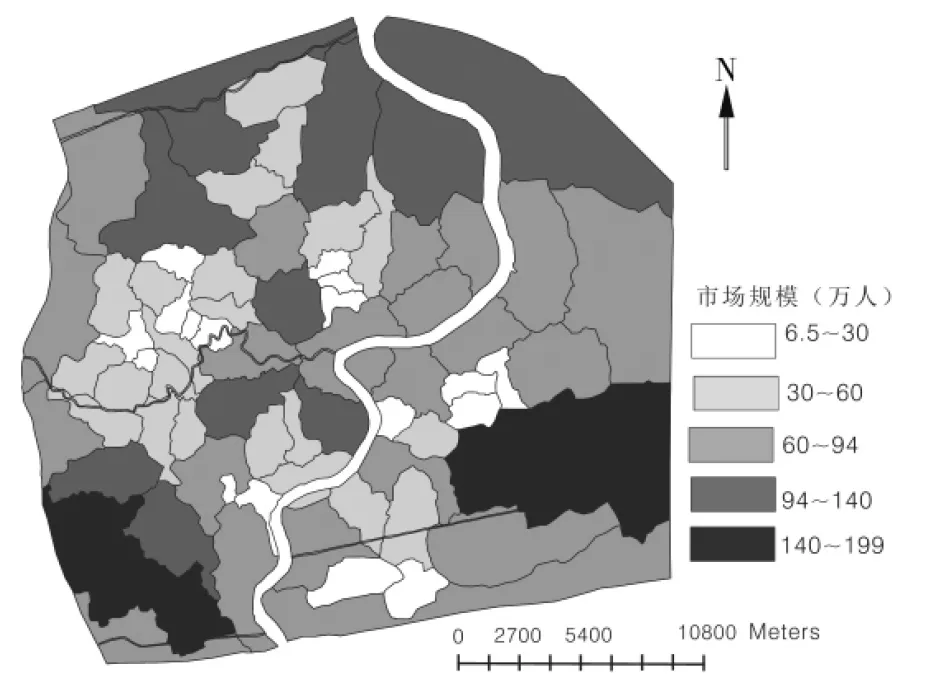
图4 基于可达性的上海中心城区大卖场市场规模分析

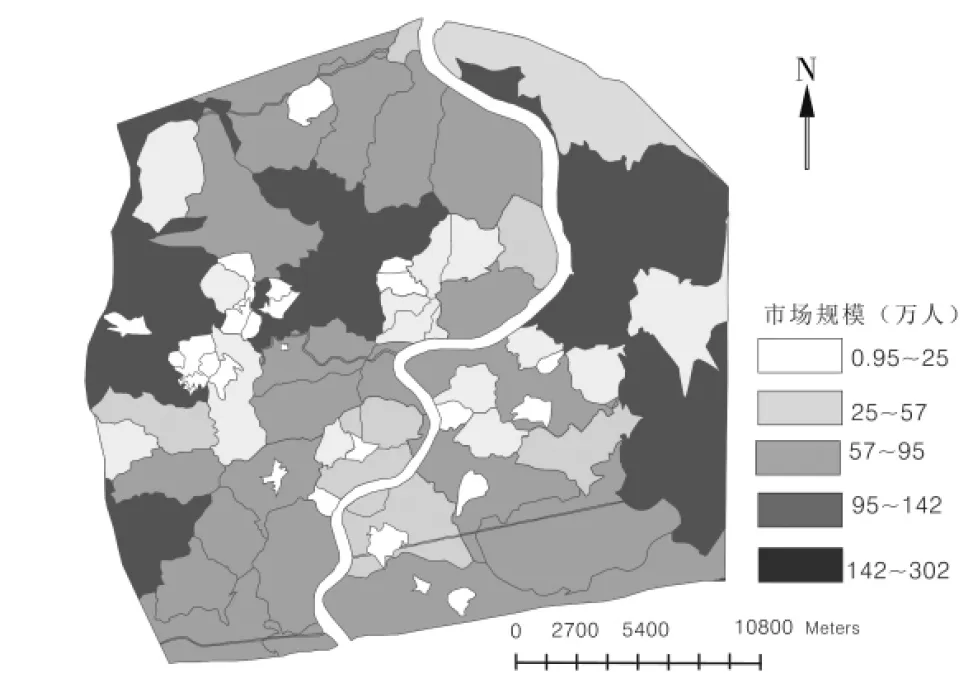
图5 基于Huff模型的上海中心城区大卖场市场规模分析

2.5.1 商圈空间特征比较

从图4来看，基于可达性的商圈划分,考虑到市场竞争与交通因素,单纯反映了商业网点的区位条件.叠加人口密度图层,纳入人口因子,估算市场规模,可进行市场规模分析,为待建网点布局确定提供参考.从总体商圈范围划分来看,商圈面积最大的10个网点分布于外环与中环之间,最小的10个网点位于内环附近,尤其是内中环间西北部与东南部,且分布较密.从市场规模来看,市场规模最大10个网点主要位于外环附近与中心商业区,最小网点分布于内环线外侧附近,特别是城市内中环间西北与东南处网点市场规模小.

从图5来看，基于Huff模型商圈划分,考虑到市场竞争、交通条件与网点规模引力,不仅反映了网点的区位条件,且存在规模因素的贡献,是三种因素组合下的市场范围划分,最接近现实网点的影响范围划分状况.叠加人口密度图层,纳入人口因子,估算市场规模,可进行市场规模分析,为待建网点规模与区位确定提供参考.从商圈面积划分来看,面积较大的网点分布于中外环之间,内环附近的面积较小,特别是西北与东南部,且分布较密.从市场规模来看,市场规模大的网点主要位于中环附近与中心商业区,较低的区域主要分布于内环线外侧附近,特别是内外环间西北部、东南部与北部市场规模较小,网点扎堆明显.

对比图4与图5,不同点在于局部商圈范围与市场规模差异显著.相似点在于网点商圈总体格局基本一致，内环外侧西北、北部与东南商圈面积少、市场规模小,市中心与外围市场规模较大.

2.5.2 商圈统计数据特征比较

利用统计软件得到两种方法下市场规模与商圈面积统计数据(表4).两种方法下的市场规模中位数都小于均值,同为正偏,出现“肥尾”.表明低值数据集中分布,高值数据离散分布.其中基于可达性方法,中位数42.8156万人,小于均值,偏度1.167,数据为正偏度,右边出现“肥尾”特征,峰度为1.14,峰呈“尖顶峰”.基于Huff模型方法,中位数33.8372万人,小于均值,偏度1.538,峰度增为3.355,有较广离散分布“肥尾”特征与更窄的集中分布,“尖顶峰”特征更明显,数据总体上比可达性方法数据更集中,数据集中区域减小,但全距也高于可达性方法,两极分化趋势更为明显.将网点营业面积分别与两种方法下的市场规模作相关分析,结果在显著性水平.α=0.01的双尾检验中,与可达性下的市场规模相关系数为0.038,相关性很弱,与Huff模型下的市场规模相关系数达到0.722,二者显著相关,反映营业规模对市场规模的影响.

表4 基于可达性与Huff模型分析的商圈总体特征统计表

两种方法的商圈面积全距都大,其中基于可达性方法,中位数5.9039km2,小于均值,偏度2.574,数据为正偏度,右边出现“肥尾”特征,峰度为7.802,呈“尖顶峰”,表明大于5.9039平方公里数据相对分散,小于它的数据相对集中.基于Huff模型方法,中位数4.441km2,小于均值,偏度4.09,右边“肥尾”有所增大,峰度增为22.725,“尖顶峰”特征更明显,表明大于4.441km2的较为分散,数据总体比可达性方法更集中,数据集中区域减小,全距也远高于可达性方法.

对比两种方法下统计数据可知:两种方法下商圈面积与市场规模都存在“两极分化”现象.基于Huff模型下两组数据比可达性的偏度和峰度明显增加,数据向低值区域集中,低值区商圈面积与市场规模减小,然而高值区数据分散且数值增大,商圈规模与面积也在增大,表明营业规模因素加强卖场市场规模与商圈面积的“两极分化”,因而在规划网点时,不仅要选对区位,也要考虑网点规模影响.

3 结论与讨论

研究基于可达性方法与Huff模型,运用GIS空间技术与行进成本法定量地分析上海市大卖场可达性,并使其可视化,直观地反映各区域网点供需状况,搜寻到网点可达的薄弱区域.借助GIS技术平台演绎Huff模型模拟商圈特征,探析网点分布问题,扩展了断裂点理论,无疑是新的探索,为新网点选址与布局规划和网点规模确定提供参考.

上海中心城区卖场可达性总体上可达性较好,浦西优于浦东.5～15min卖场可达面积占比重最大,可达性最好的小区分主要布于内环线附近,可达性最差的小区主要分布在外环线附近.两种方法下商圈总体空间格局一致:商圈面积较大区域集中于外环附近,内环附近的面积较小,局部分布较密.市场规模大商圈主要位于外环附近与市中心区.数据统计特征比较,两种方法下都存在低值数据集中分布,高值数据离散分布,商圈市场规模都存在“两极分化”,反映市场竞争激烈地区与网点配置薄弱区并存,基于Huff模型的商圈 “两极分化”特征更为突出.当然商圈特征与空间可达性始终处于动态变化过程中,它会随着城市道路网络、网点增减与人口密度变化而变化.

可达性与商圈模拟,可让规划者了解网点布局情况,为制定合理的网点规划与道路规划提供依据,高效地利用稀缺的区位资源,提高局部地区网点可达性,便于城市居民公平地享受到网点提供的服务.在规划定位网点区位时,也应考虑网点规模定位.经营者既可应用该方法有效地模拟已建网点市场规模与商圈范围,也可对待建网点的商圈与营业规模进行模拟,为商家选址提供参考依据.

由于资料有限,部分数据年代无法统一,假设的人车速度都为匀速等,成本加权距离方法得出的时间距离为最短时间距离,现实中时间距离要比算出的时间距离长.此外本研究从网点供给的角度出发,考虑交通设施的角度分析网点商圈,未过多从购物者需求、购买力与居民购物出行能力角度探讨商圈大小,这些都是未来研究需要改进的地方.

[1] 徐放.北京市商业服务地理[J].经济地理,1984,4(1):40-46.

[2] 宁越敏.上海市区商业中心区位的探讨[J].地理学报1984,39(2):163-172.

[3] 吴郁文,谢彬,骆慈广,等.广州市城区零售商业企业区位布局的探讨[J].地理科学,1988,8(3):208-217.

[4] 安成谋.兰州市商业区位格局与优势度分析[J].地理研究,1990,9(1):28-34.

[5] 杨吾扬.北京零售商业与服务业中心和网点的过去、现在和未来[J].地理学报,1994,49(1):9-17.

[6] 薛领,杨开忠.基于空间相互作用模型的商业布局——以北京市海淀区为例[J].地理研究,2005,24(2):265-273.

[7] 吴小丁.哈夫模型与城市商圈结构分析方法[J].财贸经济,2001(3):71-73.

[8] 王德,张晋庆.上海市消费者出行特征与商业空间结构分析[J].城市规划,2001,25(10):6-14.

[9] 许学强,周素红,林耿.广州市大型零售商店布局分析[J].城市规划,2002,26(7):23-28.

[10] 朱枫,宋小冬.基于GIS的大型百货零售商业设施布局分析——以上海浦东新区为例[J].武汉大学学报,2003,36(3):46-52.

[11] 丁鹏飞,王远飞.基于Relly法则与加权Voronoi图的连锁超市商圈分析[J].上海商学院学报,2005,6(4):12-16.

[12] 王新生,余瑞林,姜友华.基于道路网络的商业网点市场域分析[J].地理研究,2008,27(1):85-92.

[13] 曹嵘,白光润.交通影响下的城市零售商业微区位探析[J].经济地理,2003,23(2):247-250.

[14] 祁毅.基于公共交通可达性的规划支持系统研究[D].南京:南京大学,2008.

[15] 俞孔坚,段铁武,李迪华,等.景观可达性作为衡量城市绿地系统功能指标的评价方法与案例[J].城市规划,1999,23(8):8-11.

[16] 祁毅,徐建刚.基于空间可达性栅格建模的公共设施布局规划分析方法∥创新与发展2006高校GIS论坛论文集[M].北京:中国地理信息系统协会,2006:360-367.

[17] 孔云峰,李小建,张雪峰.农村中小学布局调整之空间可达性分析——以河南省巩义市初级中学为例[J].遥感学报,2008,12(5):800-809.

[18] 张莉,陆玉麒,赵元正.医院可达性评价与规划——以江苏省仪征市为例[J].人文地理,2008,100(2):61-66.

[19] 尹海伟,孔繁花,宗跃光.城市绿地可达性与公平性评价[J].生态学报,2008,28(7):3375-3383.

[21] 柴彦威,沈洁,翁桂兰.上海居民购物行为的时空间特征及其影响因素[J].经济地理,2008,28(2):221-226.

[责任编辑：蒋海龙]

TheQuantitativeAnalysisofBigScaleSupermarketsAccessibilityandTradeAreasDelimitationbasedonGISinCentralShangha

SHANG Shuo, JIANG Hai-bin

(School of Urban and Resource Environment, Yancheng Teachers University, Yancheng Jiangsu 224051, China)

Recently most relative quantitative modeling study on retail location did not simultaneously consider those factors including traffic network,traffic grade,store attraction and competition based on GIS. This paper aims at these shortages and attempt to integrate above factors and make quantitative analysis about large scale shops based on accessibility method,Huff model and GIS technique.This study takes the large scale supermarket of Shanghai central city for example. On one hand,make use of trip cost by GIS analysis to investigate quantitatively supermarket accessibility and visualize the results. On the others,simulate delimitating market area based on trip cost analysis and Huff model which can make

market area more close to actual instance and discuss differences and the same points between market area features of two methods. The result indicates that accessibility of large scale supermarket in Shanghai central city is good,the west of city is better than east. Trade areas between inner loop and middle loop are smaller. Market size near out loop and inside inner loop is greater. Market scale of between inner loop and middle loop is smaller. There is polarization among shops’ market areas and size. The above characteristic shows that the intense competitive market area coexists with the vulnerable competitive region.

accessibility; huff model; large scale supermarket; trade areas delimitation

TP984

A

1671-6876(2012)03-0272-07

2011-10-28

江苏省高校自然科学基金资助项目(10KJD170003)

商硕(1983-), 女, 黑龙江密山市人, 研究方向为城市与区域规划.