基于三角形光强分布光栅投影的三维测量方法

边心田, 徐瑞煜, 程 菊

(淮阴师范学院 物理与电子电气工程学院, 江苏 淮安 223300)

基于三角形光强分布光栅投影的三维测量方法

边心田, 徐瑞煜, 程 菊

(淮阴师范学院 物理与电子电气工程学院, 江苏 淮安 223300)

针对相位测量轮廓术中正弦光栅制作工艺复杂的问题,提出一种基于三角形光强分布光栅投影测量物体三维形貌的方法．测量时,将三角形光强分布光栅投影到被测物体表面,摄像机获取变形条纹图,通过系统参数和条纹图携带的相位信息求解出物体的三维面形．推导出通过三角形光强分布光栅求解相位的公式．实验结果表明,提出的方法具有较高的精度和可行性．

三维测量; 三角形光栅; 相位测量轮廓术

0 引言

基于结构光投影的三维形貌测量技术具有非接触、快速、精度高、自动化程度高等优点成为三维测量领域的研究热点[1-4],在工业检测、质量控制、生物医学、实物仿形等领域得到大量深入研究并且被广泛应用．

在投影测量中,相位测量轮廓术具有对背景、对比度和噪声变化不敏感,精度高,易于实现自动化测量等优点,一直是研究的重点之一[5,6]．传统的相位测量轮廓术主要是采用正弦光栅投影,进行三维面形测量,这种方式的优点是测量精度高,但是其应用受到正弦光栅制作工艺的限制,标准的正弦光栅制作难度很大,在实际应用中难以批量生产,不仅提高了相关仪器的成本,也限制了相位测量轮廓技术的发展．由于三角形光强分布光栅[7,8]透过率函数是线性的,容易控制,降低了制作的难度,只需在玻璃平板上开一小槽,然后添入均匀地吸收介质就可制成．所以从制作工艺,生产成本,普及相位测量轮廓术等角度来讲,研究使用三角形光强分布光栅具有重要的现实意义．本文基于相位测量轮廓术的原理,提出利用三角形光强分布光栅进行投影的三维形貌测量技术,推导出基于三角形光强分布光栅的相位求解公式,实验表明提出方法具有较高的精度和可行性．

1 测量原理

相位测量轮廓术一般是采用正弦光栅投影和数字相移技术,以高精度和较快速度获取并处理大量的三维数据．当以三角形光栅代替相位测量轮廓术中的正弦光栅时,构造函数sow()和cow()对应于正弦光栅中的函数sin()和cos(),因此sin()和cos()的图形可作如图1和图2所示的代换．

由图1可知,sowx的函数解析式为:

(1)

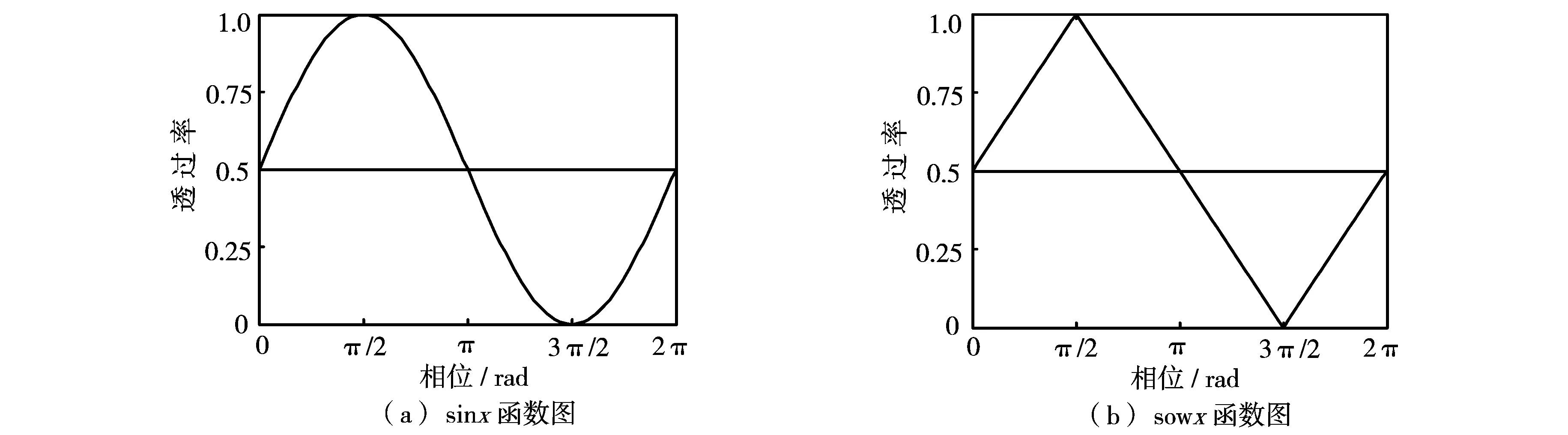
图1 sinx函数和sowx函数图

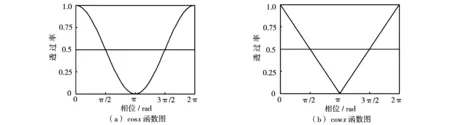
图2 cos()函数和cow()函数图

由图2可知,cow()的函数解析式为:

(2)

将一个三角形光强分布光栅投射到一个漫反射物体上,其变形条纹图像可表示为:

I(x,y)=A(x,y)+B(x,y)cowφ(x,y)

(3)

其中A(x,y)为背景强度,B(x,y)/A(x,y)为条纹对比度,结合(2)式,令

第一帧:

I1(x,y)=A(x,y)+B(x,y)cowφ(x,y)

第二帧:

A(x,y)-B(x,y)sowφ(x,y)

(4)

第三帧:

A(x,y)-B(x,y)cowφ(x,y)

(5)

第四帧:

A(x,y)+B(x,y)sowφ(x,y)

(6)

因此

I4(x,y)-I2(x,y)=2A(x,y)sowφ(x,y)

(7)

I1(x,y)-I3(x,y)=2A(x,y)cowφ(x,y)

(8)

与函数tan()对应的towφ(x,y)=sowφ(x,y)/cowφ(x,y),其反函数用atow()表示,由(7)(8)可得:

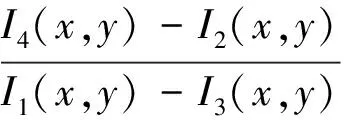
(9)

因此可得相位:

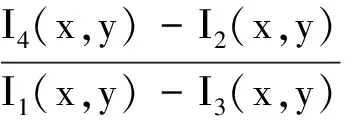
(10)

由(10)式计算出的相位函数φ(x,y),被截断在反函数atow()的主值(-π,π)范围内,是不连续的,必须将其展开成原有的连续相位分布φu(x,y)．然后再根据相位(高度映射公式)计算出被测物体的形貌．一般情况下,采用远心光路系统,在基准平面上的相位分布是线性的．根据几何知识可知,物体的三维面形信息可用高度分布表示[1]为

(11)

式中,d和L是系统结构参数,AC是与相位分布φu(x,y)有关的函数．根据(11)式中高度与相位之间的映射关系就可以求出被测物体的形貌．

2 实验

为了验证基于三角形光强分布光栅的相位测量轮廓术对恢复高度的准确性,我们进行计算机仿真实验,借用MATLAB软件生成一个高度为3cm的物体,物体形状如图3所示,其函数表达式表示为:

z(x,y)= 3{3(1-x)2exp[-x2-(y+1)2] -

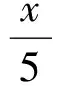
(12)

为了评估该方法的抗干扰和抗噪声的能力,在模拟实验中加入5%的随机噪声．将三角形光强分布光栅投射到漫反射物体上,从另一方向观察投射条纹,由于物体的表面凹凸不平,所以摄像机获得受高度调制的变形条纹图像,如图4所示．这些变形的条纹图包含了物体的高度信息．利用四步相移法解调出的模拟物体的相位分布,然后根据相位(高度映射公式)恢复物体的面形分布如图5所示．恢复物体的面形与模拟物体面形的差值如图6所示．由图6可以看出,实验中添加5%的随机噪声后,测量误差仍能保持在0.04cm以内,本方法具有较好的抗噪性能．

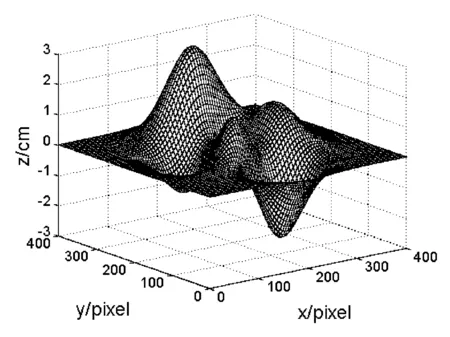
图3 模拟生成的待测物体图

图4 变形的三角形光栅图

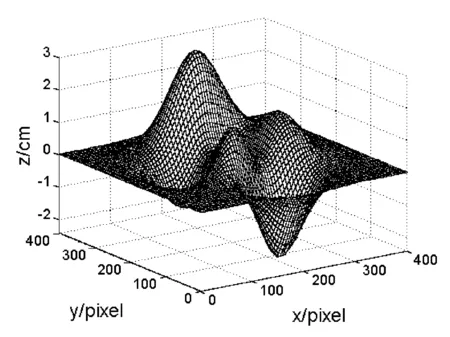
图5 恢复得到的物体面形

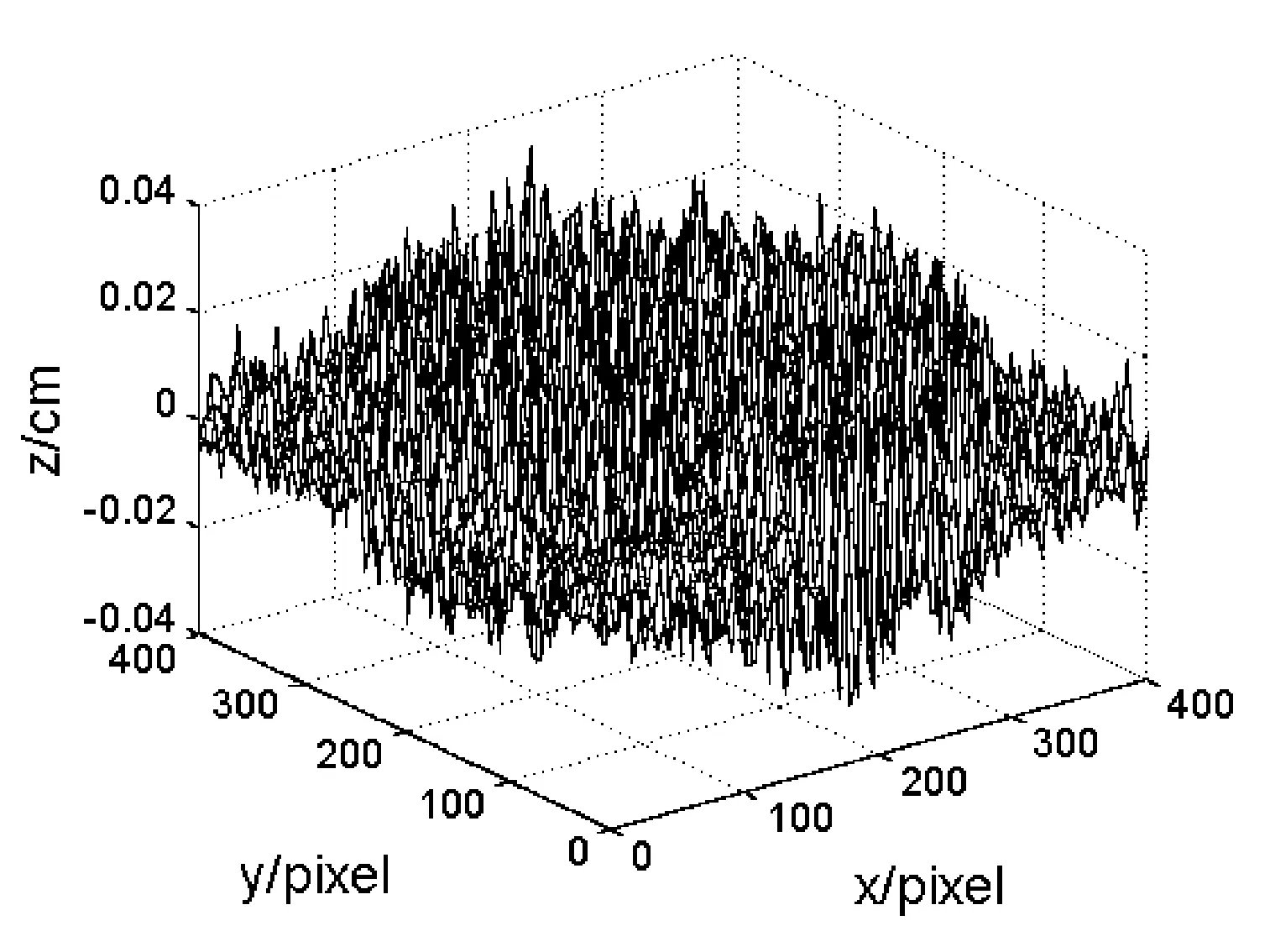
图6 加入5%噪声后的误差图

3 结论

本文提出了基于三角形光强分布光栅投影测量物体三维形貌的方法.通过对三角形光强分布光栅投影到被测物体表面产生的变形条纹进行分析计算,恢复出物体的三维形貌．推导出相位计算公式并对测量方法进行了实验验证．三角形光强分布光栅制作工艺简单,应用于投影测量精度较高．因此,基于三角形光强分布光栅的相位测量轮廓术具有较强的可行性与推广价值,有利于促进相位测量轮廓术的普及应用．

[1] 苏显渝. 信息光学[M]. 北京:科学出版社,2011.

[2] 王露阳,达飞鹏. 基于互补色编码条纹投影的三维形貌测量方法[J]. 光学学报,2011, 31(6): 0612004.

[3] Cho Jui Tay, Madhuri Thakur and Chenggen Quan. Grating projection system for surface contour measurement[J]. Appl Op, 2005, 44(8):1393-1400.

[4] Bian X T, Su X Y, Chen W J. Analysis on 3D object measurement based on fringe projection[J]. OPTIK, 2011, 122:471-474.

[5] Zhang S, Daniel V D, Oliver J. Superfast phase-shifting method for 3-D shape measurement[J]. Optics express, 2010, 18(9):9684-9689.

[6] 朱林,达飞鹏,盖绍彦. 相位测量轮廓术中一种有效补偿相移误差的新算法[J]. 东南大学学报:自然科学版,2010,40增刊(1):302-307.

[7] Jia P R, Kofman J. Multiple-step triangular-pattern phase shifting and the influence of number of steps and pitch on measurement accuracy[J]. Appl Opt, 2007, 46(16): 3253-3262

[8] 叶虹呐,曹益平. 基于三角形分布光栅的相位测量轮廓术[J]. 中国激光,2011, 38(11): 1108001.

[责任编辑：蒋海龙]

3DShapeMeasurementTechniquebasedonTriangularPatternGratingProjection

BIAN Xin-tian, XU Rui-yu, CHENG Ju

(School of Physics and Electronic Electrical Engineering, Huaiyin Normal University, Huaian Jiangsu 223300, China)

According to the complicated manufacturing technique of sinusoidal grating in Phase measuring profilometry (PMP), the paper presents a new method to measure the 3D shape based on the triangular-pattern grating. When measuring, the triangular-pattern grating was projected to the surface of the object, and the camera captures the stripes image. The 3D shape of the object may be reconstructed by the phase information that the fringe pattern carries. Some calculation formulas for phase and height are derived. The experimental results show that the method is reliable, and can carry out 3D shape measuring with high precision.

3D measurement; triangular-pattern grating; phase measuring profilometry

O438.2

A

1671-6876(2012)04-0354-04

2012-09-01

淮安市科技支撑计划项目(HAG2012044)

边心田(1978-), 男, 山东淄博人, 讲师, 博士, 主要从事光学三维传感和视觉测量方面的研究.