2011年全国高中数学联赛一试压轴题的源流

●

(乐清中学 浙江乐清 325600)

2011年全国高中数学联赛一试压轴题的源流

●钱从新

(乐清中学 浙江乐清 325600)

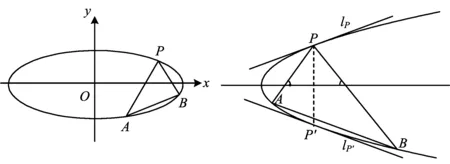
图1 图2

(1)证明：△PAB的内切圆的圆心在一条定直线上；

(2)若∠APB=60°，求△PAB的面积．

本题根源在于椭圆的一个性质：对于标准方程的椭圆，当椭圆上过点P的切线的斜率与弦AB所在的直线的斜率为相反数时，直线PA与PB的斜率也必为相反数，从而内切圆圆心在过点P垂直于一条坐标轴的直线上．此性质非椭圆独有，而是圆锥曲线的通性，其逆命题也成立．下面试为其进行拓广证明．

性质1设P与P′是圆锥曲线上关于其一条对称轴对称的任意一对对称点，过点P,P′作该曲线的2条切线分别为lP与lP′，如果该曲线的弦AB所在的直线lAB与lP′平行，则直线PA,PB与该对称轴所成的夹角相等(如图2)．

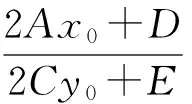
(A+Ck2)x2+(2Ckb+D+Ek)x+(Cb2+Eb+F)=0，

可知

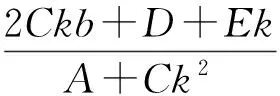
(1)

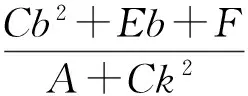
(2)

欲证直线PA，PB与该对称轴所成的夹角相等,即证kPA+kPB=0,即

(y1-y0)(x2-x0)+(y2-y0)(x1-x0)=0.

将y1=kx1+b,y2=kx2+b代入上式，整理得

将式(1)，式(2)代入式(3)，整理化简得

(2Cx0y0+Ex0)k2+(Eb+2F+2Cby0+Ey0+Dx0)k+(y0-b)(2Ax0+D)=0,

当lP斜率不存在时，P与P′应是曲线水平方向对称轴上的2个顶点，由图形的对称性可直接得知直线PA,PB与该对称轴所成的夹角相等．

由于方程Ax2+Cy2+Dx+Ey+F=0包含了圆的情形，因此性质1对于圆也成立．

性质2设P与P′是圆锥曲线上关于其一条对称轴对称的任意一对对称点，如果过点P的2条弦PA,PB所在的直线与该对称轴所成的夹角相等，那么弦AB所在的直线lAB与过P′的切线lP′平行．

证明同上所设．由直线PA，PB与该对称轴所成的夹角相等得

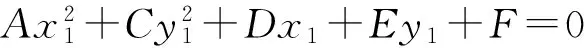
由式(4)，式(5)可得

同理可得 (x1-x0)[A(x2+x0)+D]=(y1-y0)[C(y2+y0)+E],

(7)

式(6)-式(7)，化简得

(x2-x1)(2Ax0+D)=(y2-y1)(2Cy0+E).

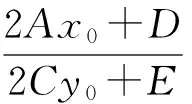
性质2对于圆同样成立．利用性质1，可以得到原题的如下拓广．

图3

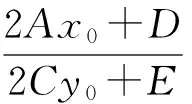
又设∠APB=α，则当∠APB的平分线垂直于x轴时，

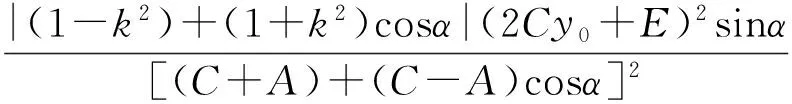
当∠APB的平分线垂直于y轴时，

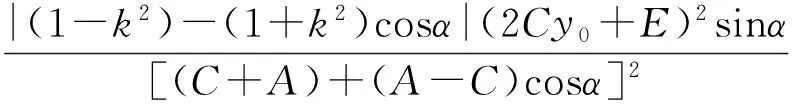
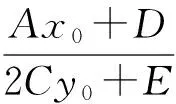
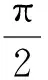
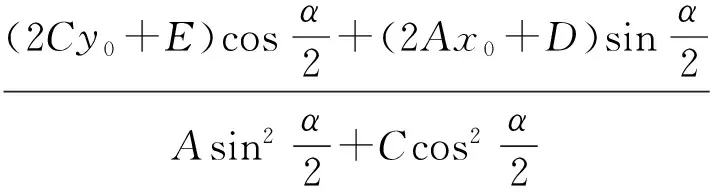
同理可得

从而

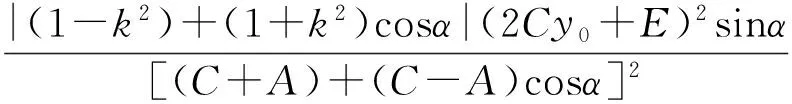
当∠APB的平分线垂直于y轴时，则以∠APB的补角π-α替换上式中的α，即得