让数学竞赛走近更多师生——2012年浙江省高中数学竞赛试题评析
2012-11-07
●
(杭州学军中学 浙江杭州 310012)
让数学竞赛走近更多师生——2012年浙江省高中数学竞赛试题评析
●郑日锋
(杭州学军中学 浙江杭州 310012)
长期以来,许多师生觉得数学竞赛试题深不可测,认为只有竞赛教练或参加竞赛辅导的学生才可以去研究或做数学竞赛试题,因此避而远之.其实,近几年来,从全国高中数学联赛一试到大部分省市的数学竞赛试题都在降低难度上下了功夫,旨在让更多的高中学生参与到数学竞赛活动中来,让学生感受到数学的魅力,培养学习数学的兴趣.因此许多数学竞赛试题实际上是教材知识的拓展与深化,呈现出“高考化”的倾向,有人认为省数学竞赛试题是提前了2个月的高考.2012年浙江省高中数学竞赛试题继承了前3年试题的特色,在平凡中见新奇,刻意降低了试题难度,真正体现了让数学竞赛走近更多师生.本文简述其特点.
1 高考味
1.1 降低试题的起点
试卷第1,2,3,4,5,6,7,11题,考查高中数学的基础知识,这些题目来源于课本,解决的方法都是基本方法,难度与高考试题中的基础题相当,这种降低试题起点的做法能增强学生解题的信心.
1.2 突出数学思想方法的考查
试卷对函数与方程思想、分类讨论思想、数形结合思想、转化思想等进行了全面的考查.
第10题设f(x)=x2+bx+c,若方程f(x)=x无实根,则方程f(f(x))=x
( )
A.有4个相异实根 B.有2个相异实根
C.有1个实根 D.无实根
分析本题是一个迭代函数的不动点问题.已知f(x)没有不动点,判断二阶迭代函数有几个不动点.因为y=f(x)-x是二次项系数为正数的二次函数,所以f(x)>x对任意x∈R恒成立(否则若存在x1∈R使f(x1)
第14题已知实数a,b,c,d满足ab=c2+d2=1,则(a-c)2+(b-d)2的最小值为________.
分析本题若从代数的角度很难找到解题思路,但从几何角度便能轻松解决.
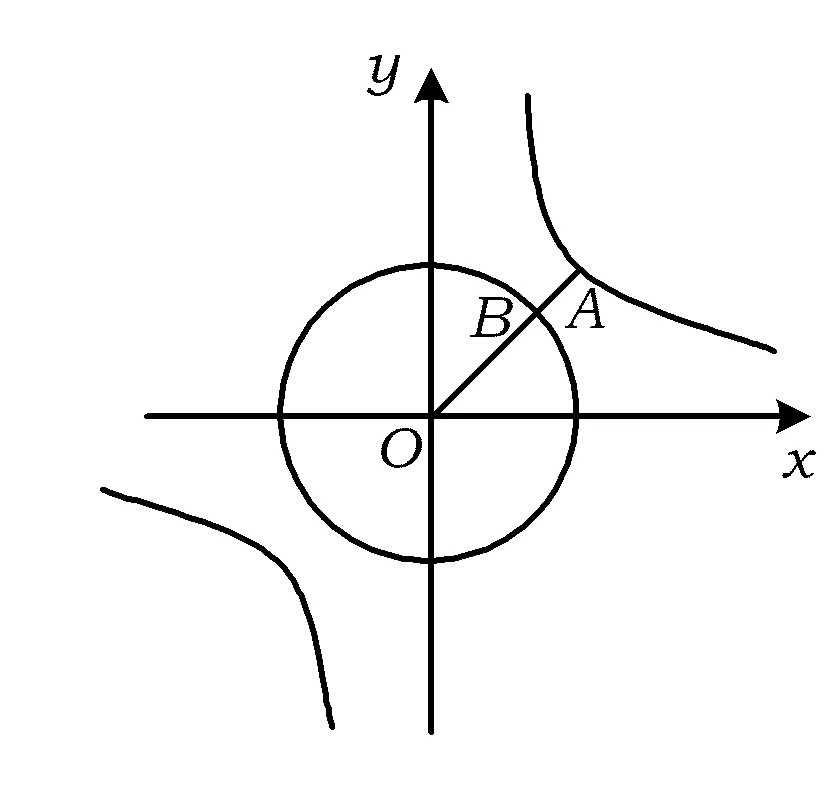
图1


分析本题要解含有绝对值的三角方程,通常的思路是去掉绝对值,分2种情况讨论:
(1)若cosx≥0,则
1-cosx=sinx(1+cosx),
即
sinxcosx+sinx+cosx-1=0.
设sinx+cosx=t,则
t2+2t-3=0,
解得
t=1(t=-3舍去),
因此
sinx+cosx=1,
即
sinx=1,cosx=0或sinx=0,cosx=1.
(2)若cosx<0,同理可得
sinx=0,cosx=-1.

本题体现了分类讨论思想.



显然,N∈Z+,且x1,x2是方程x2-2Nx+qn=0的2个根.由x1≤x2,得

本题体现了转化思想.
2 竞赛味
2个附加题,第21题属于平面几何问题,第(1)小题比较简单,只需利用弦切角与夹弧所对的圆心角的关系;第(2)小题,需利用对边之和相等的四边形是圆外切四边形;第(3)小题只需证2个圆的圆心重合,这需要利用圆外一点作圆的切线的性质.平面几何历来是数学竞赛的热点内容,本题难度并不大.第22题属于离散函数的值域问题,需要利用2个整数的和与差具有相同的奇偶性,并通过构造证明各函数值的存在,这个题目的答案可以猜出来.本题是全卷中较难的,并具有较浓竞赛味的一个问题.
3 研究味
一份好的试卷往往能让人回味无穷,作为一线教师需要对试题进行多方位的探索.
3.1 优解

分析除命题者提供的解答外,以下的解答更简便.
设P(m,0)(-5≤m≤5),A(x1,y1),B(x2,y2),则直线AB的方程为x=m+ty.由
得
(16t2+25)y2+32mty+16m2-400=0,

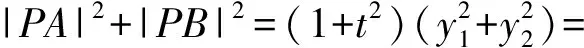
(1+t2)[(y1+y2)2-2y1y2]=


3.2 延伸
第10题可以进行如下拓展:
拓展1设f(x)是定义域为I的连续函数,且f(x)∈I,f1(x)=f(x),fn(x)=f(fn-1(x))(n≥2,n∈N*),则由函数y=f1(x)-x不存在零点,可得对任意n∈N*,函数y=fn(x)-x都不存在零点.
有兴趣的读者可查看文献[1].

此题可以进行如下拓展:

证明过程与原题相仿.
第22题设i1,i2,…,i10为1,2,…,10的一个排列,记S=|i1-i2|+|i3-i4|+…+|i9-i10|,求S可以取到的所有值.
经过探究,本题可以进行如下拓展:
拓展3设n为正偶数,i1,i2,…,in为1,2,…,n的一个排列,记S=|i1-i2|+|i3-i4|+…+|in-1-in|,则
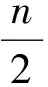
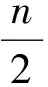
3.3 认识
第21题第(2)小题,标准答案中直接利用对边之和相等的四边形是圆外切四边形,不证明直接应用,而平面几何书籍中只指出,圆外切四边形的对边之和相等,没有研究其逆命题是否成立,因此应先证明逆命题成立.
第13题作为B卷的试题考查了反正弦函数,超出了新课程标准要求的范围,非附加题的试题考查的内容应局限在高考范围内比较合适.
[1] 郑日锋.一类迭代函数零点问题解决的心路历程[J].中学数学教学参考,2011(8):63-64.
