立足双基 关注热点 把握范围——谈三角函数的自主招生备考
2012-11-07
●
(绍兴市第一中学 浙江绍兴 312000)
立足双基关注热点把握范围——谈三角函数的自主招生备考
●虞金龙
(绍兴市第一中学 浙江绍兴 312000)
三角函数是一种重要的函数,它的定义和性质独特,在自主招生中是对基础知识和基本技能考查的重要内容之一.因此在备考时,要在三角函数的灵、活、巧上下功夫,在备考前,应立足双基,关注热点,把握范围.
1 立足双基
三角函数是基本初等函数之一,要充分关注三角公式的灵活运用,巧妙利用特殊角进行角的变换,合理利用三角函数的图像和性质进行解题.
1.1 灵活运用公式

( )
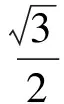
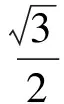
(2011年清华大学等七校联考试题)
解由降幂公式得




评注公式多是三角函数的一大特点,如何灵活运用公式是夯实三角函数双基的基本途径.本题主要考查三角函数的和差公式、降幂公式及三角恒等变形公式.本题的解题关键是利用条件将所给的函数“化一”,即变形为一个角或一个三角函数的形式.一般来说,求解三角函数的周期、最值等问题,都可以利用“化一”的方法,因此考生要给予重视并熟练运用.
1.2 巧化角的变换
例2求sin410°+sin450°+sin470°的值.
(2010年清华大学自主招生试题)
解sin410°+sin450°+sin470°=
cos480°+cos440°+cos420°=

2cos40°+cos2160°+cos280°+cos240°)=

评注角的变换是三角函数考查的重点之一,由于题目的形式各不相同,因此解题方法也因题而异.从整体上讲,角的变换要着重抓住“特殊角”,考虑角与角之间的关系.本题主要利用三角公式,巧妙利用角的变换达到解题目的.
1.3 合理利用性质
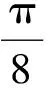
(1)求φ的大小;
(2)当x∈[0,π]时,方程f(x)-m=0恰有2个不同的实根,观察f(x)的图像,写出m的取值范围.
(2009年华中科技大学自主招生试题)
解(1)函数f(x)=-[sin2(x+φ)+
cos2(x+φ)]=
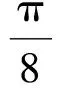
又因为

所以
φ=0.
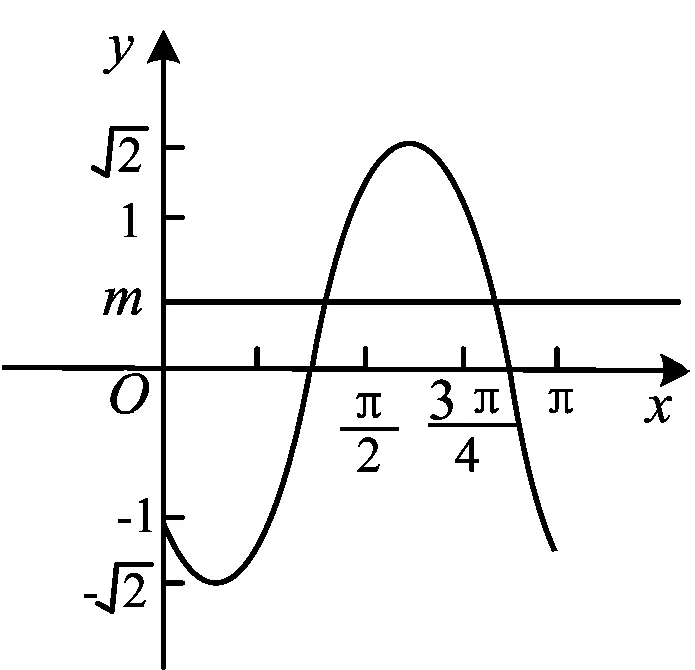
图1
(2)由第(1)小题知
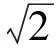
评注三角函数的图像和性质是三角函数的核心问题,自主招生试题中也常对性质进行考查,主要利用数形结合的思想,有时灵活性较大并有一定的难度.
2 关注热点
在历年的自主招生试题中,三角形中的问题是考查的热点之一,此类问题主要利用正弦、余弦定理和内角和定理,在复习时要注意把握热点,做到有的放矢.
2.1 关注三角形中的问题
例4已知△ABC不是直角三角形.
(1)证明:tanA+tanB+tanC=tanAtanBtanC;
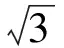
(2011年清华大学等七校联考试题)
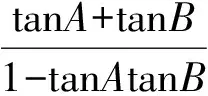
tanA+tanB=tan(A+B)(1-tanAtanB).
因为△ABC不是直角三角形且A+B+C=π,所以A+B=π-C,从而
tanA+tanB= tan(π-C)(1-tanAtanB)=
-tanC+tanAtanBtanC,
因此
tanA+tanB+tanC=tanAtanBtanC.
(2)依题意,知
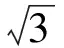
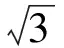
由第(1)小题,得

从而

又根据题意有

从而

即
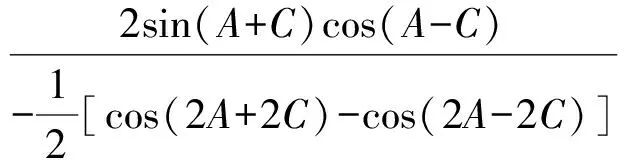

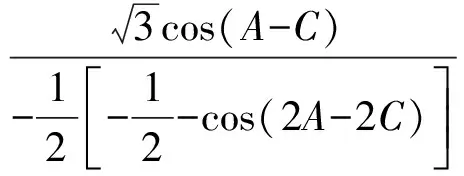
整理得
3cos(A-C)= 1+2cos(2A-2C)=
4cos2(A-C)-1,
即
4cos2(A-C)-3cos(A-C)-1=0,
解得

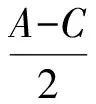
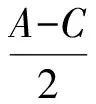
评注三角形中的问题是历年自主招生的热点之一,本题主要利用三角形的内角和定理及和角公式.
2.2 重视正、余弦定理的应用

( )
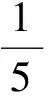
(2010年清华大学等五校联考试题)


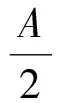
解法2由正弦定理可将a+c=3b变形为
sinA+sinC=3sinB=3sin(A+C),
右边展开并整理可得
sinA(1-3cosC)+sinC(1-3cosA)=0,
即
从而
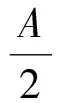
即
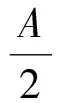
评注在历年的自主招生试题中,利用正余弦定理设计考题是考查重点之一.本题主要利用正弦定理、内角和定理及角的和差公式.
3 把握范围
由于各地高考要求不一,因此考生必须了解自主招生命题的范围.纵观近几年各校的自主招生试题,对三角公式的要求比较高,除记住二倍角公式外,对三倍角公式也有一定的要求.另外,积化和差、和差化积公式也屡有见到,考生在复习时必须把握好.北京大学等名校还时常考查三角函数与其他内容的综合问题,考生必须针对自己的招生学校把握好复习范围.
3.1 熟记特殊公式
例6三角形的3条边长为连续整数.
(1)是否存在这样的三角形,其最大角是最小角的2倍?
(2)是否存在这样的三角形,其最大角是最小角的3倍?
(2005年上海交通大学保送、推优生数学试题)
解设三角形的最大角为α,最小角为β,3条边长为n,n+1,n+2.
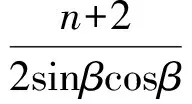
从而
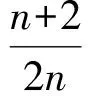
又因为
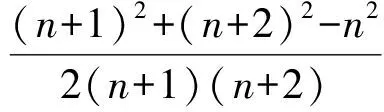

所以
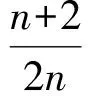
解得n=4,故所求三角形的3条边长为4,5,6.
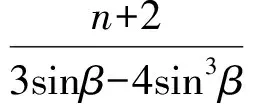
从而

因为

所以
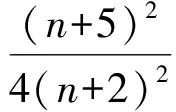
即
n3-9n+8=0,
亦即
(n-1)(n2+n-8)=0,
解得

当n=1时,3条边长1,2,3不能构成三角形,因此不存在这样的三角形.
评注本题考查二倍角、三倍角公式,主要利用正、余弦定理,此题还有其他解法,但笔者认为此解法属较简单的解法之一.
3.2 重视综合运用
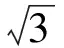
(2009年北京大学自主招生试题)
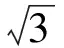

即


评注此题是三角与数论的简单组合,此题解法较多,此解法简洁易懂,但考生对分类讨论思想的运用有一定的困难,因此不易想到此解法.
目前,各校自主招生要求不同,现在又出现“北约”、“华约”、“卓越”、复旦大学“千分考”等.由于自主招生没有确切的考纲,针对三角函数这块知识的考查,往往高于高考要求,因此笔者认为考生在应考时要关注到这一特点,只有针对自己报考学校的要求而采取相应的复习方式,才能在自主招生考试中稳操胜券.
