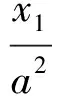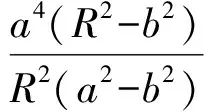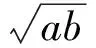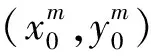解析几何竞赛题的解题方法
2012-11-07
●
(杭州高级中学 浙江杭州 310003 )
解析几何竞赛题的解题方法
●周顺钿
(杭州高级中学 浙江杭州 310003 )
解析几何的本质是用代数方法研究几何问题,其核心思想是数形结合.解决解析几何问题的根本方法是坐标法:建立恰当的坐标系,设点的坐标,设曲线的方程,列出关系式,再进一步找联系、找转化点,实现问题的解答,最后加以验证.把这样的解题思维链优化为“建、设、列、解、验”五字诀,其中“设、列、解”是常用的解题方法.
通过坐标方法将几何问题转化为代数问题,其解题过程中的关键是减少运算量.
有关直线与圆的问题,利用圆和直线的几何性质就可降低运算量;有关圆锥曲线的问题,采用圆锥曲线的定义、设而不求的方法和一元二次方程的韦达定理是解题的通性通法;选择曲线的参数方程、极坐标方程也能简化解题过程.
1 利用平面几何性质
例1已知直线L:x+y-9=0和圆M:2x2+2y2-8x-8y-1=0,点A在直线L上,B,C为圆M上的2个点.在△ABC中,∠BAC=45°,AB过圆心M,则点A横坐标的取值范围为______.
(2009年全国高中数学联赛试题)

(2006年全国高中数学联赛试题)

又由圆幂定理得
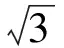

代入式(1),式(2)得
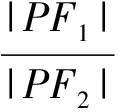

评注灵活运用平面几何性质,是减少解几运算量的有效途径.
2 利用圆锥曲线的定义

( )
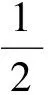
解设PI延长线交x轴于点Q,则

于是

故选A.
例4设双曲线x2-y2=1的左、右焦点分别为F1,F2,若△PF1F2的顶点P在第一象限的双曲线上移动, 求△PF1F2的内切圆的圆心轨迹以及该内切圆在边PF2上的切点轨迹.
(2005年浙江省高中数学竞赛试题)

图1
解如图1,记双曲线在x轴上的2个顶点为A(1, 0),B(-1, 0),G为△PF1F2的内切圆在边F1F2上的切点,H为△PF1F2的内切圆在边PF2上的切点,K为△PF1F2的内切圆在边PF1上的切点,则
|GF1|-|GF2|=|KF1|-|HF2|=
(|KF1|+|KP|)-(|HF2|+|HP|)=
|PF1|-|PF2|.
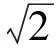
因为P(x,y)是在x2-y2=1第一象限的曲线上移动,当PF2沿双曲线趋于无穷时,与x轴正向交角θ的正切的极限是
从而
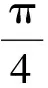
故点H的轨迹方程为
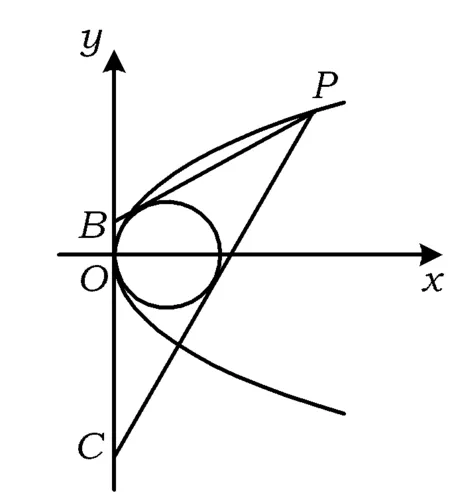
也可以用直角坐标形式.由于点G与A(1, 0)重合,是定点,故该内切圆圆心的轨迹是直线段,方程为x=1(0 评注充分利用圆锥曲线的定义,抓住本质. 例5如图2,P是抛物线y2=2x上的动点,点B,C在y轴上,圆(x-1)2+y2=1内切于△PBC,求△PBC面积的最小值. (2008年全国高中数学联赛试题) 图2 解设P(x0,y0),B(0,b),C(0,c),不妨设b>c,则直线PB的方程 整理得 (y0-b)x-x0y+x0b=0. 又圆心(1,0)到PB的距离为1,从而 易知x0>0,上式化简得 (x0-2)b2+2y0b-x0=0, 同理有 (x0-2)c2+2y0c-x0=0, 从而 于是 评注本题视b,c为方程的2个根,利用韦达定理减少了运算量. (1)求a,b之值; (2)设点A坐标为(6, 0),B为椭圆C上的动点,以A为直角顶点,作等腰直角△ABP(其中A,B,P按顺时针方向排列),求点P的轨迹方程. (2008年浙江省高中数学竞赛试题) 解(1)设c为椭圆的焦半径,则 于是 a=5,b=3. (2)设B(x1,y1),,P(x,y),|AB|=r,则以A为圆心,r为半径的圆的参数方程为 设AB与x轴正方向夹角为θ,点B的参数表示为 点P的参数表示为 即 又由于点B在椭圆上,可得 此即为点P的轨迹方程. 解设A(x1,y1),B(x2,y2),则过点A的椭圆E的切线方程为lA: 过点B的动圆C的切线方程为lB: x2x+y2y=R2. 因为直线lA,lB重合,所以 代入椭圆方程,得 又OB⊥AB,有 OA2=AB2+R2, a2+b2-2ab, (2006年全国高中数学联赛试题) 证明因为y2=nx-1与y=x的交点为 显然有 nkm-km-1(m≥2) . (8) 由于k1=n是整数,得 解析几何综合题是全国高中数学联赛一试的必考题.从上述例题可以看出,解析几何题难度大、要求高、思维活,但只要我们遵循考纲、夯实基础、拓宽思路、沟通知识间的纵横联系,熟练掌握数形结合、化归转化等思想方法,必能适应数学竞赛的要求,解答好解析几何竞赛题.3 利用韦达定理
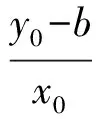
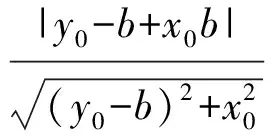


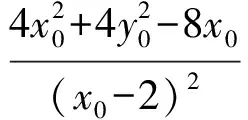


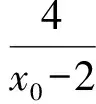
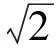
4 利用参数方程

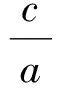


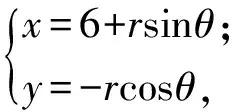

5 利用坐标方法