超声速导弹的自适应滑模动态面控制

赵红超, 史贤俊, 杨秀霞

(1.海军航空工程学院 703教研室, 山东 烟台 264001;2.海军航空工程学院 301教研室, 山东 烟台 264001)

超声速导弹的自适应滑模动态面控制

赵红超1, 史贤俊2, 杨秀霞2

(1.海军航空工程学院 703教研室, 山东 烟台 264001;2.海军航空工程学院 301教研室, 山东 烟台 264001)

为了提高超声速导弹过载控制系统的快速性,提出了一种自适应滑模动态面控制方法,并采用该方法进行了过载控制系统的设计。通过引入虚拟控制量,该方法克服了内外环设计中需要划分快、慢变量的缺点,提高了过载控制系统的跟踪速度。同时,对系统中存在不确定量的情况进行了研究,采用自适应滑模控制算法对不确定量的边界进行了估计,保证了整个闭环系统的渐近稳定性。仿真结果表明,所提出的自适应滑模动态面控制方法具有良好的控制性能。

超声速导弹; 快速性; 动态面控制; 自适应滑模控制

引言

世界各军事强国对导弹的战术技术性能要求越来越高,如超声速甚至高超声速飞行能力、大空域或小空域的高机动能力等。为了满足这些高性能要求,过载控制方法在导弹控制系统设计中得到了广泛应用。但是,对于尾控型导弹而言,从控制舵偏角到导弹过载输出之间的动力学存在非最小相位特性[1-2]。从控制系统设计的角度来看,非最小相位特性是不可接受的,它会引起系统内部动态的不稳定。因此,国内外控制领域研究者进行了大量的研究,提出了几种改进形式的过载控制系统设计以解决非最小相位问题。其中,应用比较广泛的就是内外环形式的过载控制系统[3-4],它在内环上对角速度进行控制,借助角速度实现外环上对过载的控制;由于从控制舵偏角到导弹角速度输出之间的动力学为最小相位,因此克服了非最小相位问题。

内外环设计思想尽管能够有效地解决非最小相位问题,但是它将角速度作为快变量,而过载作为慢变量,则过载控制系统对过载指令信号的跟踪速度要比对角速度指令的跟踪速度慢得多,这就限制了过载控制系统的快速性,快速性不高则会影响超声速导弹的机动性。为此,本文采用自适应滑模动态面控制方法来设计过载控制系统。通过引入虚拟控制量的概念,避免了需要划分快、慢变量的缺点。动态面控制方法是在Backstepping设计方法的基础上为了克服计算膨胀问题而发展起来的,是一种很有效的非线性控制系统设计方法[5-7]。针对动态面控制器设计中存在不确定量的问题,采用自适应滑模控制算法对不确定量的边界进行估计,保证了闭环控制系统的稳定性。将自适应滑模控制算法和动态面控制方法有机结合,本文提出了一种自适应滑模动态面控制方法。

1 超声速导弹的过载控制模型

以尾控型侧滑转弯(STT)超声速导弹为研究对象,导弹具有轴对称气动外形,其俯仰通道和偏航通道是基本一致的,因此,以俯仰通道为例进行研究。俯仰通道的模型如下:

(1)

式中各符号的物理意义见文献[8]。

考虑舵系统的一阶动态特性如下:

(2)

式中,τ为舵系统的时间常数;kδ为舵系统的增益;uc为控制输入。

综合式(1)和式(2),为了设计过载控制系统,需要做如下的状态变换:[αωzδz]T→ [nyωzδz]T。因此,俯仰通道的过载控制模型为:

(3)

x=[x1x2x3]T=[nyωzδz]T

则过载控制模型变换为:

(4)

系统输出量y=x1,被控输入量为uc。

2 自适应滑模动态面控制器设计

由式(4)可知,导弹模型为3阶系统,则控制器的递推设计包括3步。

第1步:考虑式(4)的第1个方程,定义误差面为s1=x1-x1d,其中,x1d为过载指令信号,是一个连续函数。则:

(5)

为了进一步分析,做如下假设:不确定量Δ1为有界的,但是其上界未知,即:

|Δ1|≤ρ1

(6)

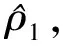
将x2作为虚拟控制量,并选取其期望值为:

(7)

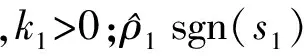
(8)

选取Lyapunov函数如下:

(9)

(10)

(11)

考虑式(4)的第2个方程,定义第2个误差面为s2=x2-x2d,则:

(12)

将x3作为虚拟控制量,选取其期望值为:

(13)

式中,k2>0。选取Lyapunov函数如下:

(14)

(15)

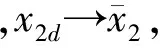
(16)

考虑式(4)的第3个方程,定义第3个误差面为s3=x3-x3d,则:

(17)

选取被控输入量为:

(18)

式中,k3>0。选取Lyapunov函数如下:

(19)

对式(19)求导并将式(17)、式(18)代入,可得:

(20)

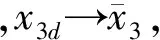
总结上述设计过程可知,所提出的自适应滑模动态面控制器的模型为:

(21)

本文只考虑了式(4)的第1个方程中含有不确定量的情形,显然,考虑第2和第3个方程中也含有不确定量时,上述设计过程只需做简单修改便可以设计出稳定的控制器。

3 数字仿真

以某型超声速反舰导弹为研究对象,对其低空飞行时俯仰通道的过载控制系统进行仿真,以检验所提出的自适应滑模动态面控制方法的控制效果。选取过载指令信号分别为大小两种阶跃信号,大信号的值为x1d=5.0,小信号的值为x1d=0.1。通过仿真调试,确定一组控制器参数为:k1=8,λ1=0.6,τ2=0.010 s,k2=12,τ3=0.005 s,k3=4,对大小指令信号都适用。仿真结果分别如图1、图2所示。

图1描述了当指令信号为大信号时导弹过载的跟踪曲线,此时调节时间为0.43 s;图2描述了当指令信号为小信号时导弹过载的跟踪曲线,此时调节时间为0.18 s。无论是大信号还是小信号,最终的跟踪精度都达到了100%。

图1 导弹过载对大信号的跟踪曲线

图2 导弹过载对小信号的跟踪曲线

上述仿真结果表明,所设计的自适应滑模动态面控制器能够使导弹快速而准确地跟踪指令信号的变化,具有较好的控制性能。

4 结束语

前人研究的内外环形式的过载控制系统需要划分快、慢变量,不利于提高超声速导弹的快速性和机动性。本文提出了一种自适应滑模动态面控制方法,应用该方法设计了过载控制系统。设计过程中引入了虚拟控制量和自适应滑模控制算法,解决了过载控制系统快速性不高的问题,而且克服了不确定量的影响,保证了控制系统的渐近稳定性。通过理论分析和数字仿真,证明了所提出的方法是很有效的。本文的研究为超声速导弹的过载控制系统设计提供了新思路、新方法,对提高超声速导弹的战术技术性能具有重要意义。不过,本文仅进行了单个特征点的仿真分析,为了促进该方法的工程应用,进一步的工作需要以超声速导弹的六自由度非线性模型为研究对象,应用该方法进行导弹全弹道飞行的仿真分析。

[1] 顾文锦,赵红超,邓以高.反舰导弹控制中的稳定性研究[J].飞行力学,2005,23(2):51-55.

[2] 陈洁,顾文锦,周绍磊.基于二阶滑模的导弹控制系统设计[J].北京航空航天大学学报,2009,35(3):332-335.

[3] Adounkpe I J,Godoy E,Harcaut J P.Robustness analysis of a nonlinear missile autopilot: an integral quadratic constraint approach[OL].http://ascc2004.ee.mu.oz.au/proceedings/papers/P266.pdf,2004.

[4] Astrov I,Tatarly S,Tatarly S.Simulation of missile autopilot with two-rate hybrid neural network system[J].Advances in Electrical and Computer Engineering,2007,7(1):18-21.

[5] Yoo S J,Park J B,Choi Y H.Output feedback dynamic surface control of flexible-joint robots[J].International Journal of Control,Automation,and Systems,2008,6(2):223-233.

[6] Hou M Z,Duan G R.Adaptive dynamic surfac control for integrated missile guidance and autopilot[J].Intrnational Journal of Automation and Computing,2011,8(1):122-127.

[7] 贾涛,刘军,钱富才.一类非线性时滞系统的自适应模糊动态面控制[J].自动化学报,2011,37(1):83-91.

[8] 钱杏芳,林瑞雄,赵亚男.导弹飞行力学[M].北京:北京理工大学出版社,2000:175-177.

(编辑：姚妙慧)

Adaptivesliding-modedynamicsurfacecontrolforsupersonicmissile

ZHAO Hong-chao1, SHI Xian-jun2, YANG Xiu-xia2

(1.Faculty 703, Naval Aeronautical and Astronautical University, Yantai 264001, China;2.Faculty 301, Naval Aeronautical and Astronautical University, Yantai 264001, China)

In order to improve speediness of overload control system of a supersonic missile, this paper presents an adaptive sliding-mode dynamic surface control approach. The overload control system of a supersonic missile is designed by this approach. With the introducing of virtual control variables in this approach, this approach overcomes the disadvantage of partitioning fast and slow variables in the inner-outer loop design, and the tracking speed of the overload control system is increased. The case of the system having uncertainty is researched. The adaptive sliding-mode control approach is adopted to estimate the bound of uncertainty, which ensures the asymptotic stability of the whole close-loop system. Simulation results show that the presented adaptive sliding-mode dynamic surface control approach has good control performance.

supersonic missile; speediness; dynamic surface control; adaptive sliding-mode control

TJ765

A

1002-0853(2012)05-0432-04

2011-11-16;

2012-03-26

国家自然科学基金资助(61174031)

赵红超(1975-)，男，河北定州人，讲师，博士，主要从事飞行器控制理论与变轨技术研究。