高超声速飞行器高阶滑模控制器设计

张园园, 胡杨, 刘志敏, 李仁府,3

(1.华中科技大学 航空航天研究中心, 湖北 武汉 430074;2.沈阳飞机设计研究所 总体设计部, 辽宁 沈阳 110035;3.华中科技大学 数字制造装备与技术国家重点实验室, 湖北 武汉 430074)

高超声速飞行器高阶滑模控制器设计

张园园1, 胡杨1, 刘志敏2, 李仁府1,3

(1.华中科技大学 航空航天研究中心, 湖北 武汉 430074;2.沈阳飞机设计研究所 总体设计部, 辽宁 沈阳 110035;3.华中科技大学 数字制造装备与技术国家重点实验室, 湖北 武汉 430074)

针对高度非线性、强耦合、参数不确定性的高超声速飞行器纵向运动数学模型,设计了一种基于Quasi-continuous高阶滑模理论的控制器,并与传统滑模控制器进行了分析和比较。仿真结果表明,Quasi-continuous高阶滑模控制在高度阶跃响应时间上比传统滑模控制减少了30%,速度阶跃响应时间比传统滑模控制减少了约56%。说明所设计的控制器能较好地满足在极端环境中飞行的高超声速飞行器对控制指令响应时间的要求。因此,该项研究对高超声速飞行器控制系统的设计有十分重要的参考价值。

高超声速飞行器; Quasi-continuous高阶滑模控制; 精确线性化

引言

高超声速飞行器在高海拔和大马赫数的飞行环境中,空气密度、飞行器速度及机体质量等变化较大。此外,高超声速飞行器在飞行过程中还受到结构振动、动力推进、空气动力耦合及不确定性影响,这使得其模型具有高度非线性、不确定性和强耦合性等特点[1-3]。因此,其对控制系统的要求十分苛刻,飞行控制技术也一直是高超声速飞行器研究中的重点及难点。

近年来,许多现代控制理论和方法都应用到高超声速飞行器的制导与控制中,如动态逆控制、最优控制、模糊逻辑控制、神经网络控制、遗传算法以及将这些控制方法相结合的控制[4-8]。为了适应控制对象的参数变化和外界环境扰动等因素的影响,高超声速飞行器控制系统需要具有很强的鲁棒性,滑模变结构控制在这方面显示出了优越的性能[9-10]。高阶滑模控制理论是基于高阶滑模模态的设计,高阶滑动模态不仅比一阶滑动模态更接近系统的物理本质,而且具有更高的精度和动态性能。Levant基于非线性方程齐次理论设计了有限时间内收敛的任意阶高阶滑模控制算法(HOSMC)及Quasi-continuous HOSM控制算法,其思想是将不连续的反馈控制输入作用在滑动模态的高阶导数上[11],所设计的控制器对系统的不确定性具有较强的鲁棒性和较高的精度。

但是,在高超声速飞行器控制领域对高阶滑模理论的应用还很少。本文以NASA兰利实验室提供的高超声速飞行器运动模型作为研究对象,探索Quasi-continuous高阶滑模控制策略在高超声速飞行器纵向运动控制系统中的应用,旨在为解决高超声速飞行器非线性模型的控制问题开发一种新的控制器设计方法,最后通过仿真与传统滑模控制进行了比较。

1 纵向模型

高超声速飞行器纵向模型用非线性微分方程表示如下[4,9]:

其中:

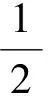
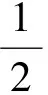
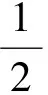
本文中:

CL=0.6203α

CD=0.645α2+0.0043378α+0.003772

CM(α)=-0.035α2+0.036617α+5.3216×10-6

0.3015α-0.2289)

CM(δe)=0.0292(δe-α)

ρ=1.2266e-h/7315.2

高超声速飞行器发动机等效于一个二阶系统模型:

式中,取l1=l2=0,l3=1;β为发动机节流阀调定,与发动机燃烧率和推力系数有关。

控制输入为[δe,βc]T,控制输出为[v,h]T,因此高超声速飞行器纵向模型可以看成一个两输入两输出的非线性强耦合系统。用精确化方法线化高超声速飞行器纵向模型可得到:

(1)

式中,各参数详细表示见文献[10-11]。

2 传统滑模变结构控制

以跟踪期望输出量[vd,hd]为目的,选择如下两个滑模面[4,9]:

设计如下传统的滑模控制趋近律[4]:

ki>0 (i=1,2)

可以得到高超声速飞行器纵向模型飞行控制律为:

3 Quasi-continuous高阶滑模控制

为了跟踪输出信号vd,hd,设计如下两个滑模面:

Sv=v-vd,ev(t)=v-vd

Sh=h-hd,eh(t)=h-hd

可以得到如下控制器:

(2)

为了让滑模面在有限的时间里趋近零,可以采用如下三阶和四阶Quasi-continuous滑模控制器[11]:

(3)

(4)

4 纵向模型的模拟仿真

4.1 Quasi-continuous高阶滑模控制器参数的选取

式(3)和式(4)中的参数αv,αh的取值会极大地影响系统的响应时间,本文通过系统闭环动态响应仿真来考察αv,αh的取值对系统响应带来的影响,并以此仿真结果作为选取参数的标准。

联合式(1)和式(2),可得如下闭环动态方程:

图1为速度的闭环动态响应。由图1可知,当αv<10时,系统的稳定性将得不到保证;当αv>100后,输出响应的超调量几乎不变。因此,仿真中取αv=100。

图1 速度的闭环动态响应图

图2为高度的闭环动态响应。由图2可知,αh≤7后,系统已经不稳定了。增大αh的值,超调量变化不明显,反而稳定时间改变较大。另外,显然随着αh的增大,稳定时间有所增加。因此选取αh=10。

图2 高度的闭环动态响应图

4.2 模拟仿真

对于传统滑模变结构控制器设计[9],其参数为:λ1=λ2=0.5,k1=k2=2。对于Quasi-continuous高阶滑模变结构控制,其参数为:αv=100,αh=10。其它的气动参数和相关数据来源于文献[4,10]。在高超声速飞行器的平衡飞行条件(v0=4 590.3 m/s,h0=33 528 m,α0=2.745°,δe0=-0.55°,βc0=0.21°)下,分别给定飞行高度增量和飞行速度增量的指令为hd=100 m,vd=100 m/s。

图3～图6为系统在输入指令作用下的输出响应。由图可知,在给定高度和速度输入指令下,传统滑模控制和Quasi-continuous高阶滑模控制都能跟踪输入的飞行高度和飞行速度指令信号,但是后者响应明显比前者快得多。由图3可知,在给定高度增量为100 m时,两种控制的高度响应时间分别为15 s 和21 s,可见后者比前者提高了近30%。由图5可知,在给定速度增量为100 m/s时的速度响应时间分别为10 s和23 s,可见后者比前者提高了56%。如图4和图6所示,高阶滑模控制也显示出了明显的优势,高度和速度响应都在0.5 s内稳定在零值,而传统滑模控制都在10 s以后稳定到零值。由图4可知,标准滑模振荡量级为10-3,稳定时间在16 s左右;高阶滑模振荡量级为10-4,稳定时间小于0.5 s。由图6可知,传统滑模稳定时间约为31 s,振荡幅度为10-2;高阶滑模稳定时间约为11 s,振荡幅度为10-3。

图3 hd=100 m时的高度变化响应

图4 hd=100 m时的速度响应

图5 vd=100 m/s时的速度响应

图6 vd=100 m/s时的高度响应

由上述仿真结果分析可知,用Quasi-continuous高阶滑模理论对高超声速飞行器进行控制器设计,能够精确地跟踪速度和高度输入指令,与传统滑模控制相比,其响应时间也得到了很大的改善。因而,能够更好地满足高超声速飞行器在大马赫数和高海拔条件下快速机动飞行的要求。

5 结束语

高超声速飞行器在飞行过程中,空气密度及飞行速度变化很大,动力学参数变化剧烈,通道间的耦合作用非常严重,即表现出强烈的多变量耦合和非线性。本文采用精确线性化方法将高超声速飞行器非线性的纵向模型进行了完全线性化,同时用动态逆方法对其解耦,进而用Quasi-continuous高阶滑模控制算法对控制器进行设计。从飞行高度和飞行速度指令信号的响应结果来看,Quasi-continuous高阶滑模控制算法不仅精度高,而且能够快速地跟踪指令信号,与传统的滑模控制相比,显示出了明显的优势,能够很好地满足高超声速飞行器快速机动作战的要求。

[1] 朱云骥,史忠科.高超声速飞行器飞行特性与控制的若干问题[J].飞行力学,2005,23(3):5-8.

[2] 吴宏鑫,孟斌.高超声速飞行器控制研究综述[J].力学进展,2009,39(6):1-3.

[3] 杨亚政,李松年,杨嘉陵.超声速飞行器及其关键技术简论[J].力学进展,2007,37(4):537-555.

[4] Wang Q,Stengel R F.Robust nonlinear control of a hypersonic aircraft [J].Journal of Guidance,Control,and Dynamics,2000,23(4):577-585.

[5] Gibson T E,Annaswamy A M.Adaptive control of hypersonic vehicles in the presence of thrust and actuator uncertainties [R].AIAA-2008-6961,2008,1-16.

[6] Austin K J,Jacobs P A.Application of genetic algorithms to hypersonic flight control[C]//IFSA World Congress and 20th NAFI-PS International Conference.Australia,2001:2428-2433.

[7] Wu S F,Engelen J H,BabuSka R.Intelligent flight controller design with fuzzy logic for an atmospheric re-entry vehicle [R].AIAA-2000-174,2000.

[8] Fiorentini L,Serrani A,Bolender M A.Nonlinear robust adaptive control of flexible air-breathing hypersonic vehicle[J].Journal of Guidance,Control,and Dynamics,2009,32(2):401-415.

[9] Xu H J,Mirmirani M D,Ioannou P A.Adaptive sliding mode control design for hypersonic flight vehicle[J].Journal of Guidance,Control,and Dynamics,2004,27(5):829-831.

[10] 刘燕斌,陆宇平.基于变结构理论的高超声速飞行器纵向逆飞行控制[J].信息与控制,2006,35(3):1-3.

[11] Levant A.Quasi-continuous high-order sliding mode controllers[J].IEEE Transatctions on Automat Control,2006,50(11):1812-1816.

(编辑：姚妙慧)

Designofhigh-orderslidingmodecontrollerforhypersonicvehicle

ZHANG Yuan-yuan1, HU Yang1, LIU Zhi-min2, LI Ren-fu1,3

(1.Research Center of Aeronautics and Astronautics, Huazhong University of Science and Technology, Wuhan 430074, China;2.General Desingn Department, Shenyang Aircraft Design and Research Institute, Shenyang 110035, China;3.State Key Lab of Digital Manufacturing Equipment and Technology, Huazhong University of Science and Technology, Wuhan 430074, China)

This paper proposes a Quasi-continuous high-order sliding mode controller (QHOSMC) to deal with highly nonlinear, tightly coupled longitudinal mathematic model with parametric uncertainty for a hypersonic vehicle. The characteristics of this proposed mode are analyzed. Compared the simulation results by QHOSMC with those by conventional sliding mode, it is found that the time response to step-altitude and step-velocity command input decreases by 30 percent and 56 percent, respectively. This observation shows the QHOSMC method could have great significance for the design of hypersonic vehicle flight control system.

hypersonic vehicle; Quasi-continuous high-order sliding mode control; accurate linearization

V249.1

A

1002-0853(2012)05-0414-04

2011-11-21;

2012-04-19

张园园(1986-)，女，河南确山人，博士研究生，研究方向为飞行控制与仿真。