模型逆控制在非线性IFPC系统中的应用

樊战旗, 刘林, 纪多红

(1.西北工业大学 自动化学院, 陕西 西安 710072;2.西安飞行自动控制研究所 飞控部, 陕西 西安 710065)

模型逆控制在非线性IFPC系统中的应用

樊战旗1, 刘林1, 纪多红2

(1.西北工业大学 自动化学院, 陕西 西安 710072;2.西安飞行自动控制研究所 飞控部, 陕西 西安 710065)

研究了模型逆控制方法应用于IFPC一体化控制器的设计问题。简要介绍了模型逆非线性控制方法的概念、特点。在此基础上,将模型逆与经典控制相结合,设计了IFPC控制律,并进行了时域仿真与飞行品质分析。结果表明,所设计的控制律无需增益调参即可实现各状态的指令跟踪,并具有较强的鲁棒性能;系统具有典型的一阶/二阶动态特性,满足一级飞行品质要求。

IFPC; 非线性模型逆; 飞行控制律设计; 飞行品质分析; 等效拟配

引言

为实现新一代战机超机动性和高敏捷性,迫切要求采用综合飞行/推进控制(IFPC)技术,同时由于IFPC系统中存在大量的非线性,又加剧了新一代战机的IFPC系统设计的难度,传统的线性设计方法已很难设计出满足要求的控制器[1],对非线性系统控制方法的研究是实现上述目标的必由之路。

研究较为广泛的非线性控制方法是非线性变换技术,该方法基于非线性系统的坐标变换,将一个非线性系统变换成线性系统。由于线性化过程需要得到非线性系统的逆模型,从逆模型和控制的角度来看,该方法可称作“模型逆控制”[2]。在模型逆控制中,通过直接分析对模型求逆。若考虑了整个模型的动态特性进行逆变换,则是“动态逆控制”;若仅对稳态时的模型求逆或是忽略动态过程而求逆,则是“稳态逆控制”。本文在IFPC系统设计过程中,在充分考虑系统特点的基础上,通过两种方法的有机结合,设计了IFPC控制律。

1 模型逆方法简述

1.1 动态逆方法

设有系统:

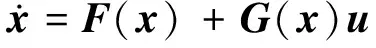
(1)

若G(x)可逆,令:

u=G-1(x)[ωc(xc-x)-F(x)]

(2)

式中,ωc为频带带宽;xc为指令;x,u分别为状态变量和输入。

则系统有外特性:

(3)

显然,如果模型式(1)是精确的,则系统式(3)是稳定的,系统的跟踪误差将渐近收敛到零。

动态逆方法设计复杂性低,但该方法基于精确数学模型,不能提供严格的性能,也不能保证鲁棒稳定性。将其与其他控制方法相结合进行联合控制,提高系统的抗干扰及模型不确定性能力,已成为新的研究热点[3]。

1.2 稳态逆方法

稳态逆方法可以视为动态逆方法的特例或简化,它不考虑系统的动态特性,如1.1节中的系统,稳态逆控制时,可认为：

0=F(x)+G(x)u

(4)

若G(x)可逆,则有:

u=-G-1(x)F(x)

(5)

显然相对于其他非线性控制方法,稳态逆控制具有计算量小、直观性强的优点。

2 IFPC控制律设计

2.1 控制策略

控制增稳系统大都是“指令-响应(迎角、侧滑角和绕机体的滚转角速度)”的形式,但在大迎角情况下,这种形式的横向控制策略就存在较大的弊端。此种情况下的滚转角、迎角和侧滑角呈正弦型变化。当滚转角为90°时,迎角变成侧滑角。尤其在大迎角情况下,将造成不允许的大的俯仰、滚转和偏航力矩,以及载荷系数的强烈变化,这是很难控制的。由于升力、阻力和侧力也呈周期性变化,所以飞行航迹也受到强烈影响[4]。

鉴于如上考虑,本文通过模型逆方法设计控制律,驾驶员操纵指令和引导变量之间的配置如下:操纵杆Fx→绕速度轴的滚转角速度ωxa;操纵杆Fz→迎角α；脚蹬Fy→侧滑角β。

基于层叠结构思想,本文快回路为角速度控制回路,慢回路为迎角和侧滑角控制回路,极慢回路为速度回路。其中快回路和极慢回路控制通过动态逆方法实现,慢回路通过“稳态逆+PI”实现,控制律结构图如图1所示。

图1 控制律结构示意图

2.2 快回路设计

本文设计的快回路,控制目标为绕速度轴的偏转角速度。由于传感器只测得绕机体轴的偏转角速度,因此必须根据如下转换关系,把期望的绕速度轴偏转的角速度转换到绕体轴系的角速度。

(6)

系统的内回路对应于飞机的力矩方程,对飞机力矩方程进行整理,可得:

(7)

其中:

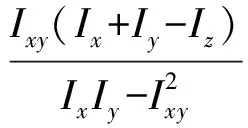
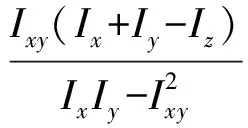
在设计控制律时,式(7)的左边为期望的角加速度,由外回路控制律计算得到。由于滚转角速度是直接指令响应对象,期望能精确跟踪,因此选择比例积分形式,其他选择比例形式。因此有下式:

式中,K1x,K1y,K1z为各通道的比例环节系数;K2x为滚转通道的积分环节系数;ωxc,ωyc,ωzc为外回路控制律或指令解算给出的角速度指令。

由于G1可逆,因此根据动态逆理论,内回路的控制律为:

2.3 慢回路设计

慢回路要控制的是迎角、侧滑角变量。由于空速主要由推力控制,属于极慢状态量,所以在这种关系中,空速可视为常值。在设计慢回路控制律时,采用稳态逆控制方法。

利用下式把期望角度αc和βc首先换算成等效的预置变量nzac和nyac(气流坐标系上的载荷系数):

为了把这些量换算成响应的转动角速度,同样还要采用力方程,这里假定速度不变,迎角和侧滑角皆为小量。按照公式可推导出：

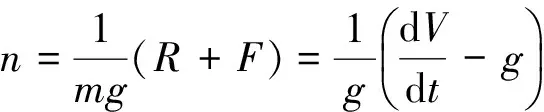
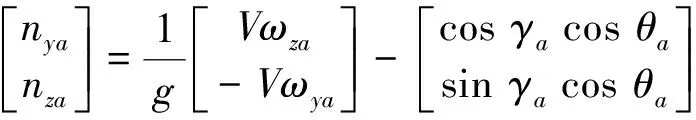
从而可变换成:

稳态逆控制方法没有引入动态环节,此时仿真动态特性差,指令跟踪慢,不能满足飞行品质要求。因此,需另外适当引入动态环节。本文通过结合经典PI控制来实现控制。该PI控制直接计算出期望的舵偏指令,与快回路计算得到的舵偏指令相叠加,得到最终的控制舵偏指令。

2.4 极慢回路设计

该回路通过“推力-V”来控制,发动机采用简化的一阶模型,并根据飞行状态对最大推力进行限幅,回路控制律通过动态逆方法来求取。由于速度控制没有追求完全精确跟踪的必要,因此本文仅采用比例方法。求取过程与快回路相同,最终可得控制律为:

Pd=G2-1[KV(Vc-V)-f2]

其中:

G2=gcosαcosβ

f2=g{[(Ysinα+Qcosα)cosα-

(Ycosα-Qsinα)sinα]}cosβ+

nzsinβ-[cosβ(cosαsin ϑ-

sinαcos ϑ cosγ)-sinβsinγcos ϑ]

式中,KV为该通道的比例环节系数;Vc为希望的速度指令。

至此,完成了全部的IFPC控制律设计。

3 控制律仿真与飞行品质分析

3.1 时域仿真

本文选择0506(05表示飞行高度为5 km, 06表示Ma=0.6,下同)状态进行时域仿真,输入为迎角5°、侧滑角3°、滚转角速度10(°)/s的阶跃指令。为检验控制系统的鲁棒性,对飞机仿真中的气动数据进行扰动,以此来检验动态逆控制律的性能。将飞机模型数据中的三轴力和力矩系数同时增大到原参数的1.5倍,又将力和力矩系数同时减小到原参数的0.7倍,得到的时域响应结果如图2～图5所示。图中,实线为模型不摄动,虚线为系数放大为原来的1.5倍,点线为系数减小到原系数的0.7倍。

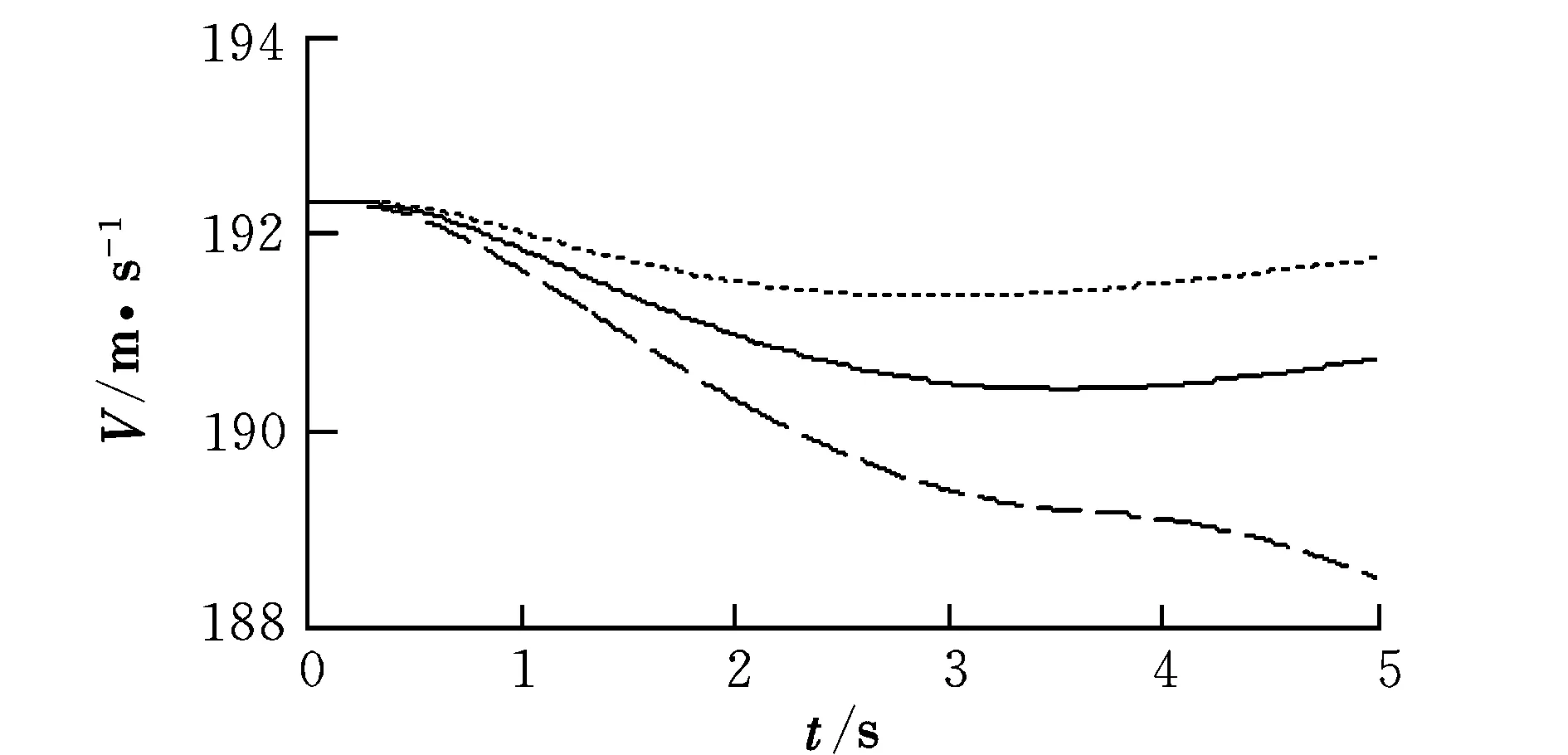
图2 飞行速度仿真曲线

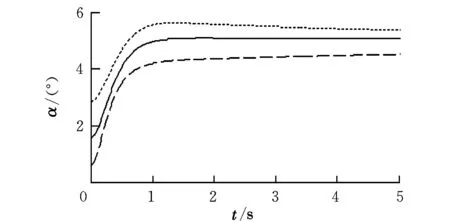
图3 迎角仿真曲线

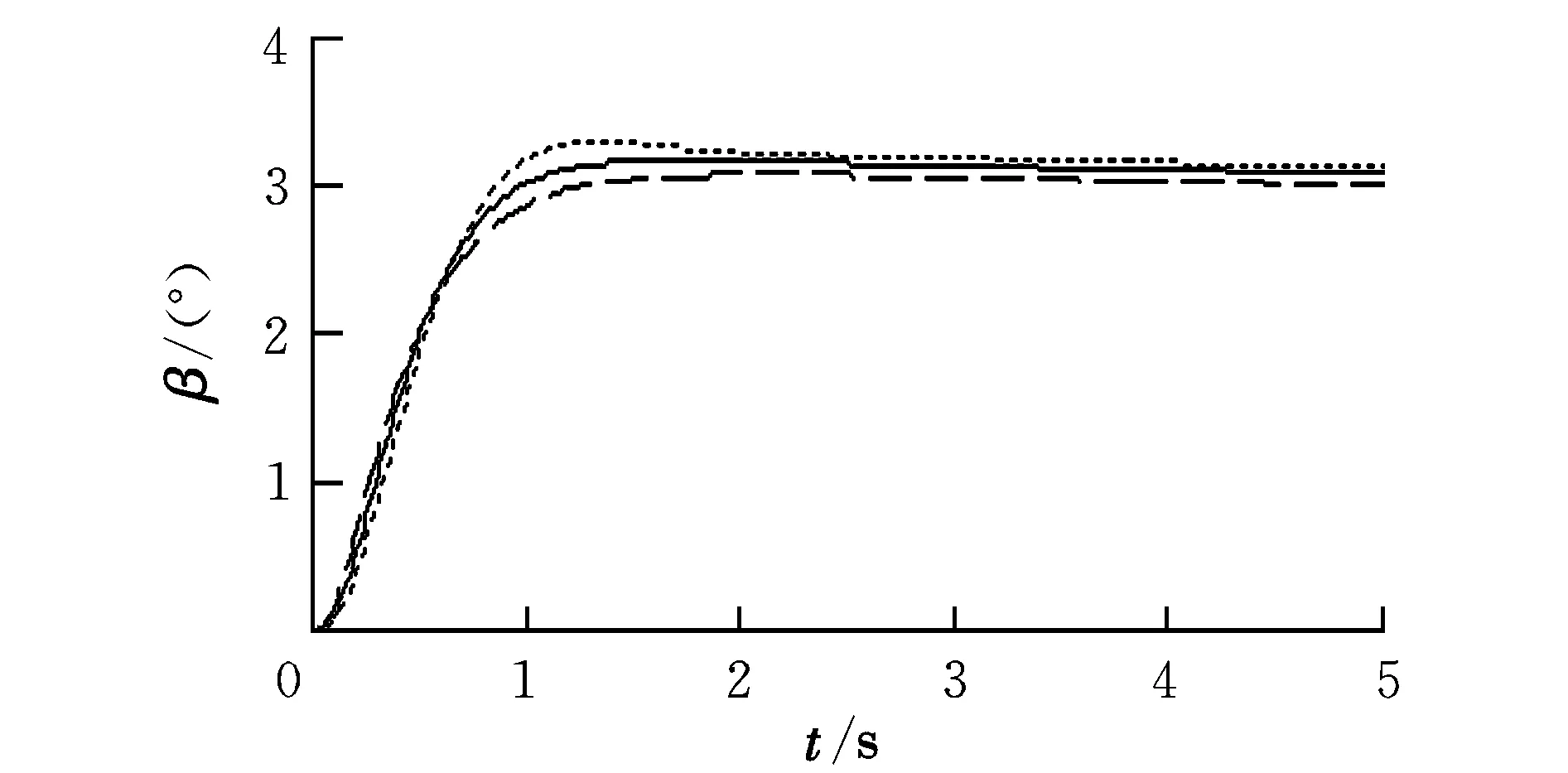
图4 侧滑角仿真曲线

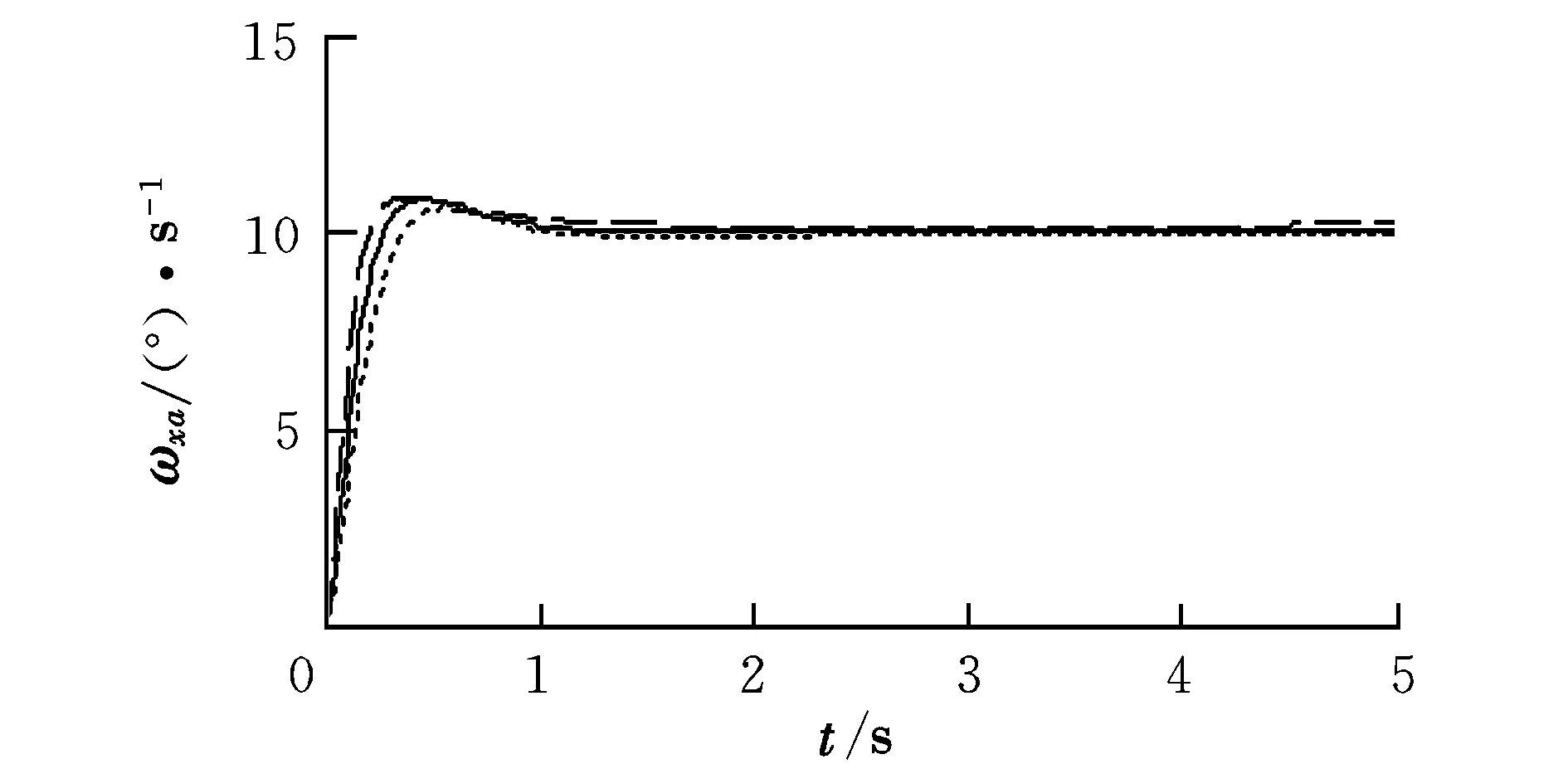
图5 滚转角速度仿真曲线

由仿真结果可看出,设计的控制律能实现指令的精确跟踪,同时对于模型的摄动具有很好的鲁棒性。

3.2 频域分析

3.2.1频域等效拟配

由于控制律及飞机对象均为非线性的,所以采用傅立叶变换的方法进行频域仿真,再将频域结果进行等效拟配,得到需要的拟配结果。

纵向、航向、横向的等效形式分别为:

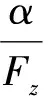
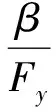
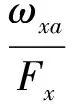
在飞行包线内,首先基于0506状态点进行等效拟配,结果如图6～图8所示。图中,实线为傅立叶变换结果,点线为拟配的等效曲线。然后给出一些典型状态点的拟配结果,如表1～表3所示。

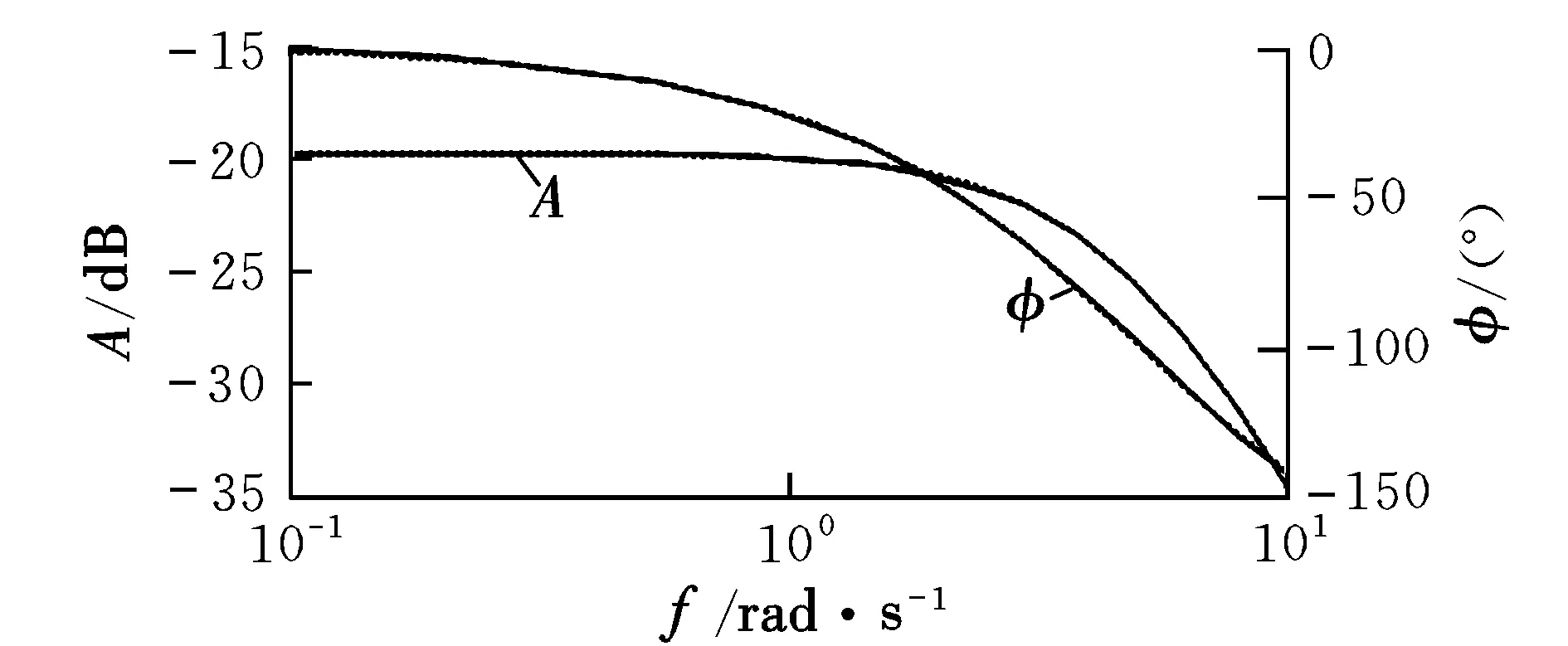
图6 纵向频域仿真及等效拟配结果

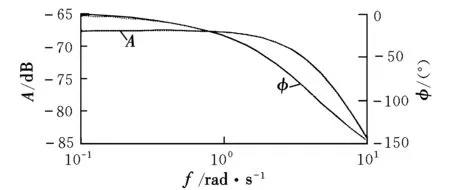
图7 航向频域仿真及等效拟配结果

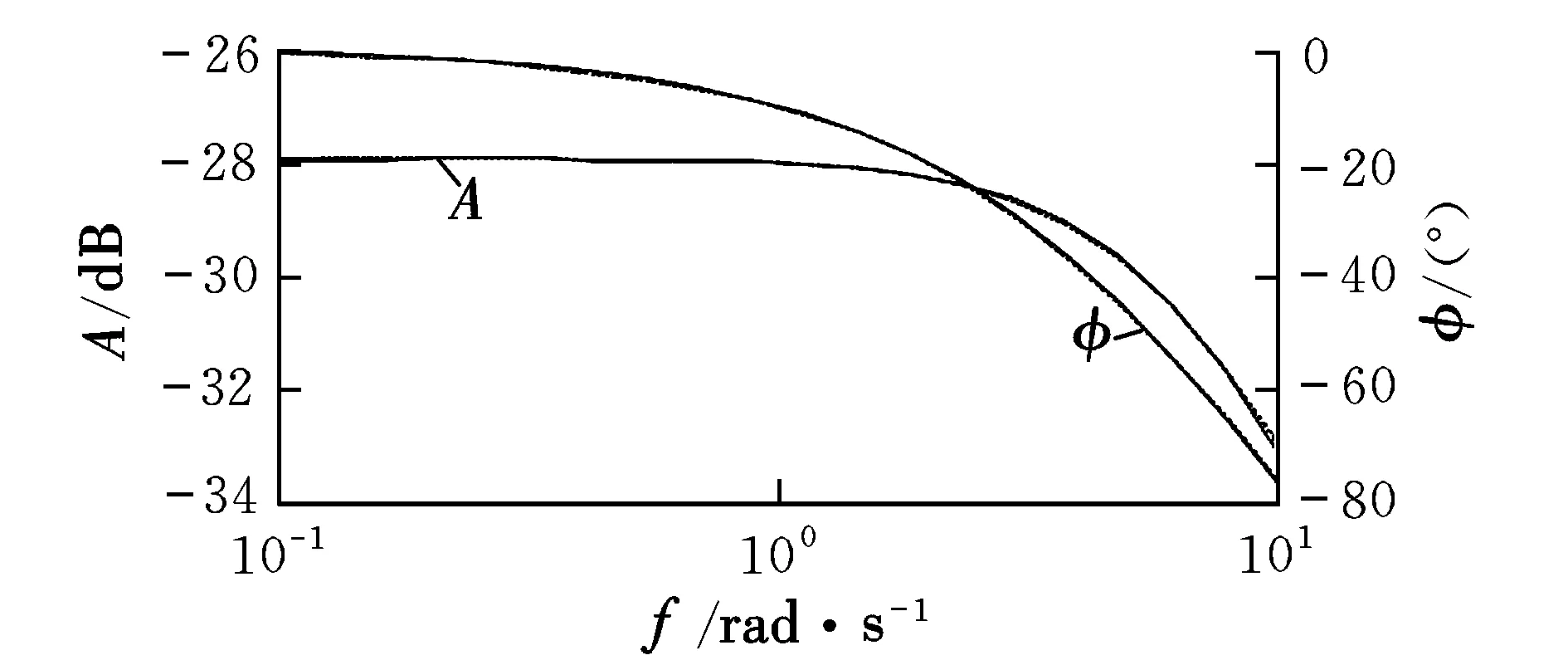
图8 横向频域仿真及等效拟配结果

表1纵向频域等效拟配结果

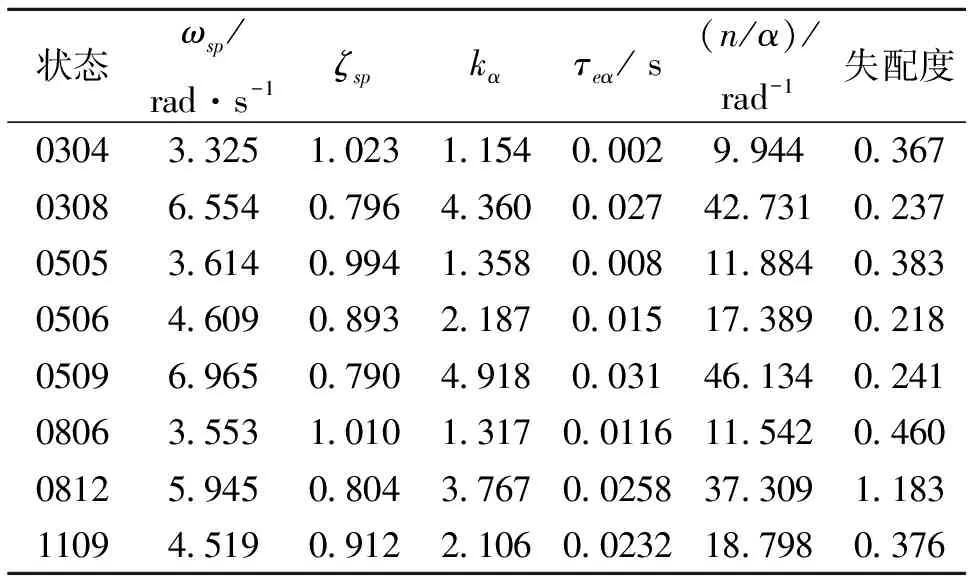
状态ωsp/rad·s-1ζspkατeα/s(n/α)/rad-1失配度03043 3251 0231 1540 0029 9440 36703086 5540 7964 3600 02742 7310 23705053 6140 9941 3580 00811 8840 38305064 6090 8932 1870 01517 3890 21805096 9650 7904 9180 03146 1340 24108063 5531 0101 3170 011611 5420 46008125 9450 8043 7670 025837 3091 18311094 5190 9122 1060 023218 7980 376

表2 航向频域等效拟配结果

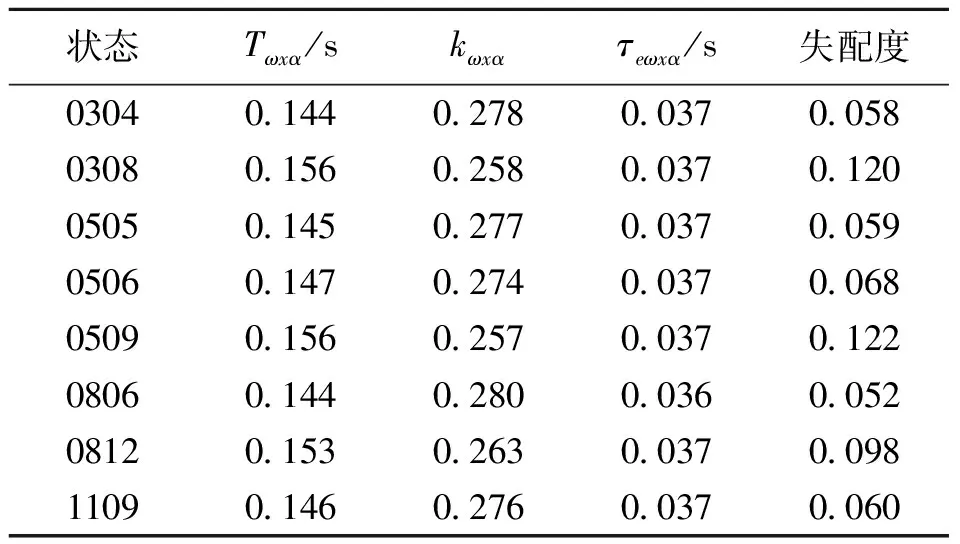
表3 横向频域等效拟配结果

从表1～表3拟配结果可知,所设计的控制器亦能很好地应用于飞行包线内的其他状态点。

3.2.2飞行品质分析

根据表1～表3,由GJB185-86可得品质结果如下:

(1)纵向:①等效短周期阻尼比在0.35～1.30之间,为一级品质;②等效时延τeα<0.1 s,为一级品质;③短周期俯仰响应 (CAP准则),为一级品质。

(2)横航向:①等效荷兰滚频率和阻尼:各状态均为一级;②滚转时间常数:为一级品质;③等效时延:为一级品质。

4 结束语

基于模型逆控制方法,结合经典控制,设计了IFPC控制律,避免了传统方法的增益调参,同时也解决了动态逆方法计算量大、对模型精确程度要求高的问题。尤为重要的是,采用该方法设计的控制系统,具有典型的一阶/二阶动态特性,完全满足一级飞行品质要求。

[1] Snell S A,Enns D F,Garrard W L.Nonlinear control of a super maneuverable aircraft[R].AIAA 89-3486-cp,1989.

[2] 刘波,何清华,邹湘伏.无人机飞行控制技术初探[J].飞行力学,2007,25(2):5-8.

[3] Magni J-F,Bennani S,Terlouw J.Robust flight control: a design challenge[M].London:Springer-Verlag,1997:102-111.

[4] 鲁道夫·布罗克豪斯.飞行控制[M].金长江,译.北京:国防工业出版社,1999:515-536.

(编辑：姚妙慧)

ApplicationofmodelinversioncontrolinnonlinearIFPCsystem

FAN Zhan-qi1, LIU Lin1, JI Duo-hong2

(1.College of Automation, NWPU, Xi’an 710072, China;2.Department of Flight Control, Flight Automatic Control Research Institute, Xi’an 710065, China)

This paper deals with the application of model inversion control method in IFPC systems. The concepts and characteristics of model inversion control method are introduced. On the basis of this, the IFPC control law through combination of model inversion and classical control is designed. Then, the time-domain simulation and flying quality analysis are given. The results show that the designed control law (FCL) can meet the tracking precision requirement without gain scheduling, and has a strong robustness to parametric disturbances; the IFPC system has first/second-order dynamic characteristics, which meets the requirements for the 1stlevel flying quality.

IFPC; nonlinear model inversion; FCL design; flying qualities analysis; equivalent match

V249.1

A

1002-0853(2012)05-0454-04

2011-12-14;

2012-05-20

航空科学基金资助(2010ZC18002)

樊战旗(1971-),男,陕西富平人,研究员,博士研究生,主要从事飞行控制系统设计、控制理论与应用研究。