基于变权重伪并行遗传算法的空战机动决策

张涛, 于雷, 周中良, 李飞

(1.空军工程大学 工程学院, 陕西 西安 710038;2.中国人民解放军 94831部队, 浙江 衢州 324001)

基于变权重伪并行遗传算法的空战机动决策

张涛1,2, 于雷1, 周中良1, 李飞1

(1.空军工程大学 工程学院, 陕西 西安 710038;2.中国人民解放军 94831部队, 浙江 衢州 324001)

针对空战机动决策中态势多样化对机动决策的影响以及控制量的细化问题,以敌我双机空战为背景,利用空战优势函数值作为空战机动决策的依据,基于滚动时域控制方法,采用变权重自适应伪并行遗传算法解决空战决策问题。重点分析了隐身优势函数以及变权重函数的建立、遗传编码方式、操作算子的确定,最后对空战决策进行了仿真。仿真结果验证了隐身优势函数的合理性,以及该理论在空战机动决策方面的有效性。

自适应伪并行遗传算法; 变权重; 机动决策; 优势函数

引言

当前,随着机载武器、传感器和飞机本身性能的不断提高,现代空战的空间范围不断扩大,目标、武器以及本机之间的相互关系也变得越来越复杂。为了减轻驾驶员的负担,提高空战效能,对空战机动决策的研究愈显重要[1]。针对现代空战的需求,世界各军事大国都在加紧空战机动决策及其生成技术的研究和应用开发。空战机动决策问题是NP(Nondeterministic Polynomial)难问题,目前解决此问题的方法有:神经网络法、影响图法、Petri网法、蚁群算法、粒子群算法等,其中神经网络法很难获得真实的空战数据来对神经网络进行学习训练,影响图法及蚁群算法的计算时间较长,难以满足空战的实时性要求,文献[2]提出了遗传算法在战术飞行动作决策方面的应用,将48种战术动作进行编码、遗传优化,但文中没有给出具体编码及仿真过程。目前国内的研究主要是依据典型机动动作库进行机动决策,没有考虑到控制量的细化问题。本文提出了基于滚动时域的控制方法,对具体控制量进行细化、离散化,采用变权重自适应伪并行遗传算法解决机动决策问题。

滚动时域方法的实质是用随时间反复进行的一系列小规模优化问题求解的过程取代一个静态的大规模优化问题求解的结果,以达到在优化的前提下降低计算量并适应不确定性变化的目的[3]。本文将空战过程分为多个时间阶段,利用滚动时域控制的理论进行求解[4],从而达到作战要求。

遗传算法(Genetic Algorithm,GA)是近年来迅速发展起来的一种基于遗传学进化思想的随机搜索优化算法[5-6]。该算法作为一种新的全局优化搜索算法[7],其具有隐含并行性和全局解空间搜索的特点[8]。自适应伪并行遗传算法将算法自身隐含的并行性及并行计算相结合,提高了优化计算效率、收敛速度,有效抑制了“早熟”现象[7]。

1 优势函数的建立

1.1 角度优势函数

角度优势函数主要与雷达最大探测角及空空导弹发射角有关,战斗机要进行搜索、跟踪及武器发射、制导,必须控制载机使目标在一定的角度范围内。因此角度优势函数表示为[9]:

(1)

式中,QI为我机速度矢量与目标线的夹角;αmax为空空导弹最大发射角;βmax为雷达最大探测角。S1取值范围为(0,1),取值越大,优势越大。

1.2 速度优势函数

速度优势函数为:

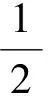
(2)

式中,VI为我机速度;VT为目标机速度;VmaxI,VmaxT,VminI,VminT分别为我机和目标机的最大、最小飞行速度。S2取值范围为(0,1),取值越大,优势越大。

1.3 隐身优势函数

由于飞机的雷达反射面积SRC决定了被发现的概率及攻击概率等,直接影响飞机的安全性,因此有必要引入隐身优势函数:

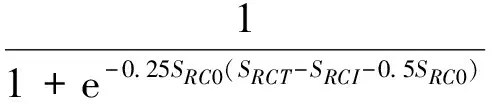
(3)

式中,SRC0为门限SRC差值;SRCT为目标机的雷达反射面积;SRCI为我机的雷达反射面积。S3取值范围为(0,1),取值越大,优势越大。

1.4 攻击优势函数

攻击优势函数的主要决定因素是载机所携带导弹的射程,射程与角度优势及隐身优势函数相关,因此攻击函数引入角度及隐身优势函数,攻击优势函数为:

(4)

式中,RI为我机机载空空导弹的射程;RT为目标机机载空空导弹的射程。S4取值范围为(0,1),取值越大,优势越大。

1.5 高度优势函数

高度优势函数为[10]:

(5)

式中,H为我机与目标机的相对高度差，我机在上为正;H0为门限高度差,其值随空战形式的不同而变化,可由决策者根据经验设定。S5取值范围为(0,1),取值越大,优势越大。

1.6 破坏跟踪函数

S6=

(6)

式中,ωT为目标机相对我机的角速度;αTmax为目标机最大雷达视场跟踪角;ωI为我机相对目标机的角速度。S6取值范围为(0,1),取值越大,优势越大。

1.7 综合优势函数及变权重的确定

空战态势是决策者进行空战决策的依据,空战样式及时间阶段的不同,对各优势函数的敏感度也就不同。为体现决策者的经验和偏好,综合交战双方的角度、速度、高度、飞机性能、武器性能及攻击等因素,综合优势函数为各优势函数及偏好权向量的乘积。偏好权向量W的表达式为:

W=[W1,W2,W3,W4,W5,W6]

(7)

综合优势函数S为:

S=W1S1+W2S2+W3S3+W4S4+

W5S5+W6S6

(8)

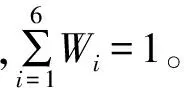
不同作战态势及作战阶段下各影响因素重要程度的变化,通过调整加权系数来体现。根据空战机动决策过程中的各影响因素的重要性,确定第i影响因素的权重为:

(9)

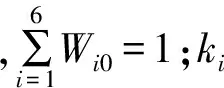
1.8 目标运动状态的预测

假设在当前时刻测定目标位置及运动状态已知,目标保持当前运动状态,根据式(1)预测下一决策时刻目标位置及运动状态,并根据目标位置及运动状态对优势函数进行预测,以备进行决策优化时使用。

2 自适应伪并行遗传算法

本文的并行遗传算法采用粗粒度模型(也称孤岛模型),其原理为将初始的种群分为若干个子种群,并将子种群分配到各子节点上单独进行遗传进化,每隔一定代数,将各子种群中的最优个体迁移到其它子种群中,并接纳其它子群体送来的最优个体[11]。实际应用时可以在一台计算机上串行实现粗粒度并行遗传算法,即伪并行遗传算法。虽然伪并行遗传算法不具有并行计算的速度优势,但仍具有避免“早熟”的性质,有效地降低了遗传算法在全局搜索能力方面固有的缺陷[12]。

算法流程如下:

(1)初始化。根据实际问题确定编码方式,并生成初始群体,编码方式有二进制编码和实数编码。

(2)设计适应度函数,计算每个个体的适应度值。

(3)选择操作。按照一定的规则从种群中分别选择一定数目的染色体进入下一代群体。本文采用多种选择方法,首先采用最佳个体保留策略,即将适应度值最高的个体不进行交叉和变异,直接选择进入下一代群体;其余的个体按照适应度值比例法,又称轮盘赌法[13]。

(4)交叉变异。将选择的染色体作为父代,根据交叉概率和变异概率,选择一定数目的染色体进行交叉和变异,得到下一代染色体。交叉概率Pc计算如下:

(10)

式中,Pc∈[Pc1,Pc2],Pc1,Pc2∈(0,1),一般情况下交叉概率Pc1,Pc2∈(0.3,0.9);fmax为群体中的最大适应度值;f′为要交叉的两个个体中较大的适应度值;favg为群体的平均适应度值。

变异概率Pm计算如下:

(11)

式中,Pm∈[Pm1,Pm2],Pm1,Pm2∈(0,1),一般情况下变异概率Pm1,Pm2∈(0.005,0.300);f为变异个体的适应度值。

(5)迁移。将适应度值高的个体根据规则发给其它子种群。本文采用自适应循环迁移算子,即根据子种群的相对适应度值调整迁移概率,将子种群中适应度高的个体发给其它子种群[14]。迁移概率Pq计算如下:

(12)

式中,k为比例系数,根据实际问题而定。

3 空战机动决策模型

3.1 飞机运动模型

飞机本身是一个弹性体,载荷的消耗和使用、操纵系统的运动和飞行员的移动使得质心位置随时变化,如果考虑这些因素,那么运动方程极为复杂,无法求解。本文假设飞机质量为常数,将飞机视为质点,在惯性坐标系中,用3个描述质心运动的运动学方程确定飞机的运动规律。

基于地理坐标系(北-天-东)建立运动学方程。假设飞机侧滑角和迎角均为0°,发动机安装角为0°,则飞机的运动学方程为:

(13)

(14)

式中,Vt为飞机速度;a为飞机加速度;θt为飞机航迹俯仰角;Δθ为飞机航迹俯仰角变化率;φt为飞机航迹偏转角;Δφ为飞机航迹偏转角变化率。

因a与当前飞行速度相关,根据飞机飞行规律可知:在最大速度时的加速度最大为0,在最小速度时的加速度最小为0。因此可以将加速度的取值范围表示为:

(15)

3.2 基于改进遗传算法的机动决策模型

首先将战斗机的飞行控制量离散化,组成染色体群体,每一个染色体代表一组控制量。其基本思想是n个染色体位数代表一个控制量,一条染色体可由多段控制量染色体组成。由3.1节可知,战斗机机动可总结为3个控制量进行控制,其中将控制量Δθ,Δφ及a的值域划分N=2n份,每一数值代表了3个控制量的大小,如表1所示。确定每个控制量对应的染色体位数n(向绝对值大的方向取整),则总的染色体位数为3n。其中,Δφ向右为正,Δθ向上为正,其编码控制方式如图1所示。

表1 编码方式

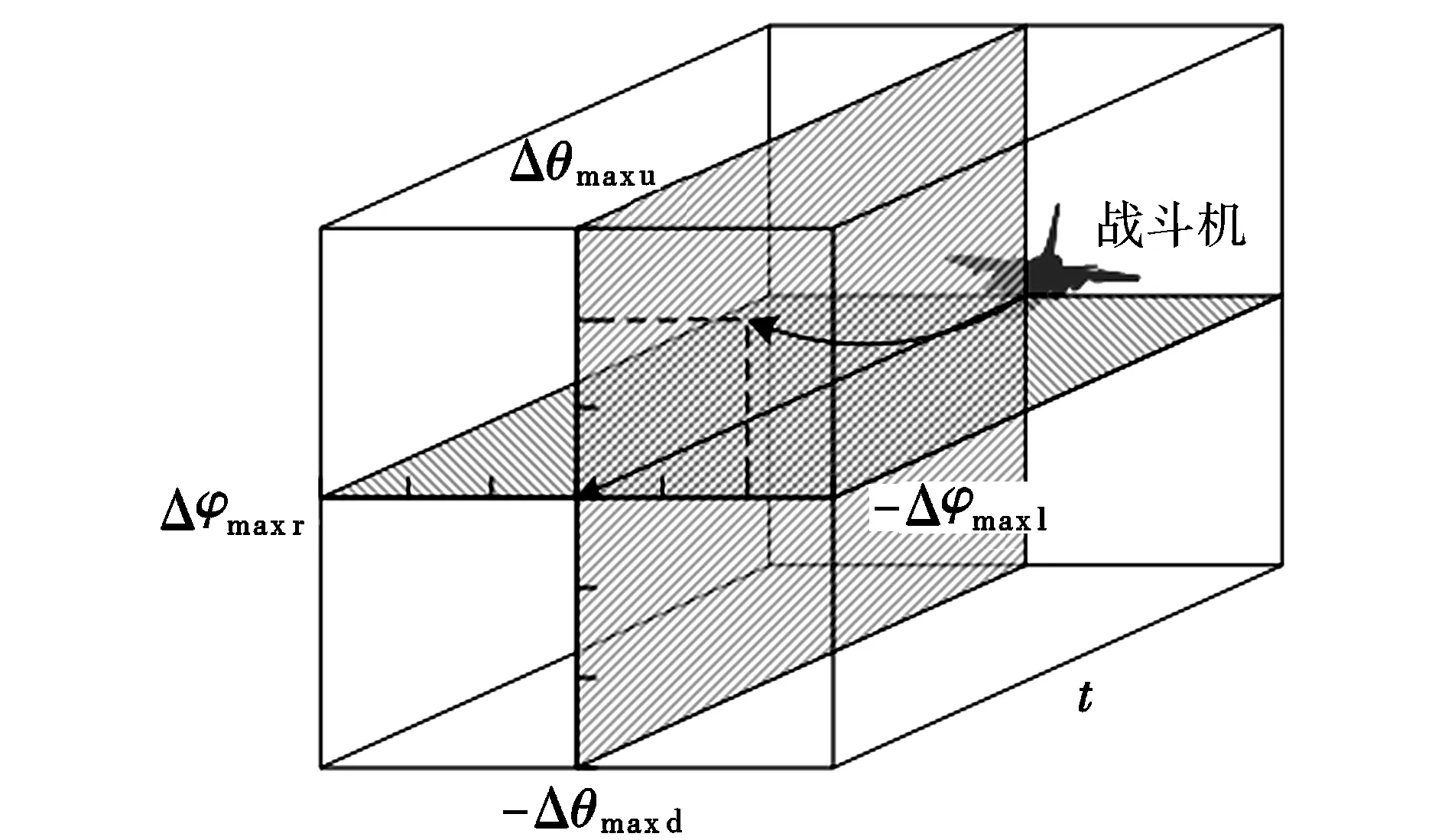
图1 飞机机动方式及编码示意图

由于控制量的值域范围不是相对0左右对称的,尤其是Δθ和a,因此本文假设其分别对其正负两部分进行N/2等分,具体计算公式如下:

(16)

Δφ和a的计算方式同上。那么任意一个染色体对应的控制量即可根据式(16)来计算得到。

在完成了控制量的离散化及编码之后,通过自适应伪并行遗传算法对染色体种群进行寻优。本文研究的目的是在空战中占据主动,增加我方的优势,因此选取我方的优势函数S为目标函数。

(17)

其余的遗传操作按照第2节的步骤进行。通过多次迭代后可得到最优结果,对应的染色体即为最优的染色体,通过式(16)可计算染色体对应的3个控制量值,即为此决策过程中最优的机动决策方案。经多次决策就可完成整个空战过程的机动决策。

4 仿真分析

仿真条件:假设敌我两架战斗机进行空战,我机初始坐标为(0,4,0) km,速度为300 m/s,初始航迹偏转角为0°,雷达反射面积SRCI为3 m2和0.1 m2,导弹最大射程为15 km,速度范围为200～400 m/s,雷达最大搜索方位角为60°,导弹最大发射角为45°;敌机初始坐标为(15.0,4.5,15.0) km,速度为250 m/s,初始航迹偏转角为180°,雷达反射面积为3 m2,导弹最大射程为10 km,敌机按照预定轨迹飞行;门限高度值为1 km;初始权重为(0.0,0.1,0.2,0.1,0.5,0.1),调整系数为(0.5,0.0,0.0,0.0,-0.5,0.0),每3 s进行一次机动决策。将初始群体分为两个子种群,每个子种群有20个染色体,每个群体进化50代,仿真结果如图2和图3所示。图2中,n为进化代数。

由图2可以看出,该算法的进化收敛速度很快。图2(a)和(b)分别在第一个子种群进化至19和20代时即已寻找到最优个体,因此两个子种群的自适应伪并行遗传算法可以保证机动决策的最优性。通过图3可以看出,SRCI=3 m2时,敌我隐身优势相当,在初始阶段,敌我双方距离较远时我机通过爬升机动占据有利位置,在10 s时达到最高高度4.948 km,随着敌我双方距离的缩短,角度优势函数权重变大,高度优势函数权重变小,因此我机逐渐转向角度瞄准;SRCI=0.1 m2时,我机隐身优势及攻击优势函数值较大,因此我机主要进行角度瞄准,以提前进入攻击位置。仿真结果验证了通过变权重自适应并行遗传算法计算得到的最优机动决策结果完全达到了机动决策的目的。

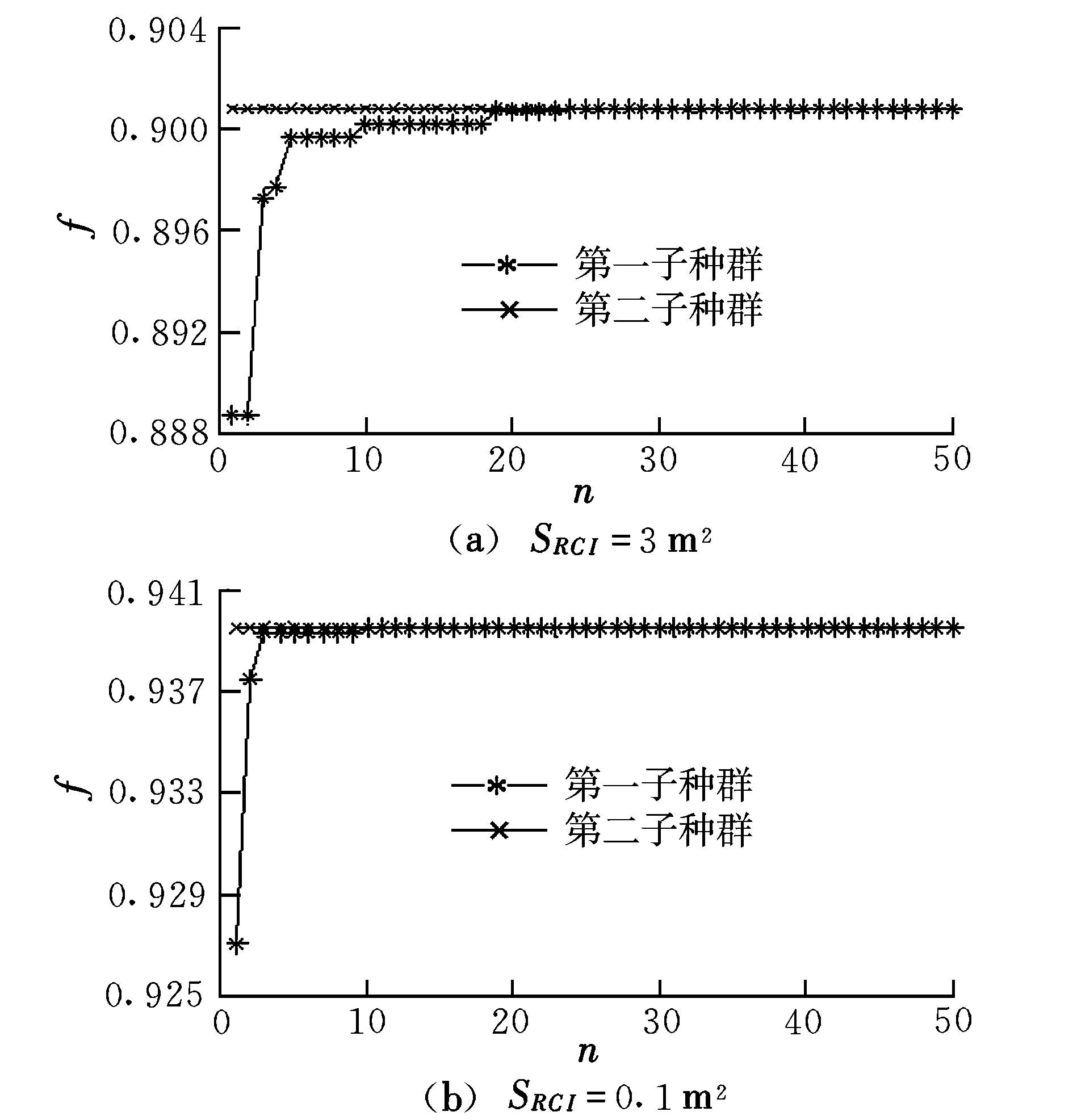
图2 最优个体适应度值与进化代数的关系

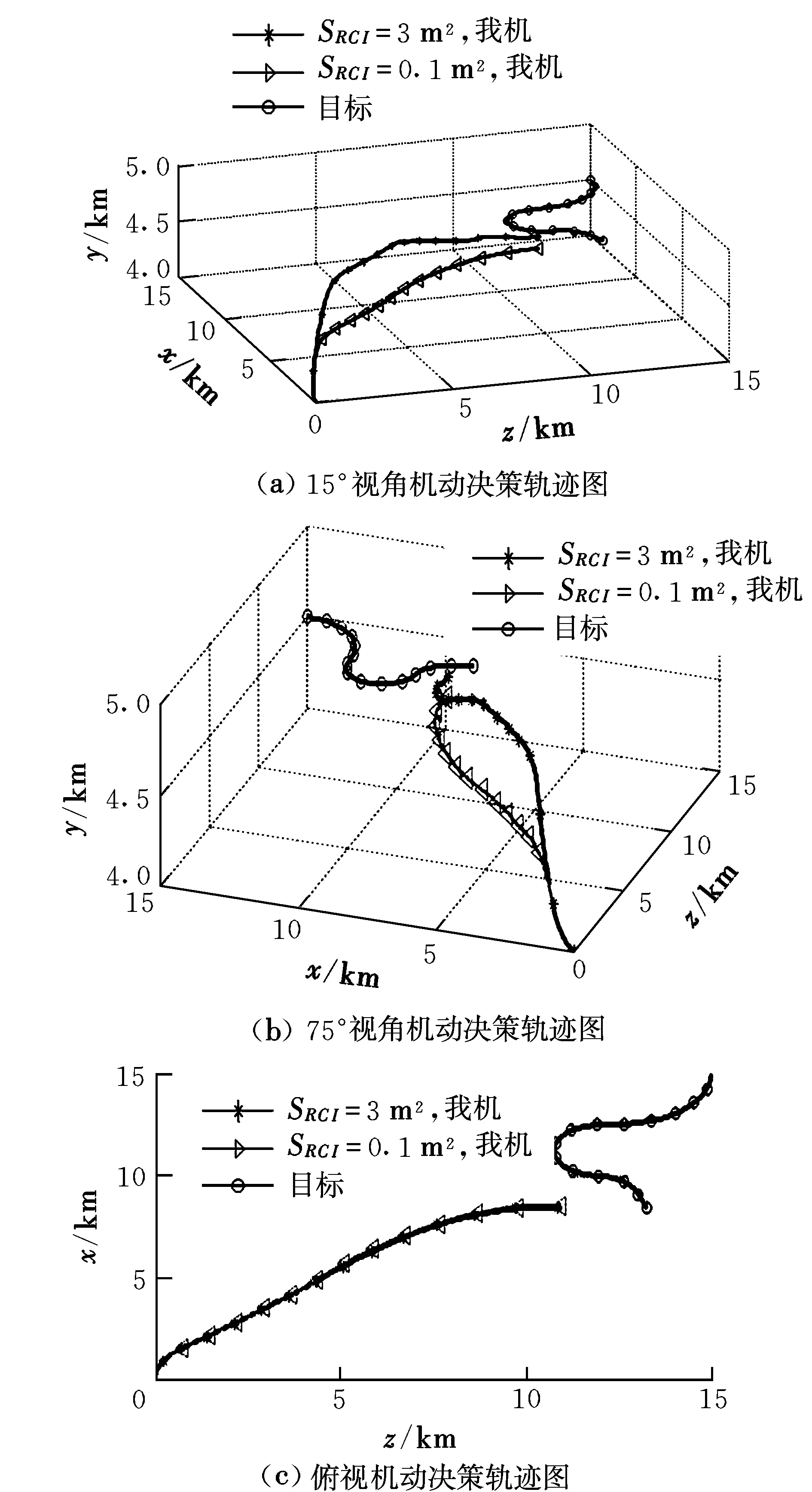
图3 机动决策轨迹图

5 结束语

本文对战斗机空战机动决策进行了研究,利用滚动时域控制思想,将机动决策问题阶段化,将控制量细化、离散化,并将变权重自适应并行遗传算法应用到机动决策中,重点分析了目标函数的建立、编码以及变权重的确定,并对理论进行了仿真验证。由仿真结果可以看出,变权重自适应并行遗传算法在空战机动决策方面是有效可行的,为空战机动决策研究提供了参考依据。

[1] James S,Jonathan P,Brian W,et al.Air-combat strategy using approximate dynamic programming[J].Journal of Guidance,Control,and Dynamics,2010,33(5):1641-1654.

[2] 周德云,李锋,蒲小勃,等.基于遗传算法的飞机战术飞行动作决策[J].西北工业大学学报,2002,20(2):109-112.

[3] 刘东坡.基于滚动机制的有限时域设备更新方法[D].济南:山东大学,2010.

[4] Benjamin R Carter.Time-optimization of high performance combat maneuvers [D].Monterey:Naval Postgraduate School,2005.

[5] 徐玮.一种基于复形调优遗传算法的多学科优化方法[J].系统工程与电子技术,2010,32(4):869-872.

[6] 张涵璐,吴振森,张昌民,等.BRDF的遗传算法和遗传模拟退火算法建模及比较[J].系统工程与电子技术,2010,32(7):1529-1531.

[7] 李正光,黄明,梁旭.改进伪并行遗传算法求解作业车间调度问题[J].数学的实践与认识,2010,40(1):133-138.

[8] 焦李成,尚荣华,马文萍,等.多目标优化免疫算法、理论和应用[M].北京:科学出版社,2010.

[9] 肖冰松,方洋旺,胡诗国,等.一种新的超视距空战威胁评估方法[J].系统工程与电子技术,2009,31(9):2162-2166.

[10] 郭昊,周德云,张堃.无人作战飞机空战自主机动决策研究[J].电光与控制,2010,18(8):28-32.

[11] 李培,郝晓光,周文.基于伪并行遗传算法的无源电力滤波器优化设计[J].电测与仪表,2011,48(7):75-81.

[12] 王萍萍,潘丰.基于改进伪并行遗传算法的函数优化[J].江南大学学报,2010,9(1):12-16.

[13] 元昌安,彭昱忠,覃晓, 等.基因表达式编程算法原理与应用[M].北京:科学出版社,2010.

[14] 陈勇,刘勇,鲍胜利.基于伪并行遗传算法的路径测试数据自动生成[J].四川大学学报,2009,41(5):141-145.

(编辑：姚妙慧)

Decision-makingforaircombatmaneuveringbasedonvariableweightpseudo-parallelgeneticalgorithm

ZHANG Tao1,2, YU Lei1, ZHOU Zhong-liang1, LI Fei1

(1.Engineering Institute, Air Force Engineering University, Xi’an 710038, China;2.94831 Unit of the PLA, Quzhou 324001, China)

Considering a scenario of air combat involving two opposed fighters, a decision-making model based on variable weight adaptive parallel genetic algorithm is established by the continually updated preponderance function. This paper mainly discusses the preponderance function, variable weight function, coding mode and operator. The experiment results demonstrated that this algorithm is feasible because it could complete the decision-making for air combat.

adaptive pseudo-parallel genetic algorithm;variable weight;decision-making for maneuvering;preponderance function

E844

A

1002-0853(2012)05-0470-05

2011-12-26;

2012-04-24

航空科学基金资助(20095196012)；校博士生创新基金资助(Dx2010106)

张涛(1982-)，男，山东新泰人，博士研究生，主要研究方向为航空武器系统总体、仿真与控制。