Simulink中倾转旋翼机飞行力学模型研究
2012-11-06沙虹伟
沙 虹 伟
(南京航空航天大学 直升机旋翼动力学国家重点实验室, 江苏 南京 210016)
Simulink中倾转旋翼机飞行力学模型研究
沙 虹 伟
(南京航空航天大学 直升机旋翼动力学国家重点实验室, 江苏 南京 210016)
在Simulink环境中建立了功能健全的倾转旋翼飞行力学模型。该模型包含了旋翼、机翼、机身、尾翼等部件气动力模块与操纵机构模块,其中旋翼气动力的计算采取了准定常叶素理论和均匀入流假设,而机翼、机身、尾翼等部件气动力的计算则采用了升力线理论,并考虑了旋翼尾流的影响。最后,以XV-15为样机进行了配平和特征根的计算,并将计算结果与GTRS模型结果进行了对比,验证了该建模方法的有效性。
倾转旋翼机; 飞行力学模型; 仿真; Simulink
引言
倾转旋翼机有多种飞行模式,飞行包线宽,具有很大的开发潜力,但也包含了很多技术问题[1-2],其中又以建立倾转旋翼机飞行力学模型尤为突出。健全的飞行力学模型一般具备模型配平、线性模型提取和响应计算三方面的功能。采用常规建模方法虽然可以使飞行力学模型具备以上功能,但研究人员需要研究相应的算法,额外编写大量的计算代码,这不仅增加了研究人员的工作负荷,而且增加了程序出错的概率。另外,研究人员在编程水平以及编程风格方面参差不齐,使得完成的程序在可读性、继承性和模块化方面水平不高,这也制约了倾转旋翼机飞行力学模型的发展,而在Simulink中建立倾转旋翼机飞行力学模型不仅能实现模型配平、线性模型提取及响应计算等功能,而且还可以方便地对各模块进行升级,可以轻松地解决以上问题。在Simulink集成建模环境中,研究人员只需拖拽不同的模块,书写很简短的代码即可获得功能健全、模块化程度高的模型。因此,本文在研究了各部件气动力特点及操作机构特点的基础上,在Simulink环境中建立了全量非线性倾转旋翼机飞行力学模型,并以XV-15为样机进行了配平和特征根计算,将所得结果与文献[3]提供的GTRS模型结果进行了对比,验证了本文提出的建模方法的有效性。
1 飞行力学数学模型
在Simulink中建立倾转旋翼飞行力学模型前,需先建立倾转旋翼机飞行力学数学模型,该数学模型包含了右(左)旋翼、机身、机翼、右 (左)短舱及尾翼等部件的气动力数学模型及操纵机构数学模型。
1.1 旋翼气动力数学模型
在建立旋翼气动力数学模型时采用了以下假设:桨叶刚性、扭转角线性分布且为铰接式、静态均匀入流、桨叶挥舞运动简化至一阶谐波量[4-5]。以右旋翼为例,其求解过程如下:
(1)计算旋翼桨毂中心的气流速度。设短舱旋转支点O处气流为[u,v,w]O,机体角速度为[p,q,r],短舱倾角为i(90°为直升机模式),桨榖中心到O点的距离为L,则旋翼桨榖中心气流速度为:
式中,下标W代表桨毂风轴系。
(2)计算旋翼诱导速度。由动量理论得到的旋翼诱导速度见下式,该式采用数值方法求解。
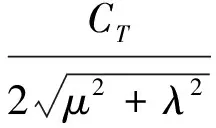
vi=(λ0-λ)ΩR
(4)计算旋翼气动力及气动力矩,并转换到机体轴系中。假设右旋翼气动力描述为:
[HW,SW,TW,LW,MW,QW]r=
f(uW,vW,wW,pW,qW,rW,AW,BW,…)r
式中,AW和BW分别为风轴系下旋翼的横、纵向周期变距;下标r表示右旋翼系统。左旋翼气动力可由对称原理获得。
1.2 机翼气动力数学模型
受旋翼尾流影响,机翼上存在受旋翼尾流影响的滑流区和不受旋翼尾流影响的自由区。机翼气动力由这两部分气动力相加所得。本文采用经验公式确定滑流区机翼的面积Swss[6](下标w和ss分别代表机翼和滑流区)。设机翼滑流区气动压力中心为(x,y,z)w,机体质心线速度为[u,v,w],则滑流区机翼气动压力中心点处来流速度为:
式中,η为诱导速度影响系数,1≤η≤2。
则滑流区机翼升阻力等参数如下:
Lwss=qwssSwssCLwss
Dwss=qwssSwssCDwss
CLwss=α(αwss-α0)+(∂CLwss/∂δail)δail
αwss=arctan(wwss/uwss)
式中,α0,∂CLwss/∂δail和δail分别为机翼零升迎角、机翼升力增量对副翼偏转量的导数和副翼偏转量。
倾转旋翼机在低速飞行时,旋翼尾流使得机翼处于大迎角状态,因而在建立机翼气动力模型时需要注意这一点。自由区机翼气动力只需在以上过程中设定η=0即可获得。
1.3 机身气动力数学模型
本文采用经验公式确定机身气动力。设机身压力中心为(x,y,z)f,来流速度为[u,v,w]f,下标f表示机身,则机身气动力及力矩为:
式中,CDf,CLf,CSf,CMxf,CMyf和CMzf分别为机身3个方向的气动力及力矩系数,它们是机身迎角和侧滑角的函数;Af和Lf分别为机身特征面积和特征长度。
短舱气动力模型与机身气动力模型相似,只需把短舱等效为平板来处理,本文不再重复。
1.4 尾翼气动力数学模型
设平尾气动压力中心为(x,y,z)e,下标e表示平尾,则平尾气动压力中心处的来流速度为:
则平尾气动力等参数为:
Le=qeSeCLe
De=qeSeCDe
CLe=ααe+(∂CLe/∂δelev)δelev
αe=arctan(we/ue)
式中,∂CLe/∂δelev和δelev分别为平尾升力增量对升降舵偏转量的导数和升降舵偏转量。垂尾气动力处理方法与上述过程相似。
1.5 操纵机构模型
倾转旋翼机与一般飞行器相比,具有更多的气动操纵面,对应的控制量也较多,有如下9个:左/右旋翼总距θ0l/θ0r、左/右旋翼纵/横向周期变距Al/Ar和Bl/Br、副翼偏转δail、升降舵偏转δelev及方向舵偏转δrud;而驾驶员的操纵量一般只有如下4个:总距杆位移δcoll、操纵杆纵向位移δlong、操纵杆横向位移δlat及脚蹬位移δped。合理设计4个操纵量与9个控制量之间的传动关系是倾转旋翼机操纵机构需要解决的难点。本文所建操纵机构模型如下[7]:
θ0l=-δcoll·θ0l/δcoll-(δlat-δlat,neu)·θ0l/δlat
θ0r=-δcoll·θ0r/δcoll+(δlat-δlat,neu)·θ0r/δlat
Bl=-(δlong-δlong,neu)·Bl/δlong+
(δped-δped,neu)·θ0l/δped
Br=-(δlong-δlong,neu)·Br/δlong-
(δped-δped,neu)·θ0r/δped
Al=Ar=0
δelev=(δlong-δlong,neu)·δelev/δlong
δail=-(δlat-δlat,neu)·δail/δlat
δrud=(δped-δped,neu)·δrud/δped
式中,带有neu下标的变量表示驾驶杆位于中立位置时对应的操纵量;()/δ()表示单位操纵量的改变引发的相应控制量的改变量,体现了操纵机构的传动关系。由上式可发现,本文建立的操纵机构模型使倾转旋翼机旋翼纵向周期变距与升降舵偏转、旋翼总距与副翼偏转、旋翼纵向周期变距与方向舵偏转之间存有联动关系。
1.6 数学模型
将以上各气动部件输出的气动力输入至六自由度机体动力学方程,再补充运动方程即可组成完整的飞行力学数学模型。
2 仿真模型的建立
首先根据上节内容在Simulink中分别建立了各部件的气动模块、输入/输出模块和运动方程环节,然后根据它们之间的逻辑关系,用信号线连接起来[4],由此得到了倾转旋翼机的飞行力学模型,如图1所示。
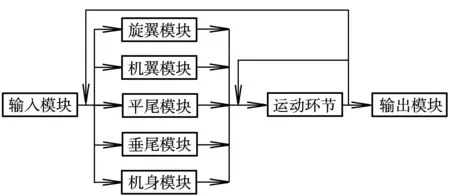
图1 倾转旋翼机飞行力学仿真模型原理框图
3 算例验证
上节中得到的飞行力学仿真模型具有模型配平、配平点处线性模型提取以及响应计算三个功能。很明显,该模型能实现响应计算。对于该模型具备的配平计算和线性模型提取功能,本文以XV-15为样机展开说明,同时将计算结果与文献[3]提供的GTRS模型的计算结果进行了比较,以验证本文所建建模是否合理有效。
对于在Simulink中建立的模型,系统提供了trim函数来获得模型不同要求时的配平状态量,对该函数本文不作解释,直接给出了倾转旋翼机飞行力学模型在直升机和飞机模式时不同水平前飞速度情况下的操作及状态量配平结果,如图2~图9所示。

图2 直升机模式总矩配平结果

图3 直升机模式俯仰角配平结果
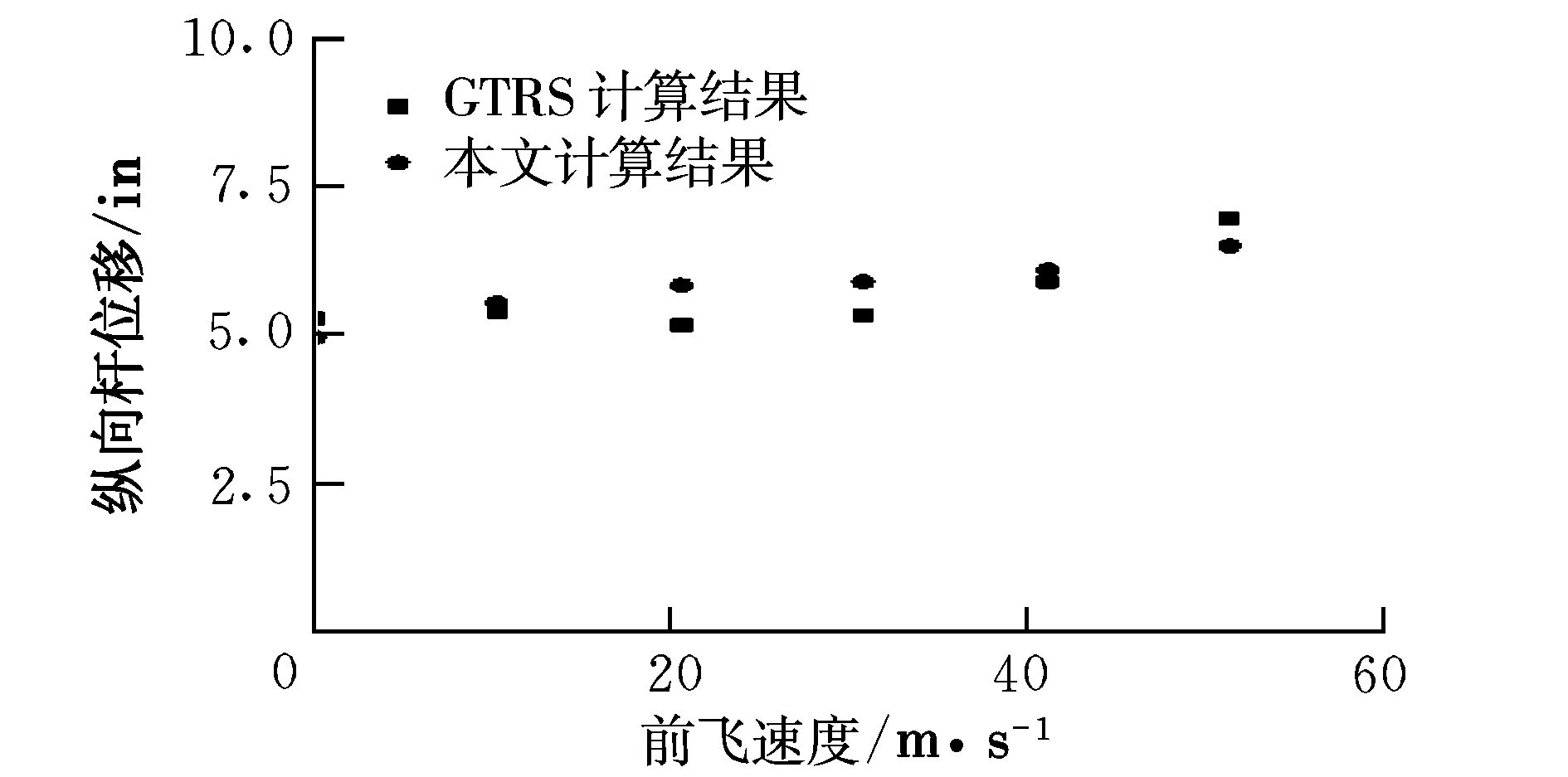
图4 直升机模式纵向杆位移配平结果
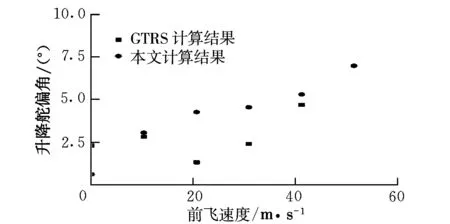
图5 直升机模式升降舵偏角配平结果
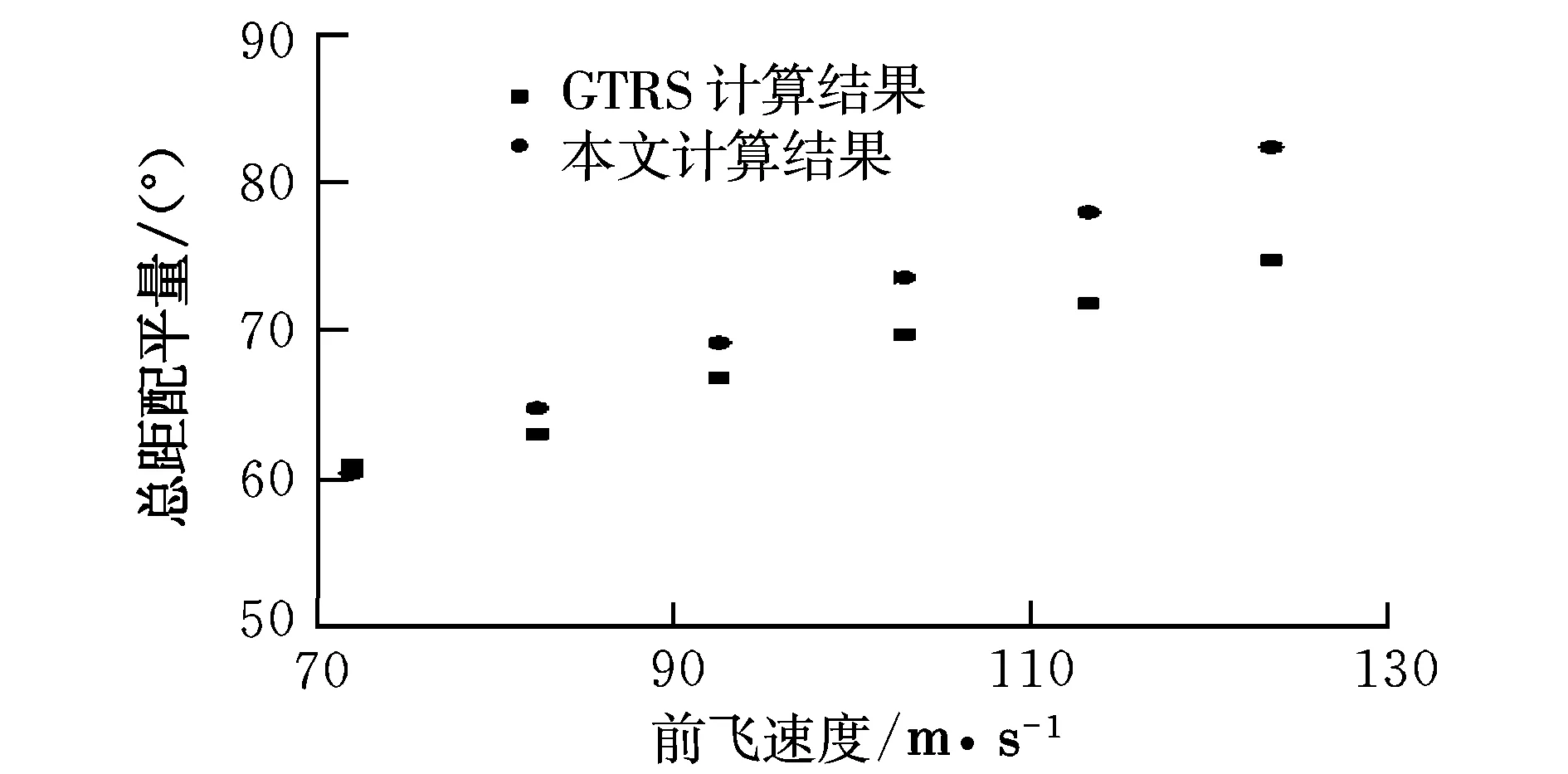
图6 飞机模式总矩配平结果

图7 飞机模式俯仰角配平结果

图8 飞机模式纵向杆位移配平结果

图9 飞机模式升降舵偏角配平结果
由图2~图9可发现,两组结果除了在飞机模式前飞时升降舵偏角存在差异外,其它操纵量及状态配平结果都极为吻合。进一步的分析表明,这两组结果之间的差异很可能是模型间机身和机翼俯仰力矩的差异造成的,但由于缺少GTRS的具体建模资料,很难做出深入比较,不过整体上这两组结果还是极为吻合的,表明了本文模型的准确性。
得到配平状态后,利用系统提供的Linmod函数可以很方便地得到平衡点处的线性模型,结果如下:
计算状态A阵,可得到21个特征根。分析其特征向量,可选出对应于机身运动的9个特征根,略去其中对应航向运动的0特征根,其余8个根的分布见图10和图11,图中还给出了GTRS计算结果。由图可知,两者更是趋向吻合,这也证实了本文所建立的倾转旋翼机飞行力学模型是合理和准确的。

图10 直升机模式悬停时的系统特征根

图11 飞机模式前飞速度为102 m/s时的系统特征根
4 结束语
在Simulink中建立倾转旋翼机飞行力学模型是一种高效的途径,由此获得的飞行力学模型功能健全,模块化程度高,扩充性和移植性很高,而且很便于倾转旋翼机飞控系统的研究。文中建立的倾转旋翼机飞行力学仿真模型的阶数高,且合理准确,较好地反映出了倾转旋翼机的飞行力学特性,可用于分析各参数对其动稳定性以及飞行品质等方面影响的研究。由于利用系统提供的Linmod函数可直接得到模型平衡点处的线性模型,因此本模型不适宜分析各部件参数对倾转旋翼机静稳定性的影响,但可对其动稳定性进行分析。
[1] Harendra P B,Joglekar M J,Gaffey T M,et al.A mathematical model for real time flight simulation of the Bell Model 301 tilt rotor research aircraft [R].NASA-CR-114614,1973.
[2] 沙虹伟.无人倾转旋翼机飞行力学建模与姿态控制技术研究[D].南京:南京航空航天大学,2007.
[3] Kristi M K.Stability and control modeling of tilt-rotor aircraft[D].Maryland:University of Maryland,2007.
[4] Chen R T N.Effects of primary rotor parameters on flapping dynamics[R].NASA TM-431,1980.
[5] Chen R T N.A simplified rotor system mathematical model for piloted flight dynamics simulation[R].NASA TM-78575,1973.
[6] Carlson E B,Zhao Yiyuan,Robert T N.Optimal tiltrotor runway operations in one engine inoperative[R].AIAA-99-3961,1999.
[7] 宋彦国,王焕瑾,沙虹伟,等.倾转旋翼飞行器飞行力学模型研究[J].空气动力学学报,2008,26(2):192-196.
(编辑:姚妙慧)
ResearchonflightdynamicsoftiltrotoraircraftbaseonSimulink
SHA Hong-wei
(National Key Laboratory of Rotorcraft Aeromechanics, NUAA, Nanjing 210016, China)
A flight dynamics Simulink model of the tilt rotor aircraft was established in Simulink after the research into the aerodynamic of the rotors, wing, fuselage, nacelle, and empennage and control system. Quasi-steady element theory was used to analyze the lift, drag, moment and the flapping motion of the rotors. The lift line theory was used to research the aerodynamics of others with the rotor wake considered, and then the XV-15 tilt rotor aircraft is used as a sample aircraft for trimming and calculating of characteristic root. The results are compared to those of GTRS model, which show effectiveness of the modeling method, so the model could be helpful to realize the characteristics of tilt rotor aircraft, also useful to flight control design.
tilt rotor aircraft; flight dynamics model; simulation; Simulink
V212.4
A
1002-0853(2012)05-0389-04
2011-12-07;
2012-04-25
沙虹伟(1982-),男,江苏泰州人,博士研究生,主要研究方向为直升机飞行力学。
