高空太阳能无人机飞行动力学建模与分析

肖伟, 周洲, 祝小平, 王睿

(1.西北工业大学 无人机特种技术国家重点实验室, 陕西 西安 710065;2.西北工业大学 无人机研究所, 陕西 西安 710072)

高空太阳能无人机飞行动力学建模与分析

肖伟1, 周洲1, 祝小平2, 王睿1

(1.西北工业大学 无人机特种技术国家重点实验室, 陕西 西安 710065;2.西北工业大学 无人机研究所, 陕西 西安 710072)

高空长航时太阳能无人机的机翼是超柔性结构,在飞行中气动弹性变形体现了几何非线性特征,并与飞行动力学响应耦合,从而改变无人机的飞行特性。基于哈密顿原理,对柔性无人机进行了动力学建模,计算了不同装载时无人机的配平状态,并对飞行动力学特性进行了分析。结果表明,由于弹性变形和集中载荷的影响,无人机的短周期频率减小且阻尼增大,长周期运动与结构变形运动发生耦合,导致长周期的阻尼减小。

太阳能无人机; 气动弹性; 几何非线性; 飞行动力学

引言

太阳能无人机以太阳能为动力,不受常规动力飞机机载能源有限的约束,适合执行超长时间的侦察、监视和通信中继等任务,是高空长航时无人机的一个重要发展方向[1]。

高空长航时太阳能无人机的机翼展弦比很大、结构面密度很小,飞行中结构变形明显且特征频率低,容易与飞行动力学响应耦合,从而改变无人机的动力学响应特性。在飞行动力学建模时需要考虑机翼弹性变形的影响[2-3]。

本文基于哈密顿原理,在机翼的局部坐标系下推导了无人机的飞行动力学方程,并将其应用于太阳能无人机的动力学特性的分析。

1 无人机的动力学方程

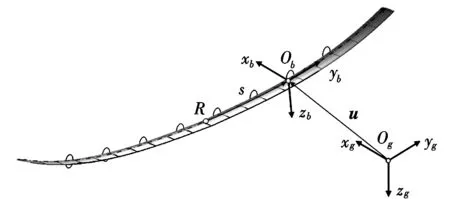
图1 高空太阳能无人机及其坐标系示意图

机翼运动速度v和角速度ω在局部坐标系中定义,由地轴系到机翼局部坐标系的转换矩阵为Cbe,由局部坐标系欧拉角的变化率到角速度ω的转换矩阵为Cd。以上各量均是时间t和曲线坐标s的函数,文中用上标(·)表示物理量对时间的导数,右标(′) 表示对曲线坐标s的导数。

机翼局部坐标系的运动学方程[4]为:

(1)

(2)

图2为机翼局部坐标系下的运动关系示意图。

图2 机翼局部坐标系下的运动关系示意图

假设机翼截面为刚性,设ξ为质心在局部坐标系内的位置向量,由图2中的几何关系可知,该截面质心处的速度为:

vcg=v+ω×ξ

(3)

于是,由质点系动能的合成定理,可以将机翼的动能表示为:

(4)

式中,μ为单位长度翼段的质量;Icg为其相对质心的惯量矩阵。将式(4)对速度、加速度求偏导,可以得到机翼动能变分的表达式为:

(5)

式中,p,h分别为局部坐标系的广义动量和广义角动量。由式(3)和式(4),并应用转动惯量张量的平行轴定理,可以得到:

p=μv+μξ×ω

(6)

h=μξ×v+Iω

(7)

式中,I为单位长度翼段相对机翼局部坐标系原点的惯量矩阵。式(5)中的速度和角速度的变分可由一般坐标系运动学方程在局部坐标系内得到:

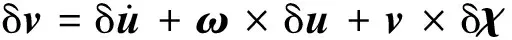
(8)

(9)

由太阳能无人机大展弦比和低翼载的特点可知,在飞行中机翼整体变形明显,但在机翼局部变形不大。采用Hoges梁假设,设机翼变形前曲率为0,机翼局部的应变γ和κ分别可以表示为[5]:

(10)

(11)

式中,e为局部坐标系yb轴方向的单位向量。由材料力学原理可知,机翼局部的应力fe、力矩Me与应变γ和κ的关系为:

(12)

式中,K为结构刚度矩阵。于是,机翼弹性势能的变分可以表示为:

(13)

根据式(10)和式(11),类似于速度和角速度,应变的变分也可以在局部坐标系内得到:

(14)

(15)

将机翼的非保守力fr、力矩Mr定义在机翼局部坐标系,则有总外力的虚功:

(16)

综上,由式(5)、式(13)及式(16),根据哈密顿原理:

(17)

得到:

(frδu+Mrδχ)]dsdt=0

(18)

积分上式,并由欧拉-拉格朗日方程,得到机翼动力学方程为:

(19)

Me′+κ×Me+(e+γ)×fr+Mr=

(20)

2 气动力、推力和重力模型

上文推导的方程中非保守力包括重力、气动力和推力。为了建立无人机的飞行动力学方程,需要对以上各力建模。

太阳能无人机的展弦比很大,本文应用片条理论,认为机翼的弦向剖面上的气动力按照二元机翼理论计算。作弹性运动时机翼所受的气动力随时间变化,应用格罗斯曼准定常假设[6],得到二维翼型上的准定常气动力系数为:

(21)

(22)

由此可以计算气动力fa和力矩Ma。忽略受扰动过程中螺旋桨的转速变化,则推力随来流速度变化的系数为:

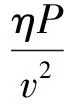
(23)

式中,η和P分别为螺旋桨的效率和轴功率。由此可以计算推进力fT和力矩MT。

单位长度机翼的重力在地面坐标系定义为:

(24)

对应于式(19)和式(20),上述各力、力矩均在机翼局部翼段上考虑,因而它们同样是时间t和曲线坐标s的函数。将上述各力、力矩转换到机翼局部坐标系内有:

(25)

Mr=Ma+ξ×(CbefgG)+MT

(26)

3 方程的线性化

结合气动力、推力和重力的表达式,将式(19)和式(20)与式(1)和式(2)联立,可以得到表示太阳能无人机的状态方程组。为了便于进行动力学分析,以下对状态方程进行时域内展开和线性化处理。将机翼分为n段,则状态量为3×4×n维列向量:

[x1,x2,x3,x4]T=[v,ω,u,χ]T

(27)

将式(19)和式(20)泰勒展开,保留一次项,可得无人机运动的小扰动方程为:

(28)

其中:

(29)

由运动学关系式(1)和式(2)小扰动线性化得到:

(30)

为了保证求偏导数的连续性,本文中将运动量v,ω等在局部翼段内定义,将内力fe、内力矩Me和应变γ,κ在相邻两翼段中间节点定义,利用以下关系实现状态量的求偏导和求平均运算:

(31)

(32)

式中,d为分段后小段机翼的长度;xi,j为对应第j段机翼的状态量xi。

同时,将配平状态下基准量的叉乘运算改写成线性矩阵点乘的形式,如:

κ0×Δfe=Cκ0Δfe

(33)

则根据式(1)、式(2)、式(19)及式(20),由求导运算、求平均运算、叉乘矩阵变换可以计算得到A1～A4,进而得到无人机的小扰动特征方程。

4 无人机飞行动力学特性分析

4.1 配平计算

图3 不同载荷下无人机机翼中点的配平迎角

机翼静气动弹性变形随集中载荷的变化如图4所示。

图4 不同载荷下无人机配平状态的静变形

4.2 动态特性计算

在按上述方法求解静变形计算的基础上,在平衡点对状态方程线性化,求解特征根,从而研究太阳能无人机的基本动态特性。结果显示,随着无人机载荷的增加,无人机上弯变得明显,这个静变形效应使得无人机的纵向短周期运动模态的阻尼增大,直至收敛,其特征根变化趋势如图5所示。

图5 载荷增加时无人机纵向特征根轨迹(短周期)

由于载荷集中在无人机的中部,使得无人机的长周期运动与机翼的低频弹性模态发生耦合,从而使得无人机纵向长周期运动的阻尼减小,其特征根变化趋势如图6所示。由图6可知,随着集中载荷重量的增加,系统的特征根由负实部变为正实部,无人机长周期与结构耦合模态有发散的趋势。

图7显示了长周期运动过程中无人机的变形情况。当考虑机翼弹性的影响时,太阳能无人机的长周期模态与结构模态出现耦合,其间不仅存在动能与重力势能的转换,同时还包括了动能与弹性势能的相互转换,结果导致长周期模态稳定性降低。

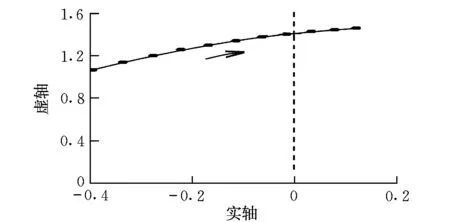
图6 载荷增加时无人机纵向特征根轨迹(长周期)

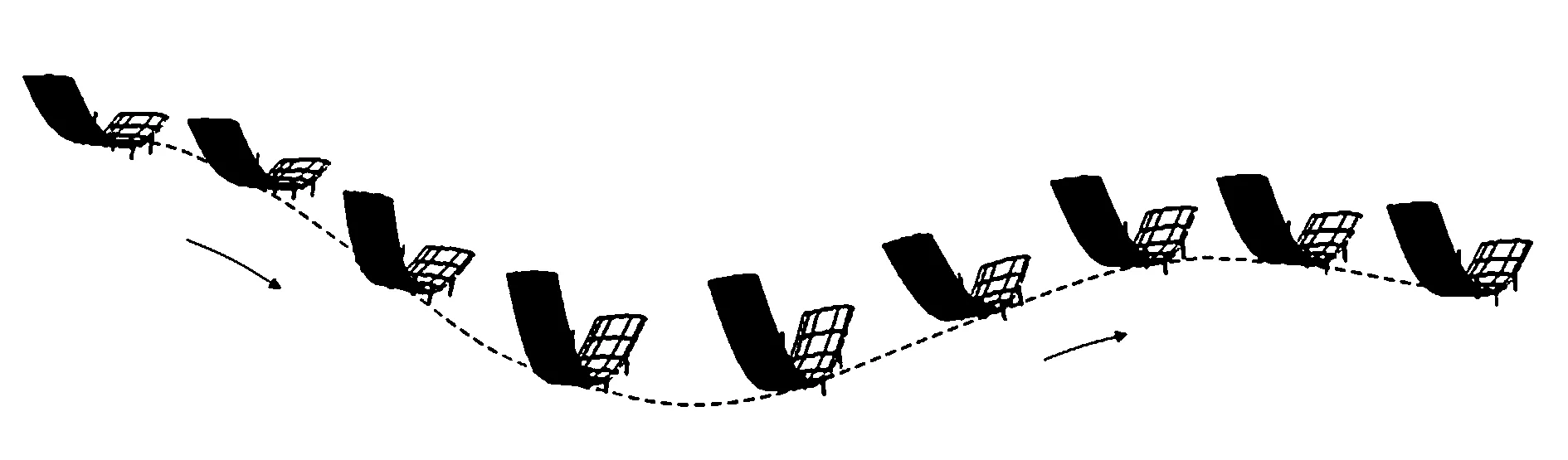
图7 无人机长周期与结构耦合模态

5 结论

通过本文的研究可得到以下结论:

(1)基于哈密顿原理和梁结构模型,推导了超柔性太阳能无人机的动力学方程。研究发现,在挂载集中载荷时,超柔性无人机配平状态存在较大变形,弹性变形对飞行性能和飞行品质有明显的影响。

(2)由于静态弹性变形,使得无人机的短周期阻尼减小,变形量增加时短周期特征根最终收敛为实根。

(3)在集中载荷的情况下,气动弹性变形导致机翼结构变形和无人机的长周期运动耦合严重,导致阻尼减小,可能使得长周期与结构耦合模态不稳定,影响飞行安全。

[1] 高广林,李占科,宋笔锋,等.太阳能无人机关键技术分析[J].飞行力学,2010,28(1):1-4.

[2] Giulio Romeo,Giacomo Frulla.Heliplat:aerodynamic and structural analysis of HAVE solar powered platform [R].AIAA 2002-3504,2002.

[3] Mayuresh J Patil.Nonlinear aeroelastic analysis,flight dynamics,and control of a complete aircraft [D].Atalnta:Ph.D.Dissertation,Georgia Institute of Technology,GA,May,1999.

[4] 方振平,陈万春,张曙光.航空飞行器飞行动力学[M].北京:北京航空航天大学出版社,2005.

[5] Dewey H Hodges.Geometrically exact,intrinsic theory for dynamics of curved and twisted anisotropic beams [J].AIAA Journal,2003,41 (6):1131-1137.

[6] 陈桂彬,邹丛青,杨超.气动弹性设计基础[M].北京:北京航空航天大学出版社,2004.

(编辑：姚妙慧)

ModellingandanalysisonflightdynamicsofhighaltitudesolarUAV

XIAO Wei1, ZHOU Zhou1, ZHU Xiao-ping2, WANG Rui1

(1.National Key Laboratory of Science and Technology on UAV, NWPU, Xi’an 710065, China;2.UAV Research Institute, NWPU, Xi’an 710072, China)

High altitude long endurance (HALE) solar powered UAV is highly flexible in flight, the aircraft motion is coupled with geometrically nonlinear structural deformation. This paper establishes mathematical model for the flexible UAV with large deformation based on Hamilton priciple, it can be used for analysis of triming of the UAV and flight dynamics analysis about the trimmed-state. Results are generated for a typical high-aspect-ratio solar UAV, on account of flexibility, the pair of complex short-period roots merges to become real roots, and the phugoid mode goes unstable.

solar UAV; aeroelasticity; geometrically nonlinear; flight dynamics

V212.1; V279

A

1002-0853(2012)05-0385-04

2011-01-16;

2011-05-23

国防基础科研基金资助(A2720060290)

肖伟(1982-),男,湖南湘潭人,博士研究生,主要研究方向为飞行动力学与控制。