基于希尔伯特—黄变换的径流规律分析

骞 浩,赵 毅,徐 波,郑俊耀

(1.邯郸市水利局 漳滏河灌溉供水管理处,河北 邯郸 005600; 2.华北水利水电学院 数学与信息科学学院,郑州 450011)

2012-08-20

骞浩(1980—)，男，河北邯郸人，邯郸水利局漳滏河灌溉供水管理处助理工程师，研究方向为水资源管理。

基于希尔伯特—黄变换的径流规律分析

骞 浩1,赵 毅2,徐 波2,郑俊耀2

(1.邯郸市水利局 漳滏河灌溉供水管理处,河北 邯郸 005600; 2.华北水利水电学院 数学与信息科学学院,郑州 450011)

希尔伯特-黄变换在处理非线性、非平稳、弱相依、高度复杂的时间序列时，比传统的时间序列分析方法更具优势。通过对时间序列进行经验模态分解(EMD)，得到若干反映时间序列演化过程的本征模态函数(IMF)和序列变化的残余项(趋势项)，然后对每个本征模态函数作希尔伯特-黄变换，得到反映径流规律的统计特征值，从而获得序列变化的周期。对渭河临潼水文站的年径流观测数据进行分析，得出年径流变化存在9.52年、13.70年、21.74年和41.67年的周期，且有逐渐减小的趋势。

经验模态分解；径流规律；临潼水文站

1.引言

河川径流演变极其复杂，其演变过程受到诸多因素的共同作用，且影响因素随环境的不断变化而改变，所以河川径流序列是非线性、非平稳的。[1，2]因此研究该种径流序列需要寻找非线性、非平稳的方法。

1998年,学者Huang[3]等提出一种新的时间序列分析方法：希尔伯特-黄(Hilbert-Huang Transform，HHT)变换[4]。HHT包括经验模态分解(Empirical Mode Decomposition，EMD)和Hilbert变换两部分。EMD[5]是依据数据自身的时间尺度特征来进行信号分解，得到有限个反映时间序列[6]演化过程的本征模态函数(Intrinsic Mode Function，IMF)和序列变化的趋势项，再把IMF分量进行Hilbert变换，得到IMF随时间变化的振幅和频率，由频率求得相应周期。HHT具有以下优点：与傅里叶变换相比，HHT能分析非线性非平稳信号。小波变换在本质上是具有柔性时频窗的傅里叶变换，同样面临着傅里叶变换的局限性，而且小波基的多样性带来了如何有效选取小波基问题；HHT具有完全自适应性，能够自适应产生“基”，HHT不受Heisenberg测不准原理制约——适合不规则震动信号,传统方法受到Heisenberg测不准原理制约，即时间窗口与频率窗口的乘积为一个常数，这就意味着如果要提高时间精度就得牺牲频率精度。在处理非线性、非平稳的复杂信号时运用Hilbert-Huang变换，保留数据样本本身特性，结果能够反映出真实的物理过程。

本文在经验模态分解方法的基础上，运用Hilbert-Huang变换对渭河临潼站年径流水文序列趋势演变及周期进行研究分析。

2.HHT方法

2.1 经验模态分解(EMD)

EMD的特点就是把非线性非平稳的序列分解为多个IMF分量，并且在分解过程中能够保持自身的特性，其分解生成的分量具有完备性、正交性。每一个IMF必须满足两个条件：

(1)极大值、极小值和过零点的数目相等或者至多相差一个；

(2)在任意时刻由极大值确定的上包络和极小值确定的下包络的和为零。

这两个条件是EMD分解过程结束的收敛原则。通过EMD分解，任何复杂的信号都可以用有限个IMF之和表示。分解步骤如下：

(1)找出原始时间序列x(t)的所有局部极大值、极小值，运用三次样条函数进行插值，得到x(t)的上包络序列u(t)、下包络序列v(t)。

(2)对u(t)和v(t)取平均，即m(t),记m(t)=[u(t)+v(t)]/2。

(3)设h1(t)=x(t)-m(t)，检验h1(t)是否满足IMF的两个条件。对于不同的数据序列。如果满足以上条件，则h1(t)就是本征模态函数。否则，重复(1)～(2)，直至得到hk(t)满足IMF的两个条件，此时h1(t)就是第一个c1(t)；在求得第一个本征模态函数后，用原序列减去c1(t)，得到剩余值序列c1(t)，记r1(t)=x(t)-c1(t)。

(4)把r1(t)作为一个新的原始序列，重复(1)～(3)，直至剩余部分为一单调序列即残余项，分解结束。

通常情况下，IMF的停止依据为前后两个h(t)的标准差SD，即

(1)

经验证，当SD=0.2～0.3时IMF的稳定性比较好，并能够使IMF有清晰的物理意义。

2.2 Hilbert变换

原序列x(t)通过经验模态分解后，可分别对每个内在模函数做Hilbert变换，求得瞬时频率的Hilbert谱。将所有的本征模态函数Hilbert汇总，得到原序列x(t)的Hilbert谱。

对分解出的所有IMF进行Hilbert变换，ci(t)的Hilbert定义如下：

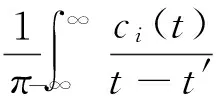
(2)

根据(2)式，当ci(t)与yi(t)形成复共轭时，得到解析信号Ci(t)：

Ci(t)=ci(t)+iyi(t)=ai(t)eiθi(t)

(3)

其中ai(t)为瞬时振幅，θi(t)为相位，即：

(4)

(5)

相应的瞬时频率为：

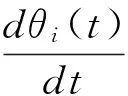
(6)

经EMD变换后所得的瞬时频率具有真正的物理意义。忽略残余分量r(t)，原序列可以重构为：

(7)

通过对本征模态函数做Hilbert变换，可得到各分量的瞬时振幅和瞬时频率，数据的瞬时性能通过它们很好地反映出来。如果把振幅显示在时间-频率上，就可以得到原序列的Hilbert谱。

Hilbert-Huang谱定义为：

(8)

Hilbert-Huang谱能反映幅值在整个频段上随频率和时间变化的规律，是一种完整的时-频分布。

3 渭河径流统计规律分析

渭河临潼水文站是黄河支流上的一个重要水文观测站，研究渭河的径流变化规律对于黄河抗洪防汛及治理有着重要的指导意义。径流变化规律分析的原始序列采用临潼站1961～2006年的年均流量序列。

采用经验模态分解方法对临潼水文站年平均径流序列进行分解，得到4个本征模态函数和一个残余趋势分量，如图1所示。

图1 年径流的经验模态分解

由图1可知，第一个本征模态函数IMF1的波长最短、振幅最大，与原序列保持较好的一致性，其包含的信息更能反映原序列的特征；从IMF1到IMF4呈现出振幅逐渐减小，频率逐渐降低，波长逐渐增大的趋势。则其对原序列的影响程度依次降低。

经验模态分解趋势项Residue表明临潼水文站年平均径流变化呈总体下降的趋势。将各本征模态函数和趋势项叠加，得到的序列与原序列状态保持一致，进一步说明该方法的精确度较高。

按照公式对临潼站年平均流量经EMD分解出的IMF进行Hilbert变换，得到中心频率(IMF序列变化后各点瞬时频率的平均值)、平均周期和平均振幅等统计结果，如表1所示。

表1 本征模态函数的统计特征值

从表1可以看出，临潼站年平均径流的本征模态函数IMF1～IMF4的中心频率逐渐降低，平均周期逐渐变长，平均振幅逐渐变小。表明渭河径流变化存在9.52年、13.70年、21.74年和41.67年的周期。这些周期的变化反映年径流在整个时域内变化的特性。

4 小结

HHT方法在处理非线性、非平稳数据时具有很强的自适应性，能够保留数据样本本身的特性，最后得到趋势分量和不同尺度的波动。它能够将叠加的复杂信号分解成有限个具有一定物理意义的内蕴模式分量函数，能够对瞬时频率特征进行定量的分析，从而得到瞬时频率和Hilbert时间频谱，与传统的时间序列分析方法相比更具有优越性。通过径流序列分析，得到水域径流变化规律，对防洪调度以及水利工程的修建具有重要指导意义。

[1]赵雪花．河川径流演变规律的挖掘与识别技术[D]．西安理工大学，2005．

[2]燕爱玲,黄强,刘招,等.R/S法的径流时序复杂特性研究[J].应用科学学报, 2007, 25(2): 214-217.

[3]Huang N E,Shen Z,Long S R,etal.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proc R Soc Lond A,1998,454(3):903～995.

[4]谭善文．多分辨希尔伯特-黄变换方法的研究[D]．重庆大学，2001．

[5]熊学军,郭炳火,胡筱敏，等．EMD方法和Hilbert谱分析法的应用与探讨[J]．海洋科学进展，2002，20(2)：12-21．

[6]Worrall F, Burt T P.Time series analysis of long-term river dissolved organic carbon records[J].Hydrological Processes, 2004, 18(5): 893-911.

RunoffLawAnalysisbyHilbert-HuangTransform

QIAN Hao1, ZHAO Yi2, XU Bo2, ZHENG Jun-yao2

(1.Zhang-fuhe Irrigation Water Supply Management Office, Handan Water Resources Bureau, Hebei Handan 056001, China;2.North China Institute of Water Resources and Electric Power, Zhengzhou 450011, China)

Compared with traditional analytical method of time series, Hilbert-Huang Transform has advantages to describe time-frequency characteristics for nonlinear, unsteady, weak-dependency and highly complex time series. Empirical Mode Decomposition (EMD) method is adopted to analyze time series, Intrinsic Mode Function (IMF) is reflected and the evolution of time series and sequence changes in the residual items (trend term) is obtained. Then, Hilbert - Huang transform is made for each IMF. The statistics reflected in runoff and sequence changes cycle are obtained. Taking hydrological stations of Lintong in the Wei River as examples, periods analysis of IMF shows that runoff change has period of 9.52,13.70,21.74 and 41.67 years, and gradually decreases.

Empirical Mode Decomposition; runoff law; hydrological stations of Lintong

TP18

A

1008-3715(2012)06-0113-03

(责任编辑赵冰)