一类非自治二阶系统的周期解

王少敏，熊 明，茶国智

（1.大理学院数学与计算机学院，云南大理 671003；2.大理学院工程学院，云南大理 671003）

一类非自治二阶系统的周期解

王少敏1，熊 明1，茶国智2

（1.大理学院数学与计算机学院，云南大理 671003；2.大理学院工程学院，云南大理 671003）

文章的主要目的是研究一类二阶哈密顿系统的周期解的存在性。通过使用最小作用原理获得了一个新的存在性定理。

周期解；最小作用原理；Sobolev's不等式

1 引言和主要结果

考虑二阶系统

其中T＞0，F：［0，T］×RN→R满足如下假设：

（A）：F（t，x）对于每个x∈RN关于t可测，对于a.e.t∈［0，T］关于x是连续可微的，存在a∈C（R+，R+），b∈L（10，T；R+）使得

H1T=｛u：［0，T］→RN｜u是绝对连续，u（0）=u（T），u∈L（20，T；RN）｝是一个Hilbert空间，具有范数

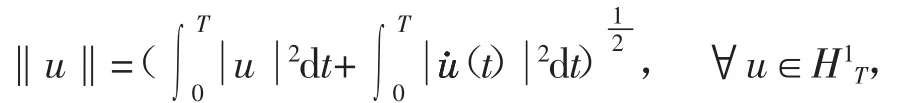
相应泛函为

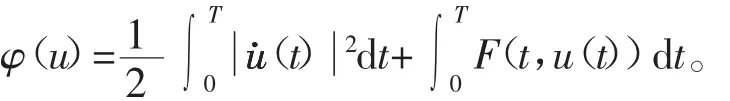
在H1T上连续可微且弱下半连续且

众所周知，u∈H1T是问题（1）的一个解的充要条件是u是φ的一个临界点〔3〕。

在假设（A）和一些适当的条件下，通过使用最小作用原理和临界点理论中的极大极小方法，人们已经获得了很多存在性结果〔1-10〕。特别地，文献〔2〕获得了如下定理。

则问题（1）至少存在一个周期解极小化φ。

由于受到定理A〔2〕的启发，我们获得了一个新的存在性定理，这个新结果推广了Ma〔2〕中的定理A，即α=2的情形。本文的主要结果如下。

则问题（1）至少存在一个周期解极小化φ。

2 定理的证明

由（3）式及Sobolev's不等式得

由（2）式及Wirtinger’s不等式得

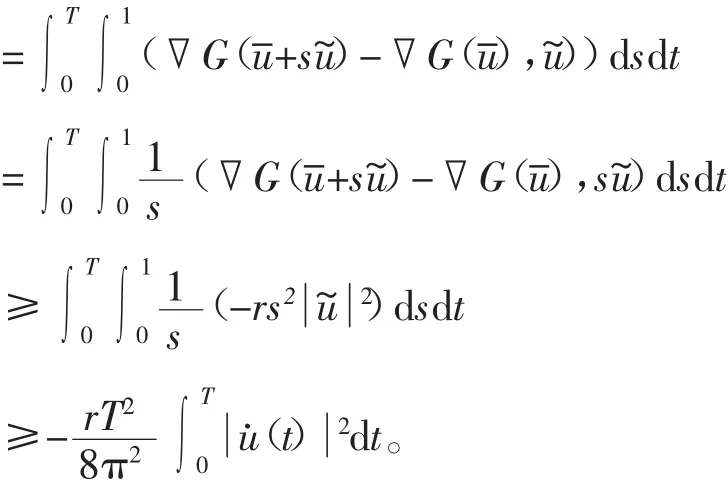
因此，有

所以φ（u）→+∞（‖u‖→∞）。因此，φ在H1T上达到极小。由文献〔3〕中的定理1.1和推论1.1，完成了证明。

〔1〕Tang C L.Periodic solutions for non-autonomous second order systems with sublinear nonlinearity〔J〕.Proc.Amer.Math.Soc.，1998（126）：3263-3270.

〔2〕Ma J，Tang C L.Periodic solutions for some nonautonomous second-order systems〔J〕.J.Math.Anal.Appl.，2002（275）：482-494.

〔3〕Mawhin J and Willem M.Critical Point Theory and Hamiltonian Systems〔M〕.Berlin:Springer-Verlag，1989.

〔4〕Tang C L.Periodic solutions for non-autonomous second order systems with sublinear nonlinearity〔J〕.Proc.Amer.Math.Soc.，1998（126）：3263-3270.

〔5〕Tang C L.Periodic solutions of non-autonomous second order systems with quasisub-additive potential〔J〕.J.Math.Anal. Appl.，1995（189）：671-675.

〔6〕Tao Z L，Tang C L.periodic and subharmonic solutions of second order Hamiltonian systems〔J〕.J.Math.Anal.Appl.，2004（293）：435-445.

〔7〕Tang C L.Periodic solutions of non-autonomous second order systems〔J〕.J.Math.Anal.Appl.,1996（202）：465-469.

〔8〕Wu X P，Tang C L.Periodic solutions of a class of non-autonomous second order systems〔J〕.J.Math.Anal.Appl.，1999（236）：227-235.

〔9〕Rabinowitz P H.On subharmonic solutions of Hamiltonian systems〔J〕.Comm.Pure Appl.Math.，1980（33）：609-633.

〔10〕Tang C L，Wu X P.Periodic solutions for second order systems with not uniformly coercive potentia〔lJ〕.J.Math.Anal. Appl.，2001（259）：386-397.

Periodic Solutions for Some Non-autonomous Second Order Systems

WANG Shaomin1,XIONG Ming1,CHA Guozhi2
（1.College of Mathematics and Computer,Dali University,Dali,Yunnan 671003,China; 2.College of Engineering,Dali University,Dali,Yunnan 671003,China）

The purpose of this paper is to study the existence of periodic solutions of a class of second order Hamiltonian systems. One new existence theorem is obtained by using the least action principle.

periodic solutions;the least action principle；Sobolev's inequality

O177［文献标志码］A［文章编号］1672-2345（2012）04-0011-03

云南省教育厅科学研究基金项目（09Y0367）

2011-06-17

王少敏，副教授，主要从事非线性分析研究.

（责任编辑 袁 霞）