基于格的公钥加密体制的研究
2012-11-01王励成何万生
潘 平,王励成,何万生
(北京邮电大学 计算机学院,北京 100876)
引 言
公钥密码的思想由Diffie和Hellman提出以来,许多实用的公钥密码体制被建立并得以广泛的研究.这些体制的安全性大都依赖于数学中的某些难解问题.目前广泛使用的两类公钥密码体制:RSA体制及其变种和ElGamal体制及其变种,其安全性分别基于大整数分解问题和离散对数问题.然而,人们已经找到了这些问题的多项式时间的量子算法攻击方法,这意味着在量子计算机时代,这些密码体制的安全性面临威胁.于是,人们开始积极寻求新的公钥密码体制的实现平台,并设计新的能够抵抗量子算法攻击的密码方案(即后量子密码,Post-quantum Cryptography)已经成为密码学研究的前沿课题.
目前,后量子密码的研究方向主要包括:基于哈希的密码体制、基于编码的密码体制、基于格的密码体制、基于多变量的密码体制等等.其中,基于格的公钥密码体制的研究和应用取得了喜人的成果和发展.比如著名的 AD 体制[1](1997)、GGH 体制[2](1997)、NTRU体制[3](1998)、Regev体制[4](2005)、GPV体制[5](2008)、Peikert体制[6](2009)等等.这些体制的安全性分别基于格的最近向量问题(CVP)、最短向量问题(SVP)、uSVP问题、错误学习问题(LWE)、最小整数解问题(SIS)等等.
格是一种典型的线性代数结构.由于格丰富的组合结构,使得格成为近年来计算科学领域中活跃的研究课题.1996年,Ajtai[7]发现了某些格问题的最坏情形复杂性与平均情形复杂性之间的联系,从而引发了对格问题复杂性的一系列研究,使得格在密码学中得以广泛的应用,出现了许多基于格难题的密码体制(以下简称格基密码体制).
利用格构建公钥密码体制之所以吸引人,其主要原因有两方面:(1)格基密码体制的安全性可规约于最坏情形下特定格问题的难解性.也就是说,攻破了这些格基密码体制意味着能求解其相应格难题的所有实例;(2)格基密码体制的加解密速度非常快.
1 格上的密码学难题
1.1 格的相关概念
格是m维空间中具有周期性结构离散点的集合.具体定义如下:
定义1(格)设Rm是m维欧式空间,设向量b1,…,bn是n个线性独立的m维向量(m ≥ n),格定义为:

向量b1,…,bn称为格的一组基.几组不同的线性无关向量可表示同一个格,此时这几组向量都称为格基.可用矩阵表示格,设B=(b1,…,bn)ÎRm×n,则格L(B)={Bx—xÎZn}.
当n=m时,称格L(B)是满秩或满维的.以下如无特别说明,均为满维格.
定义2(对偶格)任意格基BÎRn×n,定义对偶格为:
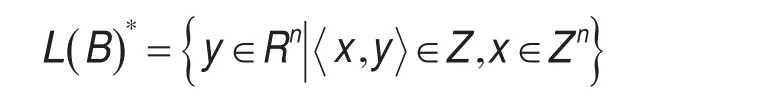
则 L(B)*=L((B-1)T).
定义3(q元格)设AÎZqn×m是n×m矩阵,q,m,n是整数,两个m维q元格定义为:

定义4(理想格)设n是2的幂次方,f是有理数域Q上的不可约多项式,如f=xn+1.设R=Z[x]/f,I是R的非零理想,则满足的整数格L(B)称为理想格.
m维空间中的格点也可看作是m维向量,称为格向量.对于格向量,可定义不同的范数,如2-范数(也称欧氏范数),p-范数,无穷范数等.以下如无特别说明,均视为2-范数,即格向量a=(a1,…,an)ÎRn,其范数定义为

1.2 格上难题
下面介绍几种典型的计算型格问题:
最短向量问题(SVP):给定格基BÎZm×n,找格中的非零向量 Bx(xÎZn),使得对任意的非零向量满足
最近向量问题(CVP):给定格基BÎZm×n和目标向量tÎZm,找格中的非零向量Bx(xÎZn),使得对任意的 yÎZn,满足‖Bx-t‖≤‖By-t‖.
uSVP问题:给定格基BÎZn×n,找格中的非零向量v,使得v是唯一最短向量,且长度至多是v的nc倍的其他向量都平行于v.
最短独立向量问题(SIVP):给定格基BÎZn×n,找n个线性独立的格向量S=(s1,…,sn)(1≤i≤n),使得最小.
R-LWE问题:设n是2的幂次方,f(x)=xn+1Î Z[x],q=1mod 2n是大素数模.设Rq=Zq[x]/<f(x)>为模f(x)和模q的所有整系数多项式环,s=s(x)ÎRq,随机选择aÎRq,e取自Rq上的某个高斯分布,输入一对(a,as+e),计算s.
2 基于格的公钥加密体制
目前为止,基于格的公钥加密体制研究取得了显著的成就.如公钥密码体制[1]和有可证明安全的加密体制,[8]基于身份的加密体制[5-6],[10-11],全同态密码体制[12]等.这些密码体制的构造分为两类:一类体制效率高、实用性强,但没有可证明安全性;另一类体制虽然其安全性证明是基于最坏情形下的格问题的困难性,理论上也有效,但不实用.
下面介绍几种著名的基于格的公钥加密体制.
2.1 基于uSVP的公钥加密体制
Ajtai和Dwork[1]在1997年首次提出了最坏情形下基于O(n8)-uSVP难题的公钥密码体制.随后Goldreich等人[2]提议如何消除AD方案中存在的解密错误,并将该方案改进到O(n7)-uSVP.在2004年Regev[4]提出的基于O(n1.5)-uSVP加密方案相当简单,仅有整数模运算,有很强的安全性.但是以上几个公钥密码体制的效率很低,公钥长度太长,密文扩展也太大.
Ajtai和Dwork设计了三种版本的新型公钥密码算法AD1、AD2和AD3,统称为AD密码算法[1].其描述如下:
密钥生成:如果u是uSVP格的最短向量,那么可由u确定一组超平面,这组超平面作为私钥.然后通过一些特殊的方法,生成与这组超平面很接近的一个空间点,这个点就是公钥.根据这个点找出其超平面的难度等价于求解最坏情形下的uSVP问题.
加密:按逐比特进行加密.加密0时,通过公钥找到某个超平面附近的一个随机向量,然后对这个向量在一个很小的领域内进行扰动,扰动后的向量就是0的密文.加密1时,随机地从空间中选择一个向量,这个向量就是1的密文.
解密:用私钥(超平面)检查密文对应的点是否足够靠近某个超平面.如果是,则解密为0,否则为1.
显然,AD存在解密错误的可能.对0加密后总能解密成0,但对1的加密有可能被解密成0,发生解密错误.但可以选取适当的参数,降低AD体制解密失败的概率.
Regev[4]公钥加密体制如下所示:
解密:如果密文除以N/h的余数很小时,解密为0,否则为1.因为a1,…,am均离N/h的整数倍数很近,则0的密文∑iÎSai也离N/h的整数倍数很近.因此0的密文能被正确地解密;同样,远离N/h的倍数,那么1的密文也远离N/h的倍数.从而可以正确解密为1.当然,这个方案也存在解密错误.
2.2 基于CVP的公钥加密体制
1997年Goldreich等人[2]提出基于CVP难题的GGH密码体制,GGH是最直观的基于格的公钥密码体制.该体制的密文是将对应于明文的格向量加上一个随机噪声向量而得;公钥和私钥是同一个格中的两种不同表示.私钥具有特殊的结构,它允许在一定界限下消去噪声向量.
GGH公钥加密体制描述如下:
密钥生成:私钥为一个“好”的格基B,即由短且几乎正交的向量组成.从数学意义上讲,如果输入是一个良好的规约基,则可在较短时间内准确地找到靠近目标向量的格点.即有效求解近似CVP问题的某个实例.公钥是一个“坏”基H,使得L(H)=L(B),即公私钥是同一个格的两个不同基.
加密:消息为格点v,加上随机产生的扰动向量r,形成的密文为c=v+r.

GGH密码体制没有达到语义安全,因为其加密过程是确定型的(即很容易区分出密文所对应的明文).即使取适当大的安全参数,GGH密码体制也容易被攻破,因而实际上GGH是不安全的.另外,GGH也存在解密错误现象.GGH选择体制参数可使出现解密错误的概率控制在10-5以下.
2.3 基于LWE及R-LWE的公钥加密体制
在2005年,Regev[4]提出LWE问题并证明在适当假设下LWE问题是难解的.第一,LWE在目前最好的算法下是指数级的运行时间;第二,LWE是LPN(错误奇偶校验学习)问题的扩展,而LPN在机器学习领域中认为是难的;第三,LWE与最坏情形下的某些格问题一样难,如,近似SVP和近似SIVP.
近年来,LWE在密码构造中有着非常广泛的应用.如选择明文安全(CPA)的加密方案:Regev05[4],PVW08[13]等;选择密文安全(CCA)的加密方案:PW08[9],Pei09[6]等;不经意传输协议 PVW08[13];基于身份的加密方案:BCHK06[14],GPV08[5],ABB09[10]等;密钥泄露容忍的加密方案:GPV08[5],AGV09[15],GKPV10[16]等.LWE问题之所以有很强的吸引力,除其能够抵抗量子算法攻击外,还具有高效性和低复杂性的运算(主要是加法).
2.3.1 基于LWE的公钥加密体制
Regev[4]构造了第一个基于LWE的可证明安全的密码体制.后来,Peikert等人[13]给出基于LWE的多比特的PVW公钥密码体制,其在时间和空间效率上都有很大的改进.
Regev公钥加密体制如下所示:
体制参数:设m,n,p均是整数,χ是Zp上的概率分布.
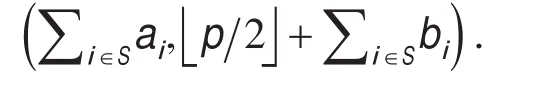
Regev公钥加密体制的公钥长度为O(n2),在加解密中每加密一比特需要Õ(n2)比特的运算,每加密一比特扩展了Õ(n).
PVW公钥加密体制描述如下:
体制参数:设m,n,p,l是整数,q> p是素数.对每一个vÎZp(即一个消息的一个坐标),定义v的“补偿”为ω(v)=「v·q/p」ÎZq.χ是Zp上的概率分布.设R≤q是整数,定义行向量的集合 ℜ =[0,R-1]1×m⊆ Zq1×m.
密钥生成:随机选择矩阵SÎZqn×l,S为私钥.随机选取矩阵AÎZqm×n和EÎZqm×l,其中E中的每一个元素ei,j服从分布χ.公钥为一对(A,B=AS+E)ÎZqm×n×Zqm×l.
加密:对于表示成行向量的待加密消息 vÎZq1×l,ω=ω(v)ÎZq1×l.选择一个行向量rÎℜ ÌZq1×m,密文为(u,c),这里 u=rAÎZq1×n,c=rB+ωÎZq1×l.
解密:对于私钥S和密文(u,c),计算d=c-uSÎZq1×l,然后输出明文 vÎZq1×l,使得v中的每一个元素 vi满足di-ω(vi)ÎZq离0 mod q最近.
PVW公钥加密体制在时间和空间效率均改进到线性因子.特别是,在加解密中每加密一比特只需Õ(n)比特的运算,每加密一比特扩展到O(1).以上两个方案比AD公钥密码体制好,但在公钥长度上仍不理想.
2.3.2 基于R-LWE公钥加密体制
LWE已经成为密码构造的主要部分.基于LWE的密码方案常常需要相当大的密钥长度,通常是n2阶.2010年,Lyubashevsky等人[17]提出LWE的代数变种,R-LWE,并证明:假定不存在多项式时间的量子算法能够求解理想格上的最坏情形问题,则R-LWE的分布是伪随机的;同时给出第一个真正实用且有效的有可证明安全的公钥密码体制.他们预言R-LWE问题的代数结构可能会引起新的密码应用.
下面介绍基于R-LWE的公钥加密体制:
体制参数:设f(x)=xn+1ÎZ[x],其中n是2的幂次方,q=1mod 2n是大素数模.R=Z[x]/<f(x)>为模f(x)的所有整系数多项式环,设Rq=Zq[x]/<f(x)>为模f(x)和模q的所有整系数多项式环.
密钥生成:设m是安全参数,元素aiÎRq.选择m个“小”riÎR.计算am+1=∑iÎ[m]ri·aiÎRq.公钥为a1,…,amÎRqm+1,私钥为r1,…,rm,rm+1=-1 ÎRm+1.
加密:加密n比特消息zÎ{0,1}n,随机选择sÎRq,ei服从Rq的某个分布.对于每一个iÎ[m],计算

则密文为b1,…,bm+1ÎRqm+1.
解密:待解密密文b1,…,bm+1ÎRqm+1和私钥 r1,…,
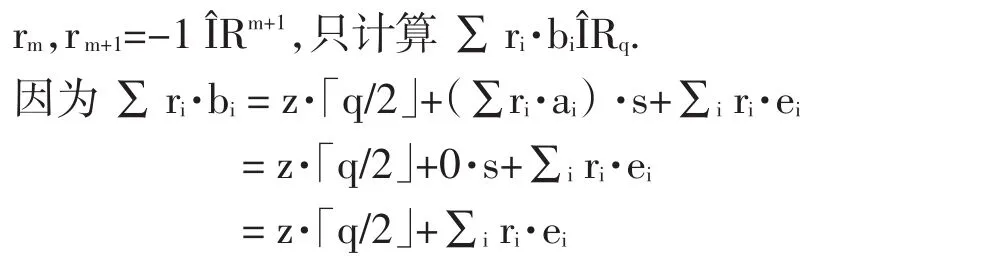
以上方案只需Zq上的O(n)个元素,利用快速傅里叶变换,可以使得向量上的运算速度更快,从而其密码构造有小的密钥且运算速度也相当快.
NTRU方案是Hoffstein,Pipher和Silverman提出的目前很实用的加密方案.但是,NTRU没有可证明安全,也遭到各种攻击.最近,Stehlé和Steinfeld[18]结合NTRU公钥密码体制和R-LWE思想,通过以下几点改进,使得改进后的NTRU在理想格上最坏情形格难题下达到CPA安全,并给出可证明安全.
第一,改进的NTRU是基于环R=Z[x]/<xn+1>而不是RNTRU=Z[x]/<xn-1>的加密体制.
第二,选择素数q使得f=xn+1mod q有n个不同的线性因子,即q=1mod 2n.这样使得在Rq=R/q上搜索型R-LWE可以规约到判定型R-LWE,p仍取2.
第三,f,g取样于R的离散高斯分布,其中f满足f=1mod p,设f在模q下的逆元为fq-1,私钥为fÎRq,h=pg fq-1mod q,公钥为hÎRq.
第四,在原加密算法中加上一个小扰动e,密文为c=m+rh+pe mod q,这里r,e是取样于R-LWE的错误分布.
第五,解密简化为m=(fc mod q)mod p.
改进后的NTRU加、解密Ω(n)比特明文时只需Õ(n)比特运算,就能获得抗 2g(n)-time攻击的安全,这里g(n)介于Ω(log n)和о(n)之间.
R-LWE的代数结构给基于格的密码设计的真正实用性带来了很大的希望,同时也在密码领域中引起了格理论的进一步发展.
3 基于身份的加密体制
最早提出基于格的身份加密(IBE)方案是Gentry等人.[5]随后 Peikert,[19]Agrawal等人,[10]和 Cash等人[20]先后提出了安全、有效的基于格的IBE/HIBE方案.
Gentry等人[5]表明:在Regev公钥加密体制中,公钥是靠近格点的某些点,这些点在格空间是指数级稀疏的.相比之下,密文在空间上是均匀分布的.但是如果要构造IBE体制时,那么在Regev公钥体制中如何把身份映射为有效的公钥呢?为此Gentry等人提出简单解决此问题的办法,即Regev公钥加密体制的“对偶”体制,称为DualRegev公钥加密体制,其本质是对公钥和密文进行交换.以DualRegev公钥加密体制为主要部分,构造了随机预言模型下基于LWE的匿名安全的IBE体制.另外,他们又提出新的陷门原语概念,称为原像可取样陷门函数.这个陷门函数与随机预言模型下几个著名签名方案中的陷门置换相比,其功能更强.
Peikert[19]在2009年提出新的基于格的密码原语,称为盆景树(bonsai tree)技术,并利用这个技术构造了不依赖于双线性配对的HIBE方案(标准模型下).Peikert表明该方案的安全性是基于标准的LWE且是等级匿名的.就是说,从计算上看,密文隐藏了被加密的身份.
随后,Agrawal和Boyen[10]构造了标准模型下基于随机整数格上LWE问题的IBE体制.该体制具有伪随机密文的匿名性.文献[10]给出IND-sID-CPA安全(即选择性ID、选择明文攻击下达到不可区分)的IBE,利用身份的比特分解可以得到完全自适应性ID安全的IBE.也表明利用指数规约或组合变换,可以得到更有效的IND-ID-CPA安全的IBE方案.
接着,Cash,Hofheinz和Kiltz[20]提出一个新的密码原语,称为基授权,即允许一个人通过安全方式用给定格的一个短基来导出相关格的新的短基.本质上来说这些短基的作用类似于密码中的陷门.基授权技术的主体思想被认为是GPV的原像可取样思想的一般化,有着更灵活、更广泛的应用.从技术层次上看,基授权技术等价于Peikert的盆景树技术.利用基授权技术,他们得到了如下几个新的构造:第一,构造了第一个标准模型下有可证明安全的无状态数字签名方案和IBE方案,其安全性是基于最坏情形下的LWE.第二,构造了随机预言模型下有可证明安全的相当高效的HIBE,其安全性是基于最坏情形下的LWE.这个构造利用基授权实现了密钥的阶层.第三,构造了同样难题假设下无随机预言模型的可证明安全的HIBE方案.他们认为可以利用BCHK[14]的变换将CPA安全的d-HIBE转换成CCA安全的(d-1)-HIBE.
文献[5]中的IBE/HIBE方案都是把身份看成是一系列比特数,对每一比特分配一个矩阵.这样的加密体制是相当完美的,但是与随机预言模型下的GPV加密方案相比,还是很低效的.2010年,Agrawal等人[10]构造IBE体制时,把身份看成块,产生与GPV体制中随机预言模型下相同维数的格,将格分为“左”格和“右”格.“左”格的陷门只作为体制的主密钥,可以为所有的身份生成私钥.“右”格的陷门只用在安全性证明中,使得模拟器为所有身份生成私钥,当然除挑战的身份外.另外,一般的基于格的密码体制是定义在相对小的域Zq,这样使得编码后的身份取自于1,…,q,导致体制的身份太少.在方案中把身份看成Zqn上的向量(共有qn个身份),然后利用编码函数H映射成Zqn×n上的矩阵,这里H是单射以便在安全性证明中,对于不同的身份,其哈希值的差值绝不能是单数.该方案与Cash等人的IBE方案[20]相比,其密文更短、更简洁.另外也可利用基本的格基委托技术,将基本的IBE转化成HIBE.
4 总结
最初以LLL算法[21]为标志的格基技术是作为一种密码分析工具展示了其威力,但10年后,格基技术作为一种崭新的密码设计平台而备受关注.如今,格成为最看好的后量子密码体制之一.这种繁荣正如双线性配对技术[22]最初也是作为一种密码分析工具而出现,随后在密码设计上大放异彩.因此,格基技术在密码设计上的应用将会更加丰富多彩.当然,为了使格基密码体制最终走向实用,还有许多工作要做.一方面,许多格问题的困难性需要进一步的研究;同时,减少格基密码的密钥长度、追求更加高效的设计,永远是值得大力研究的课题;最后,尝试设计人们期待已久的基于其它数学平台而未能获得的密码方案,也许最能显示格基密码的独特魅力.比如基于格的全同态加密方案的成功设计.[12]
[1]AJTAI M,DWORK C.A public-key cryptosystem with worstcase/average-caseequivalence[C].STOC,1997:284-293.
[2]GOLDREICH O,GOLDWASSER S,HALEVI S.Public-key cryptosystems from lattice reduction problems[J].Advances in cryptology,LNCS1294.Sci.,1997:112-131.
[3]HOFFSTEIN J,PIPHER J,SILVERMAN J H.NTRU:a ring based public key cryptosystem[C].ANTS-III,LNCS 1423,1998:267-288.
[4]REGEV O.On lattices,learning with errors,random linear codes,and cryptography[C].STOC,ACM,2005:84-93.
[5]GENTRY C,PEIKERT C,VAIKUNTANATHAN V.Trapdoors for hard lattices and new cryptographic constructions[C].STOC,ACM,2008:197-206.
[6]PEIKERT C.Public-key cryptosystems from the worst-case shortest vector problem[C].STOC,2009:333-342.
[7]AJTAI M.Generating hard instances of lattice problems[C].STOC,1996,(13):1-32.
[8]REGEV O.New lattice-based cryptographic construction[J].ACM,2004,51(6):899-942.
[9]PEIKERT C,WATERS B.Lossy trapdoor functions and their applications[C].STOC,ACM,2008:187-196.
[10]AGRAWAL S,BONEH D,BOYEN X.Efficient lattice(H)IBE in the standard model[C].EUROCRYPT,2010:553-572.
[11]PEIKERT C.Bonsai trees(or,arboriculture in lattice-based cryptography)[J].Cryptology ePrint Archive,Report 2009:359,http://eprint.iacr.org/.
[12]GENTRY C.Fully homomorphic encryption using ideal lattices[C].STOC,2009:169-178.
[13]PEIKERTC,VAIKUNTANATHANV,WATERSB.Aframework for efficient and composable oblivious transfer[C].CRYPTO,2008:554-571.
[14]BONEHD,CANETTIR,HALEVIS,KATZJ.Chosen-Ciphertext Security from Identity-Based Encryption[J].SIAM Journal on Computing,2006,36(5):915-942.
[15]AKAVIA A,GOLDWASSER S,VAIKUNTANATHAN V.Simul-taneous hardcore bits and cryptography against memory attacks[C].TCC,2009:474-495.
[16]GOLDWASSER S,KALAI Y,PEIKERT C,VAIKUNTANATHAN V.Robustness of the learning with errors assumption[C].ICS,2010.
[17]LYUBASHEVSKY V,PEIKERT C,REGEV O.On Ideal Lattices and Learning with Errors over Rings[C].EUROCRYPT 2010,LNCS 6110,2010:1-23.
[18]STHLEAND D,SREINFELD R.Making NTRU as secure as worst-case problem over ideal lattices[C].EUROCRYPT 2011,Publisher:Springer Berlin Heidelberg,6632:2011:27-47.
[19]PEIKERT C.Bonsai trees(or,arboriculture in lattice-based cryptography)[J].Cryptology ePrint Archive,Report 2009:359,http://eprint.iacr.org.
[20]CASH D,HOFHEINZ D,KILTZ E.How to delegate a lattice basis[J].Cryptology ePrint Archive,Report 2009/351,2009.http://eprint.iacr.org/.
[21]LENSTRA A K,LENSTRA H W,Jr.,LOVSZ L.Factoring polynomials with rational coefficients[J].Math.Ann.,1982,261(4):515-534.
[22]SAKAI R,OHGISHI K,KASAHARA M.Cryptosystem based on pairings[J].SCIS 2001,Oiso,Japan.
