不规则采样数据广义线性反演算法的改进

刘保童，李桂花

（1.天水师范学院 物理与信息科学学院，甘肃 天水 741001；2.山东科技大学 地质科学与工程学院，山东 青岛 266590）

引言

谱分析是一个非常活跃的研究领域，可能的应用相当广泛，详细的介绍可从参考文献[1]中看到.从本质上讲，谱分析是一个欠定的线性反问题，它可用于从非均匀采样点重建信号，这时，算法从非均匀采样信号估计离散傅里叶变换（DFT），最后用反DFT得 到 均 匀 采 样 的 信 号.Oldenburg（1976）把Backus-Gilbert线性反演理论应用于具有噪声和空缺数据的傅里叶变换，Sacchi et al.（1998）提出了一种利用贝叶斯（Bayesian）方法的傅里叶变换反演方法，针对稀疏分布傅里叶系数的估计，他们在迭代反演中使用了先验柯西（Cauchy）概率密度函数.在DFT反演地震道重建方面，Duijndam et al.（1999）利用了一个与空间采样间隔相对应的对角规则化矩阵使不规则采样数据的DFT反演稳定化，这是在数据空间中使用约束.[2]Wang（2003）利用由初始的DFT估计所计算的模型的协方差矩阵作为对角加权矩阵，给出了一种稀疏约束最小平方反演方法，所不同的是在模型空间中使用约束.[3]本文从Moore-Penrose广义逆的角度讨论DFT谱估计这一线性反演问题，在算法中引入了一个实对角正定约束矩阵，用低频分量的傅里叶图像对高频傅里叶图像的估计进行约束，提高了模型空间的分辨率.作者在微型计算机上编写程序实现了这一算法，用有空缺道的不规则采样多道记录模型进行数值计算试验，证明该方法是有效的.

1 DFT线性反演理论

定义连续正向空间傅里叶变换为

式中x是空间变量，kx是波数，而ω=2πf，f是时间频率.反变换由下式给出

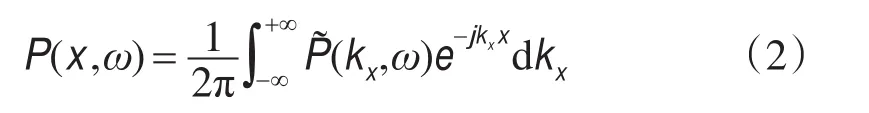
时间傅里叶变换对用类似的方式定义，只不过指数所用符号的约定不同.对于沿x规则采样的带限数据，众所周知，与（1）式有关的离散傅里叶变换（DFT）为

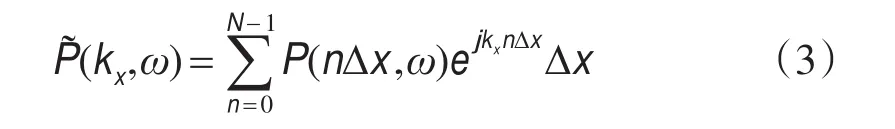
其中Δx的选择应足够小以避免空间傅里叶域假频.在不规则采样的情况下，一种获得傅里叶域数据的直接方法是使用黎曼和（the Riemann sum），（1）式中的积分用一个与实际采样位置（x0，x1，…，xN-1）对应的和来代替：

式中Δxn定义为

ln=(xn+xn-1)2是两个样点之间的中心点.我们称变换（4）为非均匀离散傅里叶变换（NDFT），NDFT不能精确地还原重现傅里叶谱.

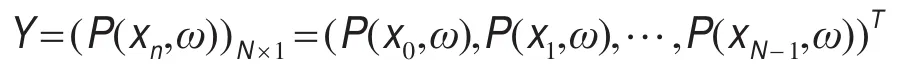
为已知的非均匀数据

现在考虑采样间隔为Δkx，数据带限区间在[-MΔkx，MΔkx]总共有Mp=2M+1个样点的一个规则采样傅里叶域，对任一空间位置xn，与NDFT对应的离散反傅里叶变换由下式给出

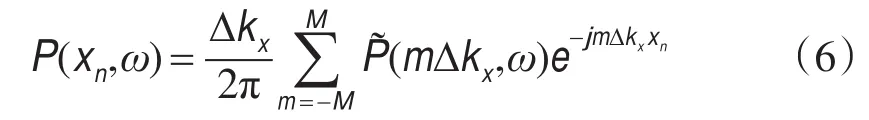
且是精确的，Δkx的选择应足够小以避免空间x上的假频.将不规则空间采样位置 (x0，x1，…，xN-1)所对应的方程（6）的N个式子结合起来可写成矩阵形式

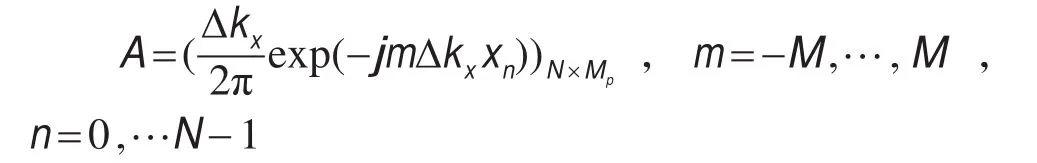
利用（7）式求P～是一个线性反演问题，存在解的非唯一性.

由于A是一个N×Mp的矩阵，A的逆应该用Moore-Penrose广义逆来求解.[4]当N＞Mp，即方程（7）为超定方程时，（7）式的最小方差解

当N＜Mp，即方程(7)为欠定方程时，(7)式的最小范数解

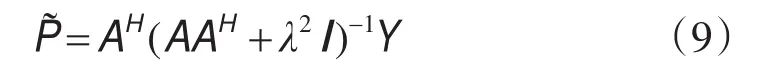
式中λ为阻尼因子，一般取0.1～1即可.(AAH+λ2I)-1等价于一个反褶积算子，它提高了变换域的分辨率.但（8）、（9）式给出的这个反演解还不够理想，分辨率仍不能满足信噪分离和数据重建的要求，因此，寻求反问题（7)式的具有更高分辨率的解显得非常重要.

事实上，方程（7）的求解是一个不适定的反问题，因而只能通过加先验约束来实现，且一般都要迭代.[1]本文下面给出一种非迭代的反演解，可有效地提高变换分辨率，是对（8）、（9）的改进.

2 反演解的改进

由前面的分析可知，反问题（7）是一个约束的欠定最小平方问题，因此，按照广义最小平方理论[5]，本文给出（7）的一个解

式中，G=(gil)Mp×Mp是一个实对角正定约束矩阵，其对角元素为

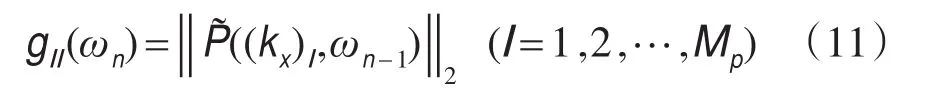
这种非迭代的直接处理方法能够将输入数据的单色波分解聚焦到其最大的谱成分上.类似的思想也可用于改进Radon变换的分辨率.[6]

一旦使用改进的反演方法获得了尖锐的DFT谱，我们就可以对它实现反傅里叶变换产生数据空间中期望的规则采样输出.

3 数值计算试验

图1是一个理论合成二维数据体，共60道，道间距20米，时间采样率2毫秒，有三个同相轴.为了检验本文提出的方法的有效性，将图1中的13道记录数据去除，即假设已知图2所示的缺失不规则采样数据，我们要由它来重建恢复规则采样的完全数据.为看清楚缺失道所在的位置，在缺失数据的位置处填充零道，见图3.如用普通的最小平方反演解（9）式来重建，所得到的结果显示在图4中，与图3中的记录比较很容易看出，这一结果实际上等价于在缺失样点位置处插入了零道.这和理想结果（图1中的记录）相差甚远.现在用本文提出的算法，由图2中的记录来重建非均匀数据，利用（10）式估计的F-K谱显示在图6中，而利用非均匀离散傅里叶变换（NDFT）所得到的图2中记录的F-K谱如图5所示，显然，改进后的算法使估计出的DFT谱具有很高的分辨率.利用图6中尖锐的F-K谱，通过反傅里叶变换就可以产生数据空间中期望的规则采样输出，重建结果显示在图7中，它与图1中显示的期望输出符合的很好.

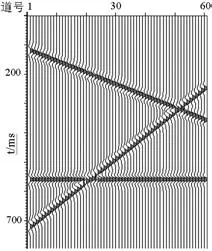
图1 理论合成记录

4 结论

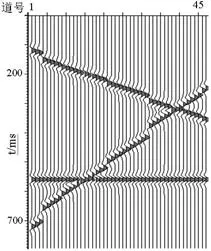
图2 已知的不规则采样数据

图3 在缺失数据的位置处填充零道

图4 普通的最小平方反演解重建结果

图5 用NDFT所得到的图2中记录的F-K谱

不规则采样或缺失数据的傅里叶重建是数据正则化处理的主要方法之一，本文从Moore-Penrose广义逆出发，采用最小平方线性反演方法估计DFT谱，在解中引入了一个实对角正定约束矩阵对普通的最小平方算法做了改进，提高了模型空间的分辨率.

图6 由改进的线性反演解所得到的图2中记录的F-K谱

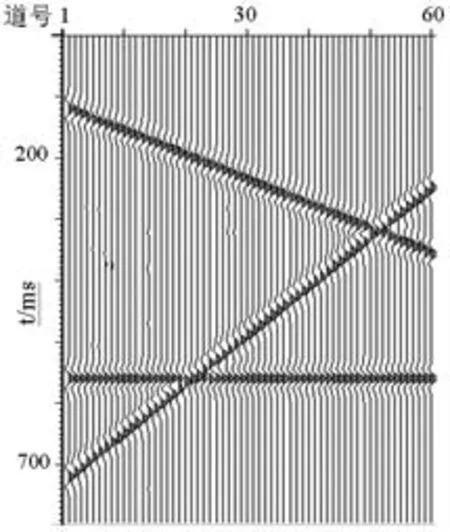
图7 用本文提出的改进反演解重建所得结果

[1]SACCHI M D,ULRYCH T J,and WALKER C J.Interpolation and extrapolation using a high-resolution discrete Fourier transform[J].IEEE Transactions on Signal Processing,1998,46(1):31-38.

[2]DUIJNDAM A J W,SCHONEWILLE M A,and HINDRIKS C O H.Reconstruction of band-limited signals,irregularly sampled along one spatial direction[J].Geophysics,1999,64(2):524-538.

[3]YANGHUA Wang.Sparseness-constrained least-squares inversion:Application to seismic wave reconstruction[J].Geophysics,2003,68(5):1633-1638.

[4]张贤达.矩阵分析与应用[M].北京:清华大学出版社,2004.

[5]TARANTOLA A.Inverse problem theory:Methods for data fitting and model parameter estimation[M].Elsevier Science Publ.,1987.

[6]刘保童,朱光明.一种频率域提高Radon变换分辨率的方法[J].西安科技大学学报,2006,26(1):112-116.