斜轴墨卡托投影的长度变形分析

2012-10-27中铁大桥局集团第一工程有限公司李付伟

河南科技 2012年4期

关键词：椭球面椭球纬度

中铁大桥局集团第一工程有限公司李付伟

96251部队刘灵杰

中铁大桥局集团第一工程有限公司王晓智

斜轴墨卡托投影的长度变形分析

中铁大桥局集团第一工程有限公司李付伟

96251部队刘灵杰

中铁大桥局集团第一工程有限公司王晓智

一、斜轴墨卡托投影

在工程测量中，经常需要对地面点的投影进行计算，以获得工程测量必需的数据。地面点投影的实质是双重投影，即先进行球面投影，再沿路线方向进行斜轴墨卡托投影。具体投影主要有两种方法：一是先将地面点归算至相应的参考椭球面，再将参考椭球面点投影到球面；二是直接将地面点投影至球面，之后进行斜轴墨卡托投影。

斜轴墨卡托投影作为地面点投影计算的重要步骤，其计算的精度将直接影响最终的结果。无论是将地面点投影至参考椭球面，再将参考椭球面点投影至球面；还是直接将地面点投影至球面，再进行斜轴墨卡托投影，每一步都将产生长度变形。本文，笔者分析了球面投影的长度变形，并比较了斜轴墨卡托投影和高斯投影的变形情况，总结了斜轴墨卡托投影长度变形的大小和规律，对工程测量具有指导作用。

一、球面投影的长度变形

1.投影点在参考椭球面上投影时的长度变形分析。球面投影公式如下：

式（1）中，λ为球面经度，L为参考椭球面经度，φ为球面纬度，μ为参考椭球面投影至球面的长度变形，R为测区平均曲率半径，B为参考椭球面纬度，N为卯酉圈曲率半径，ω为角度变形。α，U和K分别按下式计算。

式（2）、（3）和（4）中，B0为参考椭球面平均纬度，e为第一偏心率，φ0为测区平均纬度经球面投影后的纬度（φ0＝arcsin（sinB0）/α），U0按下式计算。

在同一参考椭球面上，球面投影长度变形与测区平均纬度B0和投影点纬度B有一定的关系，而与经度无关。取测区平均纬度B0的平均曲率半径作为投影球面半径，若球面投影在平均纬度为B0的纬线圈上没有变形（长度比μ＝m＝n＝1，面积比p＝1，ω＝0），则称B0为该纬线的标准纬线。

取WGS–84为参考椭球参数，测区平均椭球面纬度取B＝33°00′00″，假设地面点在参考椭球面上。随着纬度变化，球面投影长度也不断变化。两者变形情况见表1。

表1 点位于参考椭球面上、纬度变化时球面投影长度变形统计

由表1可知，取标准纬度线B0＝33°，在纬度相差4°、南北距离达440 km的情况下，当投影点投影到参考椭球面上时，球面投影长度变形最大只有0.009/100 000。对于一些普通工程测量来说，要求投影长度的标准变形不大于1/40 000；因此在有些工程测量中，该长度变形可以忽略不计。

2.当投影点不在参考椭球面上，而在不同高程面上时对投影长度变形的影响。

（1）当地面点平均大地高不大时，直接将地面点地理坐标投影至由相应参考椭球参数和测区中心纬度计算出的球面上。由式（1）可知：

式（6）中，R＝c0/（1＋e′2cos2B0），为测区中心点（B0，L0）处的平均曲率半径，式中c0为（B0，L0）处椭球极曲率半径；N＝c/（1＋e′2cos2B）1/2，为投影点位置处卯酉圈的曲率半径，式中c为投影点处的极曲率半径。

对于某一测区来讲，α为常数，令ν0＝（1＋e′2cos2B0）1/2，ν＝（1＋e′2cos2B）1/2，e′为（B0，L0）处椭球第二偏心率，则公式（6）可变为

式（7）即为直接将地面点投影至球面时的长度变形公式。

（2）当地面点距离参考椭球面较远时，可将地面点先归化至相应参考椭球面后再进行球面投影。在这一投影过程中，为减小长度变形，须重新计算新的参考椭球参数，并且须将测区用作首级控制点的国家大地坐标经纬度转换为新参考椭球面上的大地坐标经纬度，再按公式（1）计算球面投影。

目前，在采用参考椭球参数计算时，认为新椭球和国家坐标系相应参考椭球的扁率相等，第一偏心率和第二偏心率与国家坐标系对应的参考椭球的参数相等。即

则新椭球的长半轴计算公式为

式（9）中，e表示国家椭球的第一偏心率，a表示国家椭球长半轴，Bm表示测区中心在国家椭球中的纬度，e′表示国家椭球的第二偏心率，Hm表示测区在国家椭球中的平均大地高（通常用正常高代替）或抵偿面大地高。

其他点在新参考椭球面上的计算同国家椭球，国家控制点在国家参考椭球面上的地理坐标转换到新参考椭球面上的地理坐标计算公式如下：

式（10）和（11）中，B，L和H为国家控制点大地坐标；Δa为国家椭球与新椭球长半轴之差，Δa＝a新－a；M，N分别为参考椭球子午圈、卯酉圈曲率半径。M，N和ΔH的计算公式如下：

取测区中心椭球面标准纬度为B＝33°00′00″，国家椭球参数取WGS–84。采用上述两种方法，将不同高程面的地面点投影至球面时投影长度变形和球面归化长度变形见表2。

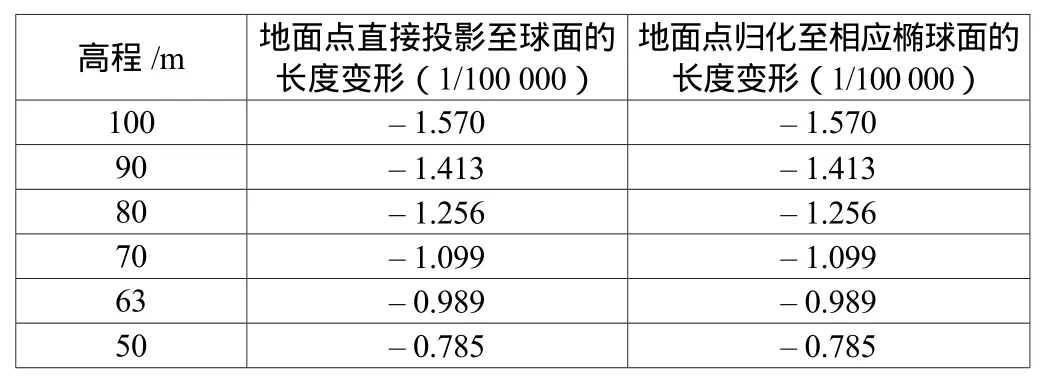
表2 不同高程面上投影长度变形和椭球面归化长度变形

由表2可知，在高度条件不超过100 m时，高程对球面投影长度的变形，以及地面点归化到所参考的椭圆球面的长度变形，可以说是完全相同的。应用双重投影建立抵偿高程面，其高度是63 m（长度变形0.989/10 0000），这与高斯投影的归化高程抵偿面的高程是相同的。

三、斜轴墨卡托投影的长度变形

斜轴墨卡托投影长度变形公式如下：

斜轴墨卡托投影是沿球面与圆柱的切线为投影中线的等角投影，在投影中线上Z＝90°，取地球平均曲率半径R＝6 371 km，斜轴墨卡托投影长度变形随Z角的变化而变化，由式（15）可知，斜轴墨卡托投影长度变形沿投影中线两侧呈对称分布，与投影中线的距离S＝（π/2－Z），由参考椭球面归算到高斯平面的平面坐标长度变形公式如下：

式（16）中，R为测区平均曲率半径，取地球平均曲率半径R＝6 371 km代替；y表示高斯投影横坐标（自然值），即距离投影中央子午线的距离。在距离投影中线或中央子午线不同距离处，斜轴墨卡托投影长度变形与高斯投影长度变形比较结果见表3。

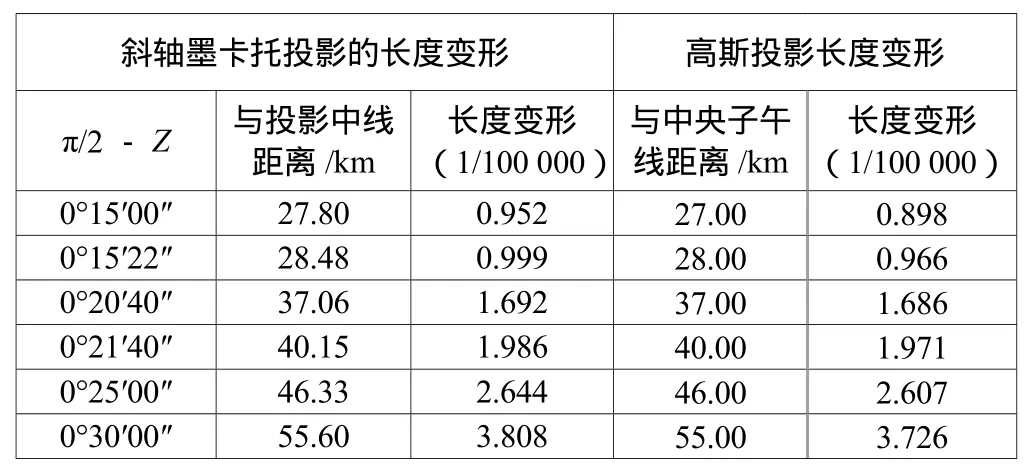
表3 斜轴墨卡托投影和高斯投影长度变形的比较

由表3可知，斜轴墨卡托投影沿投影中线投影，两侧长度变形大小呈对称分布，距离投影中线愈远则长度变形愈大，在长度变形接近1/100 000时，距离投影中线为28 km，投影带宽为56 km。与高斯投影相比较，高斯投影长度变形沿中央子午线两侧呈对称分布，随距离中央子午线距离的增加而增加，如果规定投影长度变形不大于1/100 000，带宽也是56 km，两种投影长度变形的大小基本相等。