卡拉比猜想及其证明
2012-10-24冯晓华
冯晓华 高 策
(山西大学科学技术哲学研究中心,太原030006)
卡拉比猜想及其证明
冯晓华 高 策
(山西大学科学技术哲学研究中心,太原030006)
卡拉比猜想的证明,引出了许多重要结果,对于后来数学和物理的发展做出了基础性贡献。文章依据原始文献,详细考察了卡拉比提出猜想,丘成桐解决卡拉比猜想的工作;同时讨论了卡拉比猜想与凯勒-爱因斯坦度量的密切关系以及丘成桐和奥宾在这两个问题上的工作。
卡拉比 卡拉比猜想 丘成桐 奥宾 凯勒-爱因斯坦度量
数学猜想,尽管被称为合情推理,但仍旧令人不可思议,尤其是提出者本人在猜想上持有极强主见这一现象。卡拉比猜想(Calabi Conjecture)就是其中之一,它是一个关于度量的猜测,度量是刻划空间极其重要的一个特征,人类的生活正是在一个公认的欧氏度量基础上才像现在这样展开的。卡拉比猜想在1954年被卡拉比(E.Calabi,1923~)提出来后,几乎全部知道它的数学家都认为它是错误的,一点意义都没有;连它的最终解决者丘成桐(1949~)一开始也认为它是错误的,而且还给出了很多反例。丘成桐后来说:这个命题太漂亮了,漂亮到令人不可能相信它是对的。[1]就是在这样的情况下,卡拉比始终坚持猜想的正确性。
应该说卡拉比猜想所遇到的丘成桐,与它的提出者具有同样珍贵的执著精神。在卡拉比告诉丘成桐反例推理中的一个错误假设之后,丘成桐在两周之内,夜以继日地思考了几十种方法想要弥补,最终还是意识到卡拉比猜想应该是正确的。由于当时不具备证明这个猜想的技术条件,丘成桐花了3年时间做了大量准备工作,在1976年终于完成了卡拉比猜想的完整证明。[2]从开始证明到最终证明卡拉比猜想,丘成桐花了6年时间,期间的酸甜苦辣,只有自己明了。在证明卡拉比猜想之后,丘成桐用晏小山在《临江仙》中的一句宋词表达了6年中的感受:落花人独立,微雨燕双飞。[1]
丘成桐和卡拉比还有一样相似之处,就是两人对微分几何和微分方程都同等重视,这不是大部分微分几何学家和微分方程家的作风;而这正是卡拉比猜想所具备的特点。
丘成桐对卡拉比猜想的证明,直接与间接地引出了很多结果,导致了许多著名难题的解决,对于后来微分几何、微分方程以及代数几何的发展都做出了基础性贡献。特别地,其中一个重要结果卡-丘流形的存在,在8年之后被应用到弦理论中,演绎了数学与物理学关系史上又一段奇缘。[3]《纽约时报》称,丘成桐在证明卡拉比猜想之后,成为了数学和物理学界一颗耀眼的明星,各种奖项和荣誉滚滚而来。[4]同时卡拉比本人以及卡拉比猜想,在沉默20多年以后,因为丘成桐的工作,也终于闪烁出了他们本来的光芒。
1 卡拉比提出的一个猜想
卡拉比[5]是一位意大利籍美国数学家,在麻省理工读大学期间,他曾获普特南奖,这个奖是为美国和加拿大大学生所设立的数学竞赛奖;1950年他在普林斯顿大学获得了博士学位,他的导师是博赫纳(S.Bochner,1899~1982),一位著名的奥地利-匈牙利籍美国数学家,他的博士论文是《流形的等距复分析嵌入》。[6]在明尼苏达大学期间,卡拉比获得了教授职位;1964年,为了追随在宾夕法尼亚大学已经退休的伟大德国籍美国数学家拉德马赫(H.Rademacher,1892~1969),卡拉比也来到宾夕法尼亚大学数学系,1967年他获任托马斯·斯科特讲座教授,1971~1973年任数学系系主任。[7]1991年因为在微分几何中的工作,他获得了美国数学会斯蒂尔奖,1994年卡拉比退休。
卡拉比主要研究方向是微分几何、偏微分方程及其应用,尤其对凯勒几何(Kähler Geometry或者 Kählerian Geometry)有过很好的研究。[8]单从卡拉比猜想所蕴含的巨大思想就可以看出卡拉比的杰出,只是他的研究常常是那么难以理解,所以他的研究并不是广为数学界所知。卡拉比猜想就是这样的情况,在被丘成桐证明之前的20多年,很多著名几何学家都对它闻所未闻[9]。相对于卡拉比猜想,卡拉比在1953年开创的凯勒流形之间全纯和等距浸入(Holomorphic and Isometric Embeddings of Kähler Manifolds)研究[10]①本是卡拉比以博士论文为基础而写的。的境遇就更差。这同样是一个杰出的研究,但是2倍于卡拉比猜想沉默的时间,仍然不被人们所知,也没被引用过。[11]即使是面对面地讲,卡拉比有时也很难让听众理解自己。据说在20世纪50年代晚期麻省理工学院的一次论坛上,卡拉比做报告,坐在前排的听众之一是传奇与神奇的数学家维纳(N.Wiener,1894~1964)。当时维纳已经60多岁了,和他一贯的习惯一样,一直打瞌睡到演讲结束掌声响起时才醒来。对于报告内容,一些新生在报告开始5分钟后就听不懂了。报告结束后,有个数学家和卡拉比讲了几句话,气氛就陷入了紧张的沉默中。最后还是卡拉比曾在麻省理工学院读书时的老师,60多岁的著名荷兰数学家斯特洛伊克(D.Struik,1894~2000;对于年老的斯特洛伊克,刘钝有过一个珍贵的访谈[12])打破了僵局,他举起手对卡拉比说:能不能说些能听懂的内容。于是卡拉比不得不花了5分钟时间用通俗语言再次讲解了报告的要点,听众才有所满意。[13]
因为这个原因,更应该感谢丘成桐,是他才使人们认识了卡拉比,才有机会去理解卡拉比猜想。这是一个与凯勒几何有关的猜想,这个猜想之所以能够被提出来,首先是源于卡拉比对凯勒几何一直以来的浓厚兴趣;其次是受他的好朋友陈省身(1911~2004)在凯勒几何中工作的启发。陈省身是凯勒几何的创立者之一,他曾发现一种用曲率表示陈类(Chern Class)的方式,特别是陈类中最重要的第一陈类,可以完全被里奇曲率(Ricci Curvature)表示出来。这个发现引出的一个结果是,凯勒几何中里奇曲率的行为受到了第一陈类的约束。针对这个结果,反过来的一个问题是,对于凯勒几何中的里奇曲率,这是否是唯一的约束?就是对这个问题的讨论,卡拉比才会有了他的猜想。①这是2011年9月3日丘成桐教授在通信中给出的解释。
1.1 首次提出猜想
卡拉比首次提出他的猜想是在对所有典范类(或第一陈类)为零的紧凯勒流形(Kähler Manifold)进行分类的工作中。为了完成分类,卡拉比首先需要知道典范类为零紧凯勒流形的性质,依据这些性质才能进行分类。在获取典范类为零紧凯勒流形性质的时候,出现一个问题,就是旧有典范类的定义(即任何非零亚纯n次微分约数的同调类)不能够判断是否可以总是在所有流形中找到这个宽类的一个非平凡亚纯n次微分,所以不适合用于对紧复流形的推广。而陈省身[14]已经提出一个交错的定义,可以允许这种推广;所以卡拉比引入陈省身的定义,重新定义并引进了一些概念和一些性质,从而改进了旧有典范类的定义。这样,卡拉比就得到了紧凯勒流形的一些拓扑和调和的性质。其中一个重要性质,就是他的猜想,即:
Mn是一个紧复流形,在其上允许具有主形式ω和里奇形式Σ的无限可微凯勒度量,如果Σ'是(1,1)型的任意闭实值无限可微形式,且上同调于Σ,那么存在唯一的一个凯勒度量,它具有主形式ω',上同调于ω,且里奇形式与Σ'相等。这个度量总是无限可微的;如果Σ'是解析的,它也是实解析的。
对于这个处于猜想状态的性质,卡拉比认为,虽然目前还无法被完全证明,但是出于一种综合的、直觉上的原因,把这个真理以命题的形式写出来是正当的,况且他对如何证明这个命题还能提出一些富于启发性的建议。
卡拉比认为,要证明这个猜想需要分两步:
第一步,证明猜想中所说的具有指定里奇形式凯勒度量的唯一性;
第二步,证明这个凯勒度量的存在性。
其中唯一性已经有了严格证明;对于存在性,卡拉比虽然无法给出严格证明,但他有一套切实可行的详细证明计划。首先卡拉比已经明确存在性的证明,依赖于一个积分微分方程解的存在性假定;接着要做的事可以分两步操作:
(1)获得这个积分微分方程。对此卡拉比证明了属于相同主类不同度量的两个主形式如果不同,那么它们相应的凯勒形式也是不同的。这是一个重要的结论,有了它就能够给出实参数[0,1]上里奇形式的连续系统Σ(t)和相应的主形式ω(t)对于t的导数之间的关系这就是与凯勒度量存在性证明相关的积分可微方程。
(2)求解这个积分可微方程。考虑函数∂∑(t)/∂t可微的充分条件,方程就会有解ω(t),它的初始值由任意无限可微凯勒度量的主形式ω(0)给出。特别的,如果使初始值与命题中假定的凯勒度量对应,选择∂∑(t)/∂t为两个不同里奇形式的差Σ'-Σ,方程的解是ω(t);那么ω(0)=ω就给出了凯勒度量的主形式,它的里奇形式满足Σ(t)=Σ +t(Σ'-Σ),当t=1的时候,具有指定里奇形式Σ'的凯勒度量就是方程的解。
为了严格上述讨论,首先需要考虑的是,由于t是变量,所以方程保持了它的椭圆性质。因为这个原因,方程的解ω(t)就t而言是局部连续的;但是对于求解ω(t)的t的区间是否是无界的,卡拉比无法给出答案,而这正是证明他的猜想的一个基本缺口,这个缺口使得后面的分类工作建立在一个猜想基础上:即紧凯勒流形允许凯勒度量,它具有任意指定的正可微体积元。
跳过这个缺口,卡拉比指出对于∂∑/∂t=Σ'-Σ(0),要证明方程解ω(t)的存在性,可以通过求ω(t)的二阶导数的值和求ω(t)以及ω(t)的一阶导数的优先估计,然后应用折线逼近的柯西-佩亚诺方法求解。最终,卡拉比无法严格求解这个方程,但是经过上述对方程求解思路的讨论,起码使这个猜想看起来是可能的。
在所有这些性质的基础上,对典范类为零的紧凯勒流形进行分类就成为可能。首先,卡拉比讨论了两类典范类为零的紧凯勒流形:一类是由n维复环面给出的,另一类是由非奇异超曲面给出的。其中卡拉比给出了描述第一类凯勒流形性质的一个定理,在证明这个定理的一开始,卡拉比就使用了他的猜想,将给定的凯勒度量替换成具有相同主类的另一个里奇张量等于零的新度量,这个新度量是唯一的且实解析的,之后的证明都是在这个新度量上展开的。证明完这个定理之后,卡拉比还给出一个定理,作为对第一个定理的一种新的解释,以便更加有助于描述第一类特殊凯勒流形的结构。运用这些结果,卡拉比完成了对所有典范类为零的紧凯勒流形的分类。
1954年4月8~10日在普林斯顿大学范恩会堂(Fine Hall,数学系所在大楼)为庆祝数学家莱夫谢茨(S.Lefschetz,1884~1972)70岁生日而举办的代数、几何和拓扑会议上,卡拉比以“典范类为零的凯勒流形”[15]为题汇报了上述工作,并于1957年被刊载在该会议论文集上。这个报告被看作是卡拉比在公开场合首次对猜想的表述。
尽管文章已经发表出来了,但是由于卡拉比对紧凯勒流形的分类工作是建立在一个猜想之上,所以这个分类工作还不能算真正完成(从严格意义上说,只有在丘成桐完全证明卡拉比猜想之后,这个分类工作才算彻底完成)。正是因为这一点,这个原本只是关于紧凯勒流形一个性质的猜想,很快成为令卡拉比无比重视的一个问题,于是在同一年国际数学家大会上,卡拉比专门讨论了这个猜想,希望引起人们的注意,来实现对猜想的完整证明。
1.2 对猜想的专门讨论
1954年9月2~9日在荷兰阿姆斯特丹国际数学家大会上,卡拉比做了一个简短的报告《凯勒度量空间》[16],专门讨论在《典范类为零的凯勒流形》报告中提出的猜想。两次报告相距不到5个月,在这段时间中,卡拉比为猜想做了两个工作:
首先,更加清晰地阐述猜想。
卡拉比发现如果事先给出一个有关凯勒度量空间的性质,人们理解猜想就会容易得多,这个性质就是:在紧复流形Mn上,假定至少可以允许存在一个具有里奇形式Σ的凯勒度量gαβ*,度量的主类是ω;那么对于Mn中所有具有上述主类的凯勒度量的空间Ω,存在一个事实:空间Ω中任意的凯勒度量的里奇形式Σ是一个闭实(1,1)型,并且它的上同调类等于2πC(1)。
对于这个事实,人们反过来自然会问的一个问题是:对于任意闭实(1,1)型,什么样的才能成为Mn上凯勒度量的里奇形式,[17]卡拉比猜想就是在回答这个问题。虽然卡拉比没有明确指出这一点,但他重新陈述猜想的内容却体现了这一点:
给定Mn中(1,1)型的任意实闭无穷次可微外形式Σ,且上同调于2πC(1),那么在Ω中一定存在唯一的凯勒度量,它的里奇形式等于Σ。其次,进一步讨论证明猜想的思路。
在从不同角度赋予猜想更加清晰的数学意义之后,卡拉比重新给出了证明猜想的思路,还是分两步:第一步证明猜想中凯勒度量的存在性,主要是通过在各种型的相同线性空间中的可微参数化弧,其中要涉及Ω中具有Σ的度量的里奇形式,来构建Ω中一个相应的参数化路径;第二步证明猜想中凯勒度量的唯一性,并且要它的终点独立于路径。
在这种证明思路的基础上,卡拉比讨论了一个特例。在给定Mn某些限制性质的情况下,Ω中存在一个度量,它最小化成(Σ,Σ),除了Mn的解析变换,这个度量是唯一的,而且通过这个性质的刻画,标量曲率是常量。其中,标量曲率是常量表明空间是爱因斯坦的,度量是爱因斯坦的[18]。
对于卡拉比来说,这些证明思路是多么清楚与流畅,可就是差些什么,使得整个证明过程无法连贯写出来。这种只差一步的感觉是令人沮丧的。更加沮丧的是,几乎没有数学家相信这个猜想是对的。不过,卡拉比无需对此沮丧,因为貌似的一小步,实则蕴含了很多数学内容,而这些数学内容在当时还未被写出来,丘成桐花了3年时间才将这些空缺的数学内容填补上,沿着卡拉比提出的思路,实现了猜想的完整证明。
2 丘成桐对卡拉比猜想的证明
要讨论丘成桐对卡拉比猜想的证明,是不能直入主题的,因为丘成桐本人就没这样做。只有重新回顾丘成桐所走的道路,才能真正理解这位数学家和这个猜想在6年间所建立的深厚情感,才能深刻理解丘成桐对卡拉比的崇敬之情。
2.1 证明猜想的曲折经历
陈省身比卡拉比年长12岁,两人研究领域互有交叉,经常一起参加一些讨论班和会议[19]。作为陈省身的学生,丘成桐对卡拉比的研究工作自然比别人接触要多。在伯克利的第一年(1969~1970),丘成桐[20]就曾推广和改进了卡拉比[21]关于紧致平坦黎曼流形的工作。在伯克利的第二年,丘成桐就开始考虑凯勒几何中的卡拉比猜想了[22],不过当时他的这个选择,并没有被看好。因为几乎所有人甚至包括丘成桐的导师陈省身都认为这个猜想是错误的;不仅如此,陈省身还认为这个研究方向的意义不大。这些意见并没有影响丘成桐求解卡拉比猜想的决心,他固执地认为对卡拉比猜想总要找出一个水落石出的答案。能这样做,是不容易的。其中有一个重要的学术原因,就是当时丘成桐极其钟爱里奇曲率,他认为里奇曲率对于理解宏观几何是特别重要的。但是直到看到卡拉比在1954年关于里奇曲率猜想的文章时,他才第一次找到了研究里奇曲率的切入点。[23]既然如此,又如何能放弃呢。
早在20世纪60年代晚期,一些怀疑卡拉比猜想正确性的人曾使用齐杰(J.Cheeger,1943~)和格罗莫尔(D.Gromoll,1938~2008)[24]的还原理论来构造卡拉比猜想的反例,都没有成功。丘成桐一开始也是沿袭了前人的这种研究方法与观点,试图证明卡拉比猜想是错的,最终都以失败告终。从伯克利毕业后,丘成桐到了拓扑学中心普林斯顿高等研究院任职(1971~1972),在那里丘成桐仍旧对卡拉比猜想很有兴趣[9],曾对卡拉比猜想构造过一系列的反例,并在私下里解释他的构造,或在会议上做一个非正式的演讲,但是最后在他的构造里总能找出漏洞。[2]
1973年暑假,在微分几何中心纽约州立大学石溪(Stony Brook)分校数学系作助理教授的丘成桐参加了美国数学会在斯坦福大学举行的微分几何大会,年轻的丘成桐当时在微分几何领域已经处于领先水平,他在会上作了3个学术报告。在这次大会上,物理学家杰拉奇(R.Geroch)向数学家们讲演了广义相对论,解说了正质量猜测(即爱因斯坦猜想),并牵扯出了与之相关的卡拉比猜想。[25]卡拉比猜想在这种场合的再次出现,激发了丘成桐解决它的强烈愿望。就在会议期间,他使用还原理论并采用反证法来考察卡拉比猜想。在假定猜想正确的情形下,他得到了一个分裂理论:每一个里奇曲率等于零的紧凯勒流形,能够被圆环面和具有里奇平坦凯勒度量的单连通流形的度量积所覆盖。[26]使用这个理论,他获得了卡拉比猜想的一个反例,由此证明卡拉比猜想是错误的。他把得出的结果告诉了几个朋友,朋友们要求他在大会上把他的工作讲出来。于是丘成桐就在大会上当众讨论了他的想法并宣布了他的结果,没有人表示反对。
但有一个人存疑,他就是一直坚信猜想正确的卡拉比本人。会后他花2个月时间仔细分析了丘成桐的论证,发现在推理中丘成桐错误的假定:具有大量非负反典范约数的流形允许点态非负的第一陈类。[26]卡拉比写信将此告诉了丘成桐,丘成桐说这是他研究生涯中最痛苦的经历了,虽然当时只是在大会上宣布了他的想法和结果,并没有将此成文发表,但是这也足以使名誉因为所犯的错误毁于一旦。他说那些日子辗转反侧,不能成眠,不断反复考察每一步推理,不断尝试各种证明,想了很多办法来弥补这个错误假定,但是每次都是眼看快要成功的时候,却在最后一个很小的地方推不下去,这种状况一直持续了2个星期。在经历几十次证明的失败后,丘成桐发现,在为卡拉比猜想寻找反例的过程中,首先是假设卡拉比猜想是对的,然后考虑其后果。而卡拉比的来信表明这个反证法是行不通的,他意识到问题反过来是对的。于是他向卡拉比写信,承认反例是错的,根本没有办法弥补,他要反过来证明猜想的正确性。不仅如此,丘成桐还撤销了他在斯坦福大学会议上所做的有关猜想反例的报告,开始转变思路着手证明猜想的正确性。[2]
很快,丘成桐就将卡拉比在“典范类为零的凯勒流形”中提到的与猜想密切相关的积分可微方程进一步明确成一个复蒙日-安培方程。蒙日-安培方程是一类很古老的二次非线性偏微分方程,它经常出现在微分几何里。巧合的是,这个方程中的蒙日(G.Monge,1746~1818),也是18世纪少有的对几何和分析予以同等重视的数学家。[27]
丘成桐要求解的这个复蒙日-安培方程是一个很难的非线性偏微分方程,他花了将近3年的时间,做了大量准备工作:和好友郑绍远(与丘成桐同为陈省身的学生)合作研究蒙日-安培方程、仿射几何和极大曲面等相关问题;和舍恩(R.Schoen,丘成桐的第一个博士生)合作研究调和映照;和舍恩、西蒙(L.Simon,1945~;在斯坦福大学的澳大利亚数学家,曾和丘成桐共同指导舍恩)研究极小曲面。[2]通过这些准备工作,丘成桐发展了强有力的偏微分方程技巧,使用先验估计方法,在1976年6月终于求解了这个非线性复蒙日-安培方程,从而给出了卡拉比猜想的完整证明。
尽管说一个问题的解决不会只限定在一个人身上,但对于卡拉比猜想的证明,是有丘成桐本人的特质在里面的。丘成桐在伯克利刚学几何学的时候,流行的是度量几何,所有工具都是从三角比较定理来的;作为一名年轻的研究生,丘成桐通过大量的听课与习题,感觉到微分几何的工具很多是从微分方程方面来的,所以他觉得当时研究几何的做法对几何的刻画不够深刻。于是本来就乐此不疲听各种课的丘成桐去跟近代偏微分方程的奠基者莫里(C.Morrey,1907~1984)学习了微分方程,巧的是莫里常常用微分方程来做一些微分几何的问题,于是丘成桐也和几个朋友以及学生做一系列用微分方程做工具的几何研究。对于莫里的研究,当时的微分几何学家并不是很清楚,因为在当时做几何的人有一个共同的想法,他们认为微分方程跟微分几何无关,而且认为微分方程不是主流,所以做微分几何的一般不去注意微分方程。[28]如果说在伯克利,对微分方程的接触使丘成桐萌生了研究微分几何的某种想法,那么在斯坦福大学,这种在微分几何上的新想法则有机会得到进一步发展。尤其在斯坦福大学期间证明卡拉比猜想之后,丘成桐开始响亮地提出对于研究微分几何的新想法。1978年8月15~28日,在芬兰首都赫尔辛基举行的18届国际数学家大会上,29岁的丘成桐作为重要受邀报告者作了题为“偏微分方程在几何中的作用”[29]的报告。1982年3月31日~4月2日,在34届英国数学研讨会上,丘成桐作了题为“微分几何中的非线性方程”的报告,这次研讨会全体出席的大会报告只有3个,丘成桐的报告就属于其中之一。[30]正是这个微分几何学家对微分方程重要性的深刻认识,才使他能花3年工夫求解与卡拉比猜想有关的复蒙日-安培方程。
非线性复蒙日-安培方程的求解,直接表明卡拉比猜想的可证性。对于沉浸其中达6年之久的丘成桐,迫切想要与更多的人分享这个结果。在受美国斯隆基金资助的情况下,丘成桐将思路系统整理成两页,于1977年1月31日由陈省身将其递交到世界著名的《美国科学院院刊》,1977年5月便被迅速刊载出来,题为“卡拉比猜想以及代数几何中的一些新结果”[31],其中丘成桐对卡拉比在猜想什么,卡拉比解决了什么问题,遗留了什么问题,作了简洁清楚的解释。有理由说丘成桐是对卡拉比猜想理解最深刻的人,他的解释是理解卡拉比猜想最好的陈述。在此基础上,丘成桐给出一个定理,首次宣称对卡拉比猜想的证明。1977年6月,丘成桐在访问纽约大学数学科学科朗研究院的时候终于完成了长达73页的卡拉比猜想详细完整的证明,1978年5月被刊载出来,题为“关于紧凯勒流形的里奇曲率和复蒙日-安培方程,Ⅰ”[32],直接醒目地将证明卡拉比猜想的核心都体现在了一起,并且文中对卡拉比猜想有了更加深刻简明地阐释。
2.2证明猜想的数学过程
在讨论丘成桐如何证明卡拉比猜想之前,还需要交代一下他对卡拉比猜想的理解。卡拉比猜想到底在说什么,找出卡拉比的两篇论文读一下,都未必清楚,这也是它一度被认为毫无意义的原因之一。对于这个猜想,丘成桐在1977年5月和1978年5月两篇论文中,分别做过两次不同表述,这表明就是到最后,丘成桐对卡拉比猜想的理解都在不断升华。
在第二次表述中,丘成桐先将卡拉比在“凯勒度量空间”一开始给出的凯勒度量空间的性质,描述成这样一件事:(1,1)型能够成为某个凯勒度量里奇形式的必要条件是它必须是闭的,并且它的上同调类必须表示M的第一陈类;在此基础上,丘成桐提出卡拉比所猜想的就是:上述必要条件也是充分条件。
理解清楚卡拉比猜想之后,丘成桐依循卡拉比提出的证明思路,开始构造与卡拉比猜想等价的非线性偏微分方程。主要有两步:
第一步:从上述必要条件出发构造方程。如果(1,1)型是闭的并且是M的第一陈类,那么它可以成为某个凯勒度量的里奇形式;再根据已知,能够找到M上的一个光滑函数F,就会有一个方程(0.1)经过两次等价变换,最后方程(0.1)等价变换为方程(0.4)
这样,丘成桐就找到了与卡拉比猜想等价的方程(0.4)。对于方程(0.4),卡拉比已经证明了它的解的唯一性;并且还证明了方程(0.4)等式右边非常接近于一个常量时,方程(0.4)存在一个光滑解。遗留的问题是:在没有任何限制条件下,证明方程(0.4)解的存在性。丘成桐全面讨论了方程(0.4),不仅解决了卡拉比遗留的问题;同时还推广了卡拉比猜想,将方程(0.4)推广到了更一般的情形复蒙日-安培方程(0.6):
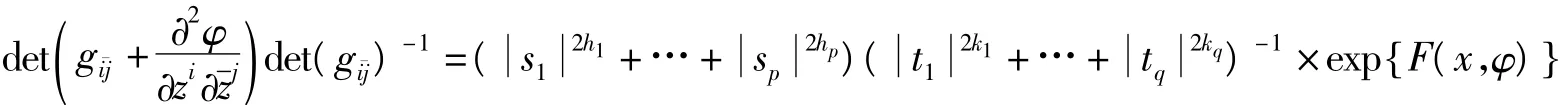
只是,这种推广存在一个问题,就是与方程(0.4)相比,方程(0.6)相当难解。怎么办呢?丘成桐发现当方程(0.6)的右边特殊成形式exp{ φ+F(x)}时,方程(0.6)不仅比方程(0.4)容易求解,而且还能够简化成具有丰富典范线丛的紧凯勒流形上典范凯勒-爱因斯坦度量的存在性和唯一性问题。受此启发,丘成桐从方程(0.6)的特殊情况开始,通过使用连续性方法,最后求解了方程(0.6)。
求解方程(0.4)和(0.6)的过程说起来简单,做起来是相当复杂的,尤其是其中所使用的大量先验估计,有的文字评价其为眼花缭乱与惊心动魄。
第一步,丘成桐为证明建立一套术语。
第二步,丘成桐就迅速开始了他高超的先验估计技术。在C=1的情况下对方程(0.4)的解φ进行二阶估计和三阶估计。具体的数学过程是相当技术性的,丘成桐首先对方程连续作了两次微分,并且引进正规化拉普拉斯算子的表示,得到一个新的方程。为了便于计算,他使用了一套新的坐标系,引进了13个常量,应用了一些性质,进行了13次估计,使用了归纳假设,另外还在测地球上使用了很多假设讨论φ解。进行了几乎14页的运算,丘成桐终于给出了方程φ解的二阶估计。为了获得方程φ解的三阶估计,丘成桐考虑了卡拉比[33]在 1958 年曾研究过的函数 S= Σ g'i¯rg'¯jsg'k¯tφi¯jkφ¯rs¯t的拉普拉斯算子,通过多次估值之后,得到了φ解的三阶估计。
第三步,丘成桐开始目标方程的求解,证明卡拉比猜想。在上述φ解二阶和三阶估计的基础上,丘成桐找到了一个φ解。根据这个结果,可以找到卡拉比猜想所等价方程(0.4)的一个光滑φ解,这样卡拉比所猜想的凯勒度量的存在性就得到了证明。
第四步,丘成桐讨论了方程(0.6)。这个方程无法直接求解,丘成桐采取了从特殊到一般的方法,先求解这个方程右边退化成4种特殊情形的方程,这个过程还给出了许多好的数学结果。
第二种情形是方程(0.6)右边退化为exp{ F(x,φ)}。丘成桐首先证明了这个方程解的唯一性,接着使用迭代法,通过大量技术性很强的估值、计算,使用了大量常量,最终求解了这个方程。这个方程的求解,同时引出了一个结果:在具有丰富典范线丛的凯勒流形上,存在唯一的凯勒-爱因斯坦度量。
完成上述4种特殊情形的求解工作之后,方程(0.6)就很好求解了,丘成桐最终求解了这个一般的复蒙日-安培方程。至此对于与卡拉比猜想等价的方程(0.4)以及其推广后更一般的方程(0.6),丘成桐都进行了全面的研究,不仅完美地完成了卡拉比猜想的首次完整证明,而且还首次推广了卡拉比猜想。这篇论文可以说将丘成桐在数学上的才华展露无遗。
丘成桐解决卡拉比猜想之后,在论文还没有正式发表出来之前,就立刻受到卡拉比邀请到宾夕法尼亚大学做报告,听众中有宾夕法尼亚大学的著名数学家卡兹丹(J.L.Kazdan),他的主要研究领域也是微分几何和偏微分方程。几个月之后,卡兹丹[34]进一步简化了丘成桐在二维情况下卡拉比猜想的证明(这个简化与丘成桐的文章刊载在同一期上)。得知此事,法国朱西厄(Jussieu)数学中心的奥宾(T.Aubin,1942~2009),邀请卡兹丹介绍了丘成桐在二维情况下对卡拉比猜想的证明以及卡兹丹本人的简化。1977年年底,奥宾和博规农(J.P.Bourguignon,1947~)在布尔巴基讨论班正式介绍了丘成桐的工作,并且二人独立地将丘成桐在二维情况下对卡拉比猜想的证明推广到了高维。[32]
丘成桐在完成卡拉比猜想证明以后的心情,不是仅仅用激动、欣喜这些词语能够表达的。六年的时间,那是一种成长,那份心情也深深地镌刻在了这个研究中一直给予他鼓励的人中:卡拉比、陈省身、郑绍远、小林昭七(S.Kobayashi,1932~)、科恩(J.J.Kohn,1932~)、劳森(B.Lawson)、尼伦伯格(L.Nirenberg,1925~)和萧荫堂(1943~)。陈省身就丘成桐的论文专门组织了报告会,丘成桐认为这对论文在表述方面的改进有重要意义,无论怎样表达陈省身的帮助与鼓励都毫不夸张。丘成桐认为和郑绍远合作的文章对论文有非常明确的影响。丘成桐认为和尼伦伯格就复蒙日-安培方程进行过多次很有帮助的交谈,特别是有关卡拉比计算的复类比。丘成桐将该研究献给了他的母亲梁若琳,并以此纪念他的父亲丘镇英。他说父亲生前研究领域包括哲学、经济和中国文化,父亲的深刻洞察力对他有很大的影响。父亲早早去世了,母亲挑起了贫穷的家庭重担,抚养和教育了7个孩子。丘成桐说没有父母长久以来的教育,他不可能成为一个数学家。[32]
3 卡拉比猜想与凯勒-爱因斯坦度量的密切关系
解决卡拉比猜想的荣誉毫无争议的属于丘成桐,但是在20世纪70年代还有一个比丘成桐大7岁的年轻人,他在卡拉比猜想上的工作需要提及,即法国数学家奥宾。奥宾生前就职于法国朱西厄数学中心,1990年当选法国科学院通讯院士,2003年成为法国科学院院士,主要研究方向是微分几何和非线性偏微分方程,他被称为法国几何分析的一个重要先驱,他广为人知的两个研究是山边问题[35]和卡拉比猜想。[36]
对于奥宾在卡拉比猜想上的工作,主要体现在3篇论文中:一篇是1970年的《黎曼度量和曲率》[37],有42页;一篇是1976年的《紧凯勒流形的复蒙日-安培方程》[38],有 3 页;还有一篇是与1976年论文同名的1978年的论文[39],这个论文主要是对1976年论文的详细论述,有33页。
在1970年的论文中,奥宾在第一陈类为负,且假定凯勒流形具有非负全纯双截曲率情况下,求解了类似丘成桐的右边为exp(F)的复蒙日-安培方程[31];在1976年的论文中,奥宾充分论证了第一陈类为负的情况,并且在第一陈类为正的情况下,求解了类似丘成桐的右边为exp(cφ+F)的复蒙日-安培方程[31];从而给出了卡拉比猜想的一个部分证明。在1978年的论文中,奥宾对1976年论文进行了更加详细的论述[36],论文页数由3页变为33页。
阿布德塞拉姆(A.B.Abdesselem)[36]在纪念奥宾的文字中指出:奥宾最后几乎完全证明了卡拉比猜想。在丘成桐之前,奥宾的这些工作确实是一个巨大的贡献,但是数学界并未因此而震惊。丘成桐认为原因有两个:一是奥宾是在假定凯勒流形具有非负全纯双截曲率的情况下,给出的卡拉比猜想的证明,这种具有非负全纯双截曲率的凯勒流形的类是相当有限制性的;二是在证明中,奥宾使用了变分法,这种方法不是很容易理解的。[32]就是奥宾([40],139页)本人在后来的著作中也提到了这一点,他说连续性方法更简单(这是丘成桐使用的方法);而且在讨论卡拉比猜想时,他使用了连续性方法,而不是变分法。
后人常常将奥宾与卡拉比猜想联系在一起讨论;奥宾本人则更倾向于将他的这些工作与凯勒-爱因斯坦度量联系起来,在他后来的文字中可以看到这一点。
从这个角度,奥宾的上述工作又可以阐述为:在1970年的论文中,奥宾首次研究了紧凯勒流形上凯勒-爱因斯坦度量存在性问题,并将其转化成奥宾方程logM(φ)=-λφ+f的求解问题。在1976年的论文中,奥宾证明了第一陈类为负的紧凯勒流形上存在凯勒-爱因斯坦度量。[41]对于奥宾的工作,博规农[42,43]做了很好的解释。([44],251 页)
凯勒-爱因斯坦度量是里奇形式与凯勒形式成比例的度量,也就是要求复流形上的度量不仅是凯勒度量,而且也是爱因斯坦度量。其中爱因斯坦度量是里奇形式与度量形式成比例的度量,之所以称为爱因斯坦度量,是为了纪念爱因斯坦,因为这个条件也相当于说这个度量是真空爱因斯坦方程的一个解。允许爱因斯坦度量的黎曼流形称作爱因斯坦流形;这类流形与很多重要论题有联系,包括杨-米尔斯理论。在已知的爱因斯坦流形的例子中,非常好的一类就是凯勒的。([45],96~97页)
紧凯勒流形上凯勒-爱因斯坦度量存在性问题与卡拉比猜想有密切关系,奥宾([40],139~156页;[44],251~288页)、贝斯(A.L.Besse)([45],318~339页)、莫罗亚努(A.Moroianu,1971~)[46]等人的著作都有专门章节论述,总的来说,有四个方面:
(1)从二者提出问题的角度分析。凯勒-爱因斯坦度量存在性问题是:已知紧凯勒流形上存在凯勒-爱因斯坦度量的必要条件是第一陈类为负、零和正;那么这是否也是充分条件。换句话说就是,紧凯勒流形上是否存在凯勒-爱因斯坦度量。卡拉比猜想的问题是:已知紧凯勒流形上每一个(1,1)型成为其上某些凯勒度量里奇形式的必要条件是这些形式表示第一陈类;那么这是否也是充分条件。换句话说就是,紧凯勒流形上每一个表示第一陈类的形式是否都是其上某些凯勒度量的里奇形式。([44],254~255页)
(2)从二者所等价的方程分析。凯勒-爱因斯坦度量存在性问题等价于求解奥宾方程,当λ为负、零或正时,这个方程的解分别给出第一陈类为负、零和正的凯勒流形上的凯勒-爱因斯坦度量。特别的当λ=0的时候,这个问题就是卡拉比猜想:即第一陈类为零的紧凯勒流形上,允许里奇平坦凯勒度量。[41]后来卡拉比曾通过口头交流,将猜想推广成第一陈类是负定的且爱因斯坦度量具有符号-1(即λ=-1)。([45],8页)到丘成桐的时候,卡拉比猜想可以分为三种情况,即第一陈类为负、零或正。在这三种情况下,凯勒-爱因斯坦度量的存在性问题就等价于求解右边为exp(cφ+F)的复蒙日-安培方程。[31]
(3)从卡拉比、丘成桐和奥宾的论文分析。本文前边有关卡拉比和丘成桐论文的论述是侧重于卡拉比猜想的,而事实上,在他们的论文中都可以看到有关凯勒-爱因斯坦度量的论述。卡拉比在《凯勒度量空间》一文中,实际上也隐含着猜想了凯勒流形上存在凯勒-爱因斯坦度量,其中凯勒流形的第一陈类为负、零和正,并且它不允许任何全纯向量场。[31]丘成桐在《卡拉比猜想以及代数几何中的一些新结果》一文中给出凯勒-爱因斯坦度量这个名称以及对其的阐释,在《关于紧凯勒流形的里奇曲率和复蒙日-安培方程,Ⅰ》中,定理5就给出了第一陈类为负时的凯勒-爱因斯坦度量。奥宾在《黎曼度量和曲率》一文中就明确提到了爱因斯坦度量,该文第十节就是有关“爱因斯坦度量存在性的充分条件”。
(4)从卡拉比、丘成桐和奥宾论文给出的结论分析。1976年,丘成桐在给出卡拉比猜想完整证明的同时,也证明了第一陈类为负和零的情况下,紧凯勒流形上凯勒-爱因斯坦度量的存在性。丘成桐在卡拉比猜想上的工作与卡拉比的工作一起被称为卡-丘定理,这是一个有关卡拉比猜想的定理。丘成桐和奥宾在凯勒-爱因斯坦度量存在性上的工作与卡拉比的工作一起被称为奥宾-卡-丘定理,这是有关凯勒-爱因斯坦度量存在性的定理;进一步,第一陈类为零情况下的凯勒-爱因斯坦度量被称为卡-丘度量,第一陈类为负情况下的凯勒-爱因斯坦度量称为奥宾-卡-丘度量。([45],322~323页)
部分的因为奥宾和丘成桐的这些工作,再次引发了对爱因斯坦流形的研究。1979年9月,在法国的埃斯帕利永就召开了关于爱因斯坦流形的讨论会。([45],5页)
尽管卡拉比猜想与凯勒流形上凯勒-爱因斯坦度量存在性问题密切相关,但二者毕竟是两个独立的问题。卡拉比猜想在1976年由于丘成桐的工作,已告完全解决;而凯勒流形上凯勒-爱因斯坦度量存在性问题,当时奥宾和丘成桐解决了第一陈类为负、丘成桐解决了第一陈类为零的情形,对于第一陈类为正的情形,至今仍未解决。不过对于数学和物理,第一陈类为正情形的重要性远远不及前两种情形。后来,丘成桐[47,48]曾提出一个稳定性原则来研究这个问题,这个想法被称为丘成桐猜想。对此丘成桐的学生们,包括田刚(1958~)[49—51],作了诸多努力,给出了一些有意义的结果。最近,在这个问题上,唐纳森(S.K.Donaldson,1957 ~ )[52—54]和陈秀雄[55]又给出了一些进展。①对于第一陈类为正情形的了解,来自2011年5月14日与丘成桐教授和季理真教授的通信。
致 谢这个主题的文章能够写出来,要感谢很多人的帮助,他们给了我勇气、很多重要文献以及修改建议。谢谢您们:徐浩(Hao Xu)、Chen-Yu Chi、Rui-Fang Song和李逸(Yi Li)博士,李文林研究员,丘成桐(Shing-Tung Yau)、季理真(Li-Zhen Ji)、刘克峰(Ke-Feng Liu)和陶布斯(C.Taubes)教授。
1 在“卡拉比猜想”时空里神游—华人数学家丘成桐访谈录[J].百年潮,2007,(3):22~27.
2 季理真,刘克峰.丘成桐—站在数学之巅的科学巨匠[M]∥刘克峰,季理真.丘成桐的数学人生.杭州:浙江大学出版社,2006.135~136.
3 冯晓华,高策.弦理论与卡-丘流行的结合[J].科学技术哲学研究,2011,(4):68~77.
4 Scientist at Work:Shing-Tung Yau The Emperor of Math[N].NYTIMES,2006-10-22.
5 Eugenio Calabi[DB/OL].[2010-10-12].http:∥www.worldlingo.com/ma/enwiki/en/Eugenio_Calabi/1.
6 Eugenio Calabi.[DB/OL].[2010-10-12]http:∥genealogy.math.ndsu.nodak.edu/id.php?id=8111.
7 Department Chairs.Department of Mathematics.University of Pennsylvania.[DB/OL].[2010-10-25].http:∥www.math.upenn.edu/History/dept_chairs.html.
8 Bourguignon J P.Eugenio Calabi and Kähler metrics[M]∥Manifolds and Geometry,Proceedings of the Symposium on Mathematics.Cambridge:Cambridge Univ.Press,1996.61 ~85.
9 郑绍远.我的老朋友丘成桐[M]∥刘克峰,季理真.丘成桐的数学人生.杭州:浙江大学出版社,2006.封页.
10 Calabi E.Isometric imbeddings of complex manifolds[J].Ann.of Math,1953,58(2):1 ~23.
11 Berger M.Encounter with a geometer:Eugenio Calabi[M]∥Manifolds and Geometry,Proceedings of the Symposium on Mathematics.Cambridge:Cambridge Univ.Press,1996.20 ~60.
12 刘钝.数学、历史和马克思主义——介绍美国数学史家 D.J.斯特洛伊克[J].科学技术与辩证法,2002,(2):72 ~76.
13 Rota G C.Ten lessons I wish had been taught[J].Notices of AMS,1997,44(1):22 ~25.
14 Chern S S.Characteristic classes of Hermitian manifolds[J].Ann.Math,1946,47(2):85 ~121.
15 Calabi E.On Kahler manifolds with vanishing canonical class[M].∥Fox R H,Spencer D C,Tucker A W.Algebraic Geometry and Topology:a Symposium in Honor of S.Lefschetz.Princeton:Princeton University Press,1957.78 ~89.
16 Calabi E.The space of Kähler metrics[M].∥Erven P,Noordhoff N V.Proceedings of the International Congress of Mathematicians(Amsterdam,1954).Vol.2.Amsterdam:North-Holland,1957.206~207.
17 Joyce D D.Compact Manifolds with Special Holonomy[M].Oxford:Oxford University Press,2004.98.
18 Kobayashi S.Hypersurfaces of complex projective space with constant scalar curvature[J],J.Differential Geometry,1967,1(3 ~4):369 ~370.
19 On the Photo:Chern Shiing-Shen.Oberwolfach Photo Collection.[DB/OL].[2010-11-02].http:∥owpdb.mfo.de/detail?photo_id=7484.
20 Yau S T.Compact flat Riemannian manifolds[J].J.Diff.Geom,1972,6(3):395 ~402.
21 Calabi E.Closed locally Euclidean 4-dimensional manifolds[J].Bull.Amer.Math.Soc,1957,63(2):135.
22 刘克峰,徐浩.丘成桐先生学术成就[M]∥刘克峰,季理真.丘成桐的数学人生.杭州:浙江大学出版社,2006.163.
23 丘成桐.研学之乐[N].光明日报,2011-01-10.
24 Cheeger J,Gromoll D.The splitting theorem for manifolds of nonnegative Ricci curvature[J].J.Differential Geometry,1971,6(1):119~128.
25 丘成桐——数学界的“凯撒大帝”[N].中国教育报,2009-10-23.
26 Yau S T.Calabi-YauManifold.2009[DB/OL].[2010-11-07].http:∥www.scholarpedia.org/article/Calabi-Yau_manifold.
27 李文林.数学史教程[M].北京:高等教育出版社,2001.198.
28 丘成桐.我研究数学的经验[M]∥刘克峰,季理真.丘成桐的数学人生.杭州:浙江大学出版社,2006.18.
29 Yau S T.The role of partial differential equations in differential geometry[M]∥Olli Lehto.Proceedings of the International Congress of Mathematics(Helsinki,1978)Vol.1.Helsinki:Acad.Scient.Fennica,1980.237 ~ 250.
30 Connor.J.and Robertson E F.Yau Biography.[DB/OL].[2010-11-15]http:∥www-history.mcs.st-and.ac.uk/Mathematicians/Yau.html
31 Yau S T.Calabi's conjecture and some new results in algebraic geometry[J].Proceedings of the National Academy of Science,1977,74(5) :1798 ~1799.
32 Yau S T.On the Ricci curvature of a compact Kähler manifold and the complex Monge-Ampère equation I[J].Communications on Pure and Applied Mathematics,1978,31(3):339 ~411.
33 Calabi E.Improper affine hyperspheres of convex type and a generalization of a theorem by K.Jörgens[J].Mich.Math.J,1958,5(2):105~126.
34 Kazdan J L.A remark on the preceding paper of yau[J].Communications on Pure and Applied Mathematics,1978,31(3):413~414.
35 Aubin T.Equations differentielles non lineaire et probleme de Yamabe concernant la courbure curvature[J].J.Math.Pures es Appl,1976,55(9):269~296.
36 En hommage a Thierry Aubin[J].SMF,Gazette,2009,(121):71 ~85.
37 Aubin T.Metriques riemanniennes et courbure[J].J.Diff.Geom,1970,4(4):383 ~ 424.
38 Aubin T.Equations du type Mongi-Ampere sur les varietes kahleriennes compactes[J].C.R.Acad.Sci.Hebd.Seances,A-B,1976,283(3):A119~A121.
39 Aubin T.Equations du type Monge-Ampere sur les varietes kahleriennes compactes[J].Bull.Sc.Math,1978,102(1):63 ~95.
40 Aubin T.Nonlinear Analysis on Manifolds,Monge-Ampère Equations[M].Berlin and New York :Springer-Verlag,1982.
41 Aubin T.Einstein-Kähler metrics[J].Rend.Sem.Mat.Univ.Pol.Torino.Fascicolo Speciale,1989:39 ~45.
42 Bourguignon J P.Premiere Classe de Chern et Courbure de:Ricci'Preuve de la Conjecture de Calabi(Seminaire,Palaiseau,1978) [M].Asterisque,no.58.Paris:Soc.Math.France,1978.
43 Bourguignon J P.Premieres formes de Chern des varietes kahleriennes compactes[J].Seminaire N.Bourbaki ,1979,1977/1978,exp.507~524:1~21.
44 Aubin T.Some Nonlinear Problems in Riemannian Geometry[M].Berlin Heidelberg:Springer,1998.
45 Besse A L.Einstein Manifolds[M].Berlin,Heidelberg,New York,London,Paris,Tokyo:Springer-Verlag,1987.3,96~97.
46 Moroianu A.Lectures on Kähler Geometry[M].Cambridge:Cambridge Univ.Press,2007.125 ~134.
47 Yau S T.Nonlinear analysis in geometry[J].Enseignement Math,1987,33(1 ~2) ,109 ~158.
48 Yau S.T.Open problems in geometry[M]∥Greene R,Yau S T.Proc.Sympos.Pure Math.Vol 54,Part 1.Providence:Amer.Math.Soc,1993.1~28(第65个问题).
49 Tian G.On Kähler-Einstein metrics on certain Kähler manifolds with C, > 0 [J].Invent.Math,1987,(89),225~240.
50 Tian G.On Calabi's conjecture for complex surfaces with positive first Chern class[J].Invent.Math,1990,101(1):101~172.
51 Tian G.Kähler-Einstein metrics with positive scalar curvature[J].Invent.Math,1997,130(1):1 ~137.
52 Donaldson S K.b-stability and blow-ups[DB/OL].[2011-09-02].http:∥arxiv.org/PS_cache/arxiv/pdf/1107/1107.1699v1.pdf
53 Donaldson S K.Stability,birational transformations and the Kähler-Einstein problem[DB/OL].[2011-09-02].http:∥arxiv.org/PS_cache/arxiv/pdf/1007/1007.4220v1.pdf.
54 Donaldson S K.Kähler metrics with cone singularities along a divisor[DB/OL].[2011-09-02].http:∥arxiv.org/PS_cache/arxiv/pdf/1102/1102.1196v2.pdf.
55 Chen X X,Donaldson S K.Volume estimates for Kähler-Einstein metrics:the three dimensional case[DB/OL].[2011-09-02].http:∥arxiv.org/PS_cache/arxiv/pdf/1104/1104.0270v2.pdf.
Abstract The proof of the Calabi Conjecture by Shing-Tung Yau in 1976 has generated a number of important results.These results are fundamental for the subsequent development of mathematics as well as that of physics.Based on the original literature,this paper outlines the origin of the Calabi conjecture and its final proof by Yau.The paper also discusses the close relation between the Calabi Conjecture and Kähler-Einstein metric through the work of Shing-Tung Yau and that of Thierry Aubin.
Key words Eugenio Calabi,Calabi Conjecture,Shing-Tung Yau,Thierry Aubin,Kähler-Einstein metric
The Calabi Conjecture and Its Proof
FENG Xiaohua,GAO Ce
(Research Center for Philosophy of Science and Technology,Shanxi University ,Taiyuan 030006,China)
N091∶O11
A
1000-0224(2012)02-0233-14
2011-05-13;
2012-02-10
冯晓华,女,1977年生,山西原平人,讲师,主要研究方向为近现代数学史,kinggirlss2001@sohu.com;高策,1958年生,山西太原人,教授,主要研究方向为科技史。
国家哲学社会科学基金(项目编号:08BZX020);教育部人文社科基金(项目编号:08JC0010)
