动平衡仪设计方法

2012-10-23张赞秋

制造技术与机床 2012年7期

张赞秋孙振高岩罗迪李俊

（大连光洋科技工程有限公司，辽宁大连 116600）

轴类旋转类件在高速旋转时，由于密度不均匀或者由于特异的外形将导致对支撑部位周期性的挤压或者拉伸，长时间将导致轴承的加速磨损和支撑物的金属疲劳，最终导致不可预计的安全隐患。因此对此类物件在使用前做基本运动平衡补偿是必须的，传统方式需要将被平衡物件拆卸后利用专用平衡机测量和补偿。本文描述的方法采用柔性比例估算方法，利用物件原始支撑不需要拆卸即可完成所有的补偿工作，可以提高工作效率和补偿成本。

1 平衡计算原理

当物体旋转时，如在径向存在不平衡，所有的不平衡量都可以递归到一个不平衡的质点和一个对应的有效半径，因此只要找到这个质点和有效半径，并且对此

质点做对应的反补偿，就可以平衡掉原有的不平衡量。

2 动平衡实现的方式

如图1所示，当物体以角速度ω旋转时，任意质点在XY坐标系的分速度分别为

其中θ为质点M的向径与X轴的夹角。

对式（1）、（2）求一阶导数得:

因此对于质点M，在XY方向的应力为

由式（5）、（6）可以看出当物体匀速旋转时，在X和Y方向的向心应力为一个正弦值。任何刚性支撑物都可以认为是一个弹性模型，即满足

式中:F为作用力;X代表形变有效形变量;k代表不同弹性模型的劲度系数。

因此满足在XY方向上有

由式（8）、（9）可以看出，在XY方向的位移同样是一种满足正弦加速的位移，也就是说通过测量支撑物的加速度就可以间接地测量出旋转部分的不平衡量。

3 实际存在的问题

采用转速传感器和加速度传感器对被测物的支撑体测量，寻找的被测物最大形变量的值，通过转速传感器对角度定位，就可以得到补偿点位置和补偿质量。

3.1 复合的信号与噪声问题

对于一个机械体，其在运行时往往是复合的特征反映，即在机械上所有的振动都将是一个相互耦合的关系，如图2所示。

图2表示的是某个带有小直径小惯量旋转部件的复合支撑物的振动波形图，由图可以看出所有的特征量被淹没在一片噪声中，因此对于有效直径小、不平衡量很小的旋转物体和刚度支撑较强的物体，希望直接利用加速度传感器和转速传感器，利用传统直接测试的方法基本是不可能的，因此必须采用某种方法对其有效信号进行提取。采用傅里叶变换可以精确对特征频率提纯，而且可以得到某个特征频率的幅值。

图3是利用傅立叶变换对某复合信号的分析波谱图，由图可以明显看到特征频率和幅值大小。因此利用傅里叶变换对振动进行频谱分析从而得到特征频率是有效而精确的。

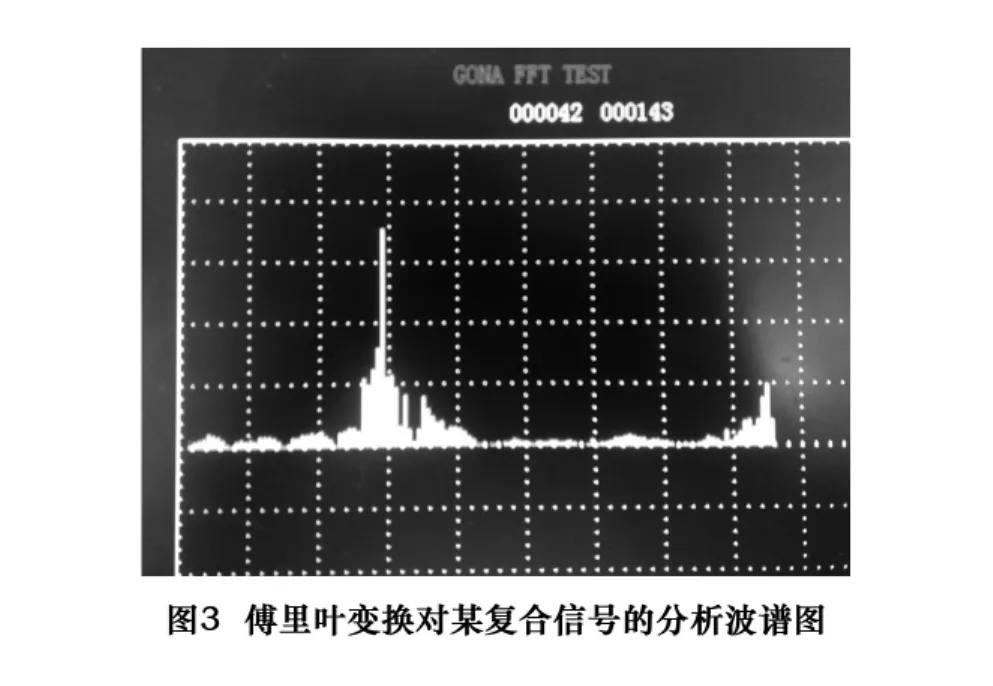
对于傅里叶变换来说，当实际频率超出采样频率的上下限时，在频谱图上将产生虚假频率，在计算时带来不必要的干扰误测。因此在采样之前必须对信号经过带通滤波处理，使被采样信号处在采样频率的极限之内，然后再进行频谱变换分析。

对于被测物体来说，情况是千差万别的，例如旋转部件的直径和最高转速。有些最高转速很低，例如大型转台60 r/min（1 Hz），电主轴30 000 r/min分（500 Hz），因此前级的带通滤波器的带通比为500∶1，这种宽范围的带通滤波器在现实中是不存在的，因此必须采用多通道带通滤波器选择滤波，并且为求更好的下行斜率每级采用2级带通滤波。

3.2 信号的幅值与精度问题

由于旋转部件的支撑物的刚度（劲度系数）差异和不平衡量各不一样，因此当振动量很小或支撑物刚度较强时，加速度传感器的输出幅值很小，造成采样精度过低。因此动平衡测试设备在前级输入端进行增益选择切换是必须的，以应付不同的输入幅值，提高补偿精度。

支撑物体的刚度不一致，必须求得支撑物体的刚度（劲度系数）才能最终得到需要的补偿量，也就是说必须对补偿量进行定标处理。因此在测量时首先对被测体进行测量，然后在被测体的随意位置安装一个已知质量、有效半径和角度的物体。然后再次测量，得到两次测量的差值，就可以推算出真实需要的补偿量的大小和位置。

4 实际问题分析与解决方案

4.1 噪声问题的处理

AD转换采样采用FPGA定时方式，为了提高数据的自我噪声抑制能力，采样采用硬件定时，采样后的数据由数学方式做滤波后进行FFT运算。

4.2 信号幅度的处理

由于信号幅度的不同，因此，信号在进入AD转换器进行转换前，采用了可变增益放大器进行数据放大倍数变更，此过程是一个自动完成的过程。

5 采用的方案

采用FFT处理器，为了提高运行速度，FFT运算采用硬件运算方式。

5.1 FFT 原理

快速傅里叶变换（FFT）是计算N点离散傅里叶变换（DFT）的高效算法，通常输入的序列为复数，利用对称性组合可以对实数实现更高效的DFT变换。

DFT是连续傅里叶变换的离散形式，模拟信号x（t）的连续时间傅立叶变换表示为

x（t）经抽样后变为x（nT），T为抽样周期。离散信号的傅里叶变换表示为

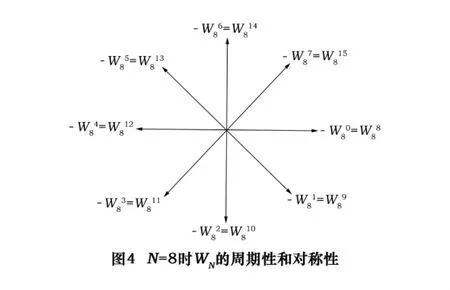
这样，利用这些特性可以使DFT运算中的某些项合并，可以将长序列的DFT分解为短序列的DFT。

FFT算法分为时间抽取FFT（DIT）和频率抽取FFT（DIF），DIT是将N点的输入序列x（n）按照偶数和奇数分解为偶序列和奇序列，因此，x（n）的N点FFT可表示为

根据

得:

用X1（k）和X2（k）分别表示式（14）右边第一项和第二项求和运算式，则有:

同理，进一步可得N/4点的FFT，重复抽取即可得2点FFT。在基－2FFT中N=2M，共有M级运算，每级有N/2个2点FFT蝶形运算，因此N点FFT共有（N/2）log2N个蝶形运算。基－2 DIT的FFT蝶形运算如图5所示。

DIF算法与DIT算法在本质上是一样的，在运算量与复杂性方面也完全相同，只不过它是把输出序列X（k）按其顺序的奇偶分解为越来越短的序列，这里只给出DIF的基本运算单元，如图6所示。

5.2 FFT处理器原理框图

FFT处理器的主要功能是对采集得到的数据进行512点FFT运算。其原理框图如图7所示。

地址控制模块负责产生读地址、写地址、使能信号以及相关模块的启动、控制信号，是本模块的核心;双口RAM负责对外部输入的原始数据进行缓存;蝶形运算单元完成2点DFT运算;旋转因子表实质上是一个ROM，用来存储每一级FFT运算所需要的旋转因子;暂存器RAM用来暂存经过蝶形运算后的中间数据;倒序模块实现频谱正常顺序输出;由于FFT的运算结果是复数，所以还需要对数据进行模值、相位角运算。