基于LE－SVM的切削颤振识别*

陈泽宇

（广州铁路职业技术学院，广东广州 510430）

切削颤振是金属切削过程中刀具与加工工件间自发的振动现象，它是影响工件表面质量的主要原因之一，是现代精密加工中必须解决的重要问题之一［1］。为了消除或抑制切削颤振的影响，多年来国际上众多学者对其机理、预报及控制等方面做了大量的研究，也取得了一些重要成果。文献［2］对比了多种颤振识别方法，并提出了结合PCA与SVM的识别方法。在实际声场中，颤振信号具有非线性、时变性和不确定性等特点，对这种非线性问题使用线性降维方法，难以得到满意的结果。本文对比了信号降维的方法，提出基于LE－SVM的切削颤振识别方法，并将其应用到实际切削加工识别中，获得较为满意的结果。

降维是指将样本从高维观测空间通过线性或者非线性映射投影到一个低维特征空间，从而便于从数据中提取用于识别的特征和压缩数据提高运算速度［3］。非线性降维（NLDR）方法很多，如等度规映射（ISOMA）、局部线性嵌入（LLE）、Laplace特征映射（LE）和局部保持投影（LPP）［4］。由于切削颤振信号集具有非线性特性，才有非线性降维方法能保持原始数据的拓扑结构不变，并能较好地解决数据处理中的“维数灾难”问题，本文利用这种优势建立了基于LE－SVM的识别方法［5］。

1 LE－SVM 方法

1.1 LE特征映射基本原理

一般的非线性维数约简方法简单描述如下:在Rl空间中给定一个有n个点的数据集合x1，x2，…，xn，则在Rm（m≤l）空间中找到对应的一套数据集合y1，y2，…，yn，使得yi代表xi［6］。

LE特征映射是一种使用特征向量求解的方法，它能保持数据点间的相对距离不变。由以下三步组成:

（1）构建邻域图

如果通过ε邻域法或K点最近邻域法确定xi和xj是邻近点，则把节点i和j连接起来。

（2）选择权重

有两种方法给边确定权重。其一，核函数方法:如果节点i和j被连接，则

否则，wij=0。

式中:e为指数函数的底值，为固定值2.718 28;t为高斯径向基核函数中心参数。

其二，简单方法:如果节点i和j被连接，则wij=1;否则，wij=0。

（3）特征映射

作为一般的特征矢量问题计算特征值和特征矢量的方程为

式中:D是对角权重矩阵，它的元素是权重矩阵W的行或列的总和，即:

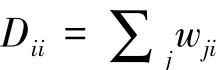
式中:拉普拉斯矩阵是:

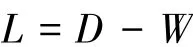
通过特征矢量问题式（2），可求得特征值λ和特征矢量f的值。并按特征值λ的大小排列特征矢量f，把对应特征值零的特征矢量删去，把余下的m个特征矢量嵌入m维欧拉空间中，如式（3）所示:

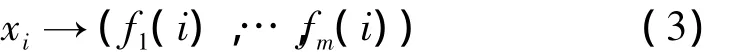
1.2 SVM支持向量机

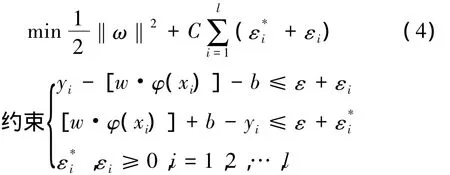
再构造Lagrange函数求解，根据Wolfe对偶规则转化为凸二次规划问题:

整理为标准形式，可得最优解:

根据最优解构造决策函数:

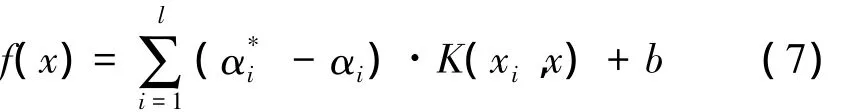
此即支持向量回归机的决策函数。根据决策函数能对样本集之外的新输入精确估计出相应的输出。文中选取应用最广泛的高斯径向基核函数。

1.3 基于LE－SVM的颤振训练和识别流程

基于LE－SVM的颤振识别方法主要包括两个阶段:训练阶段和识别阶段。训练阶段的工作流程:

（1）采集切削颤振的信号，构成信号样本集。（2）对采集信号进行小波滤波和归一化处理。（3）用LE算法对样本集进行分析，得到各状态下颤振信号的特征向量矩阵。

（4）把特征向量矩阵输入到支持向量机里进行训练，建立起切削颤振识别模型。

识别阶段的流程:

（1）采集切削颤振的信号，作为待识别的信号样本。

（2）对待识别的信号进行小波滤波和归一化处理。

（3）通过投影矩阵，把待识别的信号样本投影到训练阶段建立特征空间，得到待识别信号的特征向量。

（4）根据训练阶段建立的切削颤振识别模型对待识别信号的特征向量进行正常切削、颤振孕育、颤振爆发等分类。

2 颤振识别试验

2.1 试验的硬件和软件

为了检验LE－SVM算法识别的效果，需要进行颤振信号识别的试验。试验条件为:在TNL500数控机床上进行，工件材料为45钢，硬度为243 HB，无切削液润滑。电动机主轴转速300 r/min，进给速度30 mm/min，切削深度3 mm，刀具直径16 mm，其他切削参数为刀具前角 γo=12°，主偏角 κ=45°，后角 αn=8°，刃倾角λs=0。

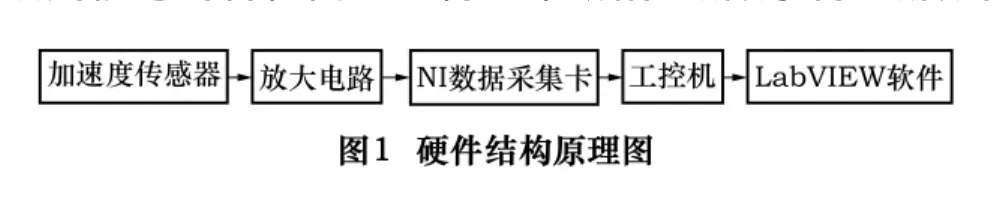
试验过程中，采用加速度传感器（HK9102）测量振动加速度信号，所测量的结果经过放大处理，输入到NI公司的数据采集卡USB－6221。硬件结构原理如图1所示。

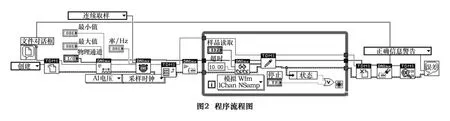
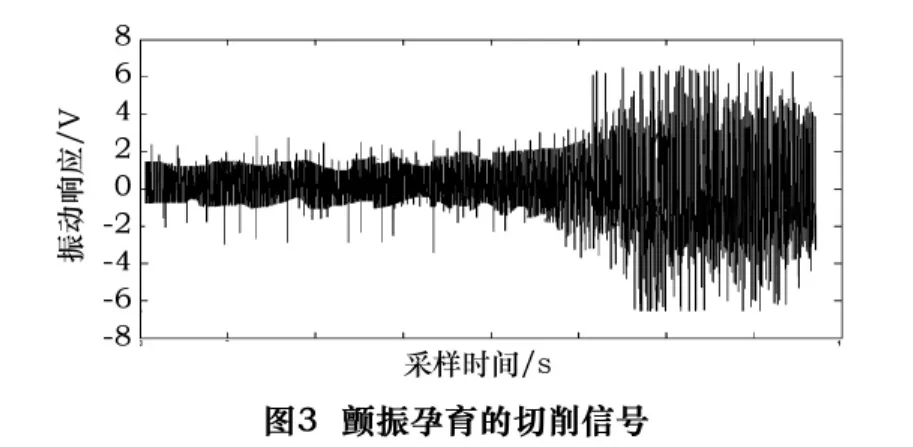
根据转速和采样定理要求，数据采集的采样频率为10 000 Hz，每个信号周期为1 024点，足以完整表达切削信号的特征。使用LabVIEW软件进行程序开发，其流程图如图2所示。图3为切削颤振孕育的切削信号。

2.2 颤振信号识别试验

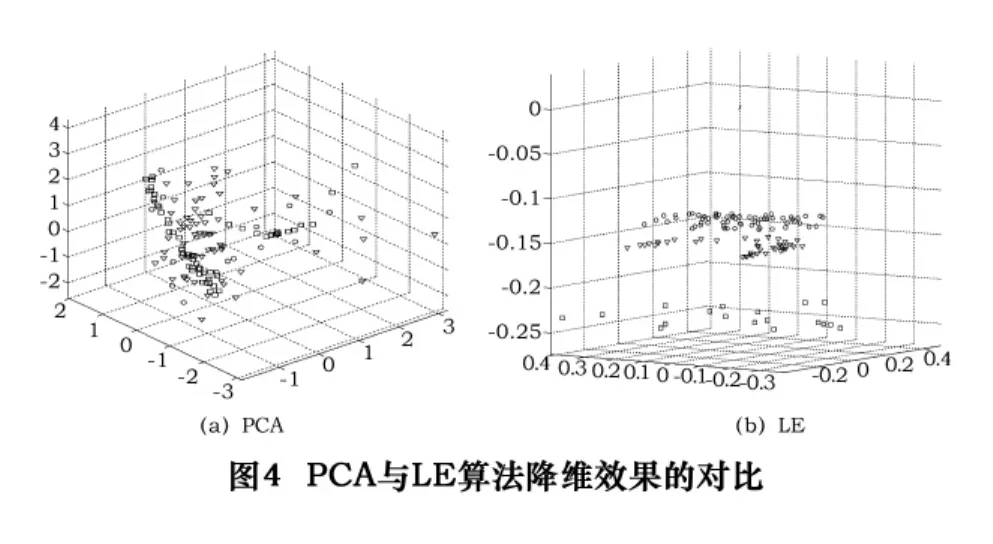
由于NI数据卡数据采集卡的采样频率为10 000 Hz，那么每个识别周期的切削颤振信号包含1 024个点，即为一个1 024维的向量。识别算法的运行速度与向量维数有直接的联系，向量维数越大运行速度越慢。1 024维的切削颤振信号作为识别模型的输入，将影响到识别系统运行时的反应时间。根据文献［5］可知，颤振识别信号中包含了大量的冗余并隐藏了重要关系的相关性，经过降维算法来消除冗余，减少被处理数据的数量。采集到的信号的长度为1 024维，经过降维算法分析信号样本，投影到可视的3维特征空间，图4为PCA与LE算法降维效果的对比。图4a为PCA降维后的效果，图中的三角形，圆形，方形分别代表正常切削、颤振孕育以及颤振爆发下的切削颤振信号。从图4a中可见，不同状态下的信号重叠，难以正确分类，将会提高SVM识别的准确度和运行速度。从图4b中可知，LE能成功地将多维非线性数据映射到三维空间中。分布在三维空间中的数据样本均不混叠，信号样本在三维维空间中仍能保持其相对独立性，证明LE算法降维效果是有效的。

为了检验LE－SVM算法分类模型的准确性，把90组数据集分为60组训练集和30组测试集。训练集用于基于LE－SVM分类模型的训练，测试集用于检验LE－SVM所建分类模型的识别效果。表1为切削颤振识别的结果。从结果上，识别的正确率高达为96.7%，满足正常使用;从运行速度上看，基于LE－SVM的平均运行时间只需0.093 s，能更高效快速识别出切削状态。

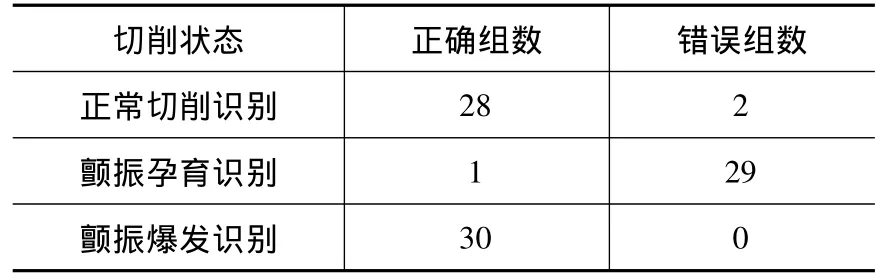
表1 切削状态LE－SVM识别结果

3 结语

在刀具颤振识别的建模过程中，利用LE算法进行降维，提高算法的泛化性和计算效率，建立了基于LE－SVM的刀具颤振识别模型，并将该模型应用于实际试验中。经实验结果分析表明，所建模型能正确反映刀具不同切削状态，识别正确率达96.7%，平均运行时间只需0.093 s，因此使用LE－SVM算法建立的切削颤振识别模型，可以快速有效识别出刀具切削状态。

［1］费仁元，王民.切削颤振在线监控的现状及进展［J］.中国机械工程，2001，12（9）:1075－1079.

［2］邵强.切削加工过程中颤振的监测与识别方法研究［D］.大连:大连理工大学，2010.

［3］李妍妍，李媛媛，叶世伟.基于流形正则化的支持向量回归及应用［J］.计算机应用，2007，27（8）:1955－1958.

［4］贾明兴，赵春晖，王福利，等.基于RBF神经网络的非线性主元分析方法［J］.仪器仪表学报，2008（3）:453－457.

［5］潘明清，周晓军，吴瑞明，等.基于主元分析的支持向量数据描述机械故障诊断［J］.传感技术学报，2006（1）:128－131.

［6］Belkin M，Niyogi P.Laplacian eigenmap and spectral techniques for embedding and clustering［C］.In:Proceeding of IEEE Advances in Neural Information Processing Systems.Canda:IEEE，2001:1373－1396.

［7］Schölkopf B，Smola A，Williamson R，et al.New support vector algorithms.NeuroColt2 － TR，1998［OL］.http://eiteseer.nj.nee.eom/276248.html