双周期复平面上的Cauchy-Pampeiu公式
2012-10-20宋伟林
宋伟林,刘 华
(天津职业技术师范大学汽车与交通学院,天津 300222)
复变函数方法是解决偏微分方程的一个有效工具。Bekua和华罗庚[1]在20世纪六七十年代对这一领域进行了全面深入的研究,以Cauchy-Pompeiu公式为基本工具,针对具体的区域给出解的明确积分表达式。相对于以广义函数为基础的定性讨论和以有限元法为代表的数值解法,复方法具有鲜明的特点。但后来由于对该方法所涉及的奇异积分缺乏合适的计算手段,该领域有较长时间的沉寂。近年来,由于计算机和计算技术(如奇异积分数值计算和边界元法)的发展,偏微分方程的复方法又引起了人们的注意。如,Abdymanapov等[2]在2005年研究了第一象限区域上的Schwarz问题;Wang[3]在2010年讨论了平面上扇形区域上的边值问题。
双周期平面上的偏微分方程理论有独特的地位。一方面,它的基本胞腔可以看做是复平面上的一个有界区域;另一方面,它又可以看做是一个非平凡的黎曼面。从前者看,困难在于双周期平面上不存在非平凡的全纯函数;从后者看,黎曼面的非线性会影响方程的可解性。本文主要研究带有双周期函数核的双周期复平面上的Cauchy-Pampeiu公式,希望借此解决双周期复偏微分方程。
1 预备知识
在这里需要给出一些基础知识。首先给出Green公式的复形式,即Gauss定理:设w∈C(1D;C) ∩C(;C)是复平面C 上正则区域D上的函数,则有
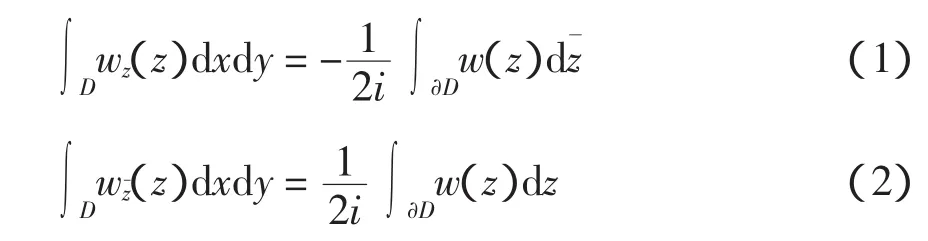
偏微分方程的复变方法理论中最重要的工具是Cauchy-Pompiu公式,它是通常的Cauchy公式对非解析函数的推广。
正则区域上的Cauchy-Pompeiu公式:设D⊂C是一个正则区域,w∈C(1D;) ∩C() ,设ζ= ξ+ ηi,则对z∈D有下面式子成立:
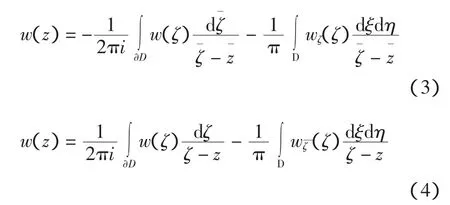
双周期函数是数学研究的重要对象,特别,解析双周期函数即为人们所熟知的椭圆函数,下面给出本文需要的相关性质。
双周期函数:设w1,w2是两个复数,满足Im()≠0。复函数f(z)称为以2w1,2w2为周期的双周期函数,若满足条件:
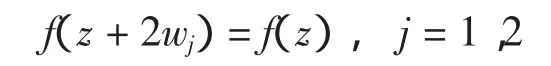
z′=z+2mw1+2nw2(n,m均为整数)称为与z周期合同的点。由非周期合同的点构成的最大的平行四边形称为周期平行四边形。特别地,以±w1、±w2为顶点的周期平行四边形称为基本周期四边形,记做P。函数
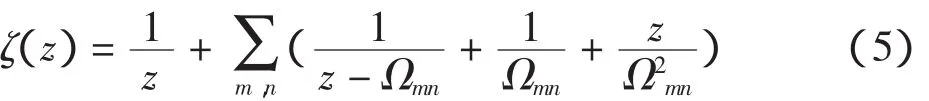
称为Weierstrass的ζ函数,其中Ωmn=2mw1+2nw2,且表示对一切m,n=0,±1,±2,L相加,但m,n不同时为0。
Weierstrass函数的一些性质:
ζ(z)是一个亚纯函数,以Ωmn(包括m=n=0)为单极点,且主部为1/z-Ωmn,但它不是双周期函数,而有

式中:ηj=ζ(wj)为常数,而且它在非零的周期合同的任意点是绝对收敛的。
因此,可以说对于任意非零的周期合同的点z,ζ(z)有界。
2 双周期平面上的Cauchy-Pompeiu公式
设P为上面提到的基本周期四边形,其边界不经过函数的极点。根据正则区域上的Cauchy-Pompeiu公式的共性知道,在讨论双周期平面上的Cauchy-Pom peiu公式时要有相当于Cauchy核的双周期核,它应与1/(t-z)相类似,在t=z处有一阶极点且留数为1。函数ζ(t-z)有此性质,但不是双周期函数。为了保证双周期性,这里用函数ζ(t-z)+ ζ(z)[4],但这样会引入单极点z=0。在后面的讨论中会看到这一奇异性对解决问题并无妨碍。
命题1:设函数g为一复函数,g∈C(1P;C) ∩C(;C) ,设t=x+iy,则对于z∈P有下面公式:
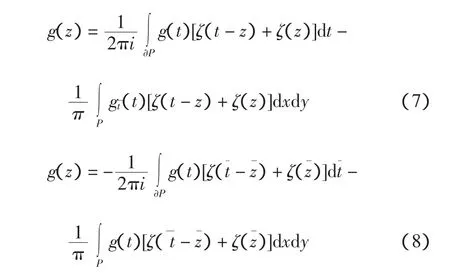
证明:这里仅就式(7)证明,式(8)的证明过程与(7)相似。

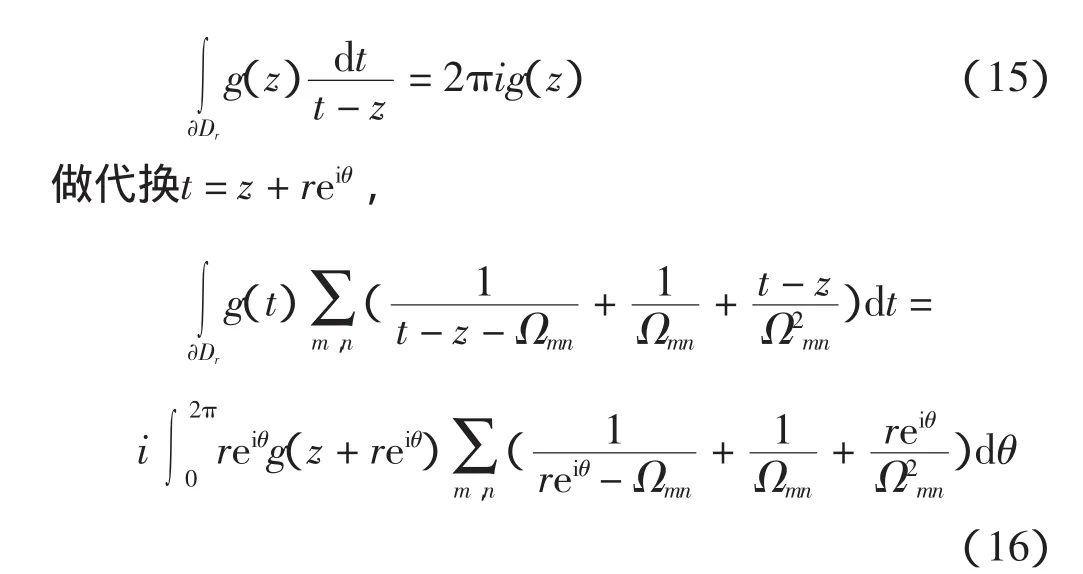
易知函数g(z+reiθ)和在θ∈[0,2π]上是有界的,所以当r→ 0时,上面积分→ 0。结合上面等式(9)~(14)得:

命题得证。
在应用中,常处理边界位于基本胞腔内部的区域上的问题,为此我们需要定义如下推论。
推论:设D为P中一区域,且其边界不经过ζ(t-z)的极点,f为一复函数,f∈C(1D;C) ∩C(),则对于z∈D有公式:
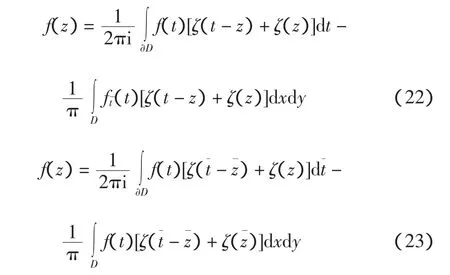
证明:假设极点t=z在域D外部,则正则区域上的Cauchy-Pampeiu公式成立,推论显然成立。
若t=z在域D内部,则上面命题的证明过程仍然成立,命题得证。
3 结束语
本文证明了双周期复平面上的Cauchy-Pampeiu公式的形式,并得到一个简单的推论,这给我们研究偏微分方程的双周期解提供了有力的工具,下一步的工作将是讨论双周期平面上的边值问题。
[1]HUA L K,LIN W,WU C Q.Second Order System of Partial Differential Equations in the Plane [M].London:Pitman,1985.
[2]ABDYMANAPOV S A,BEGEHR H,TUNGATAROV A B.Some Schwarz problems in a quarter plane [J].Eurasian Math,2005(3):22-35.
[3]WANG Y.Boundary value problems in a fan-shaped domain[J].Adv Pure Appl Math,2011(2):193-212.
[4]路见可.解析函数边值问题[M].2版.武汉:武汉大学出版社,2004.
[5]BEGEHR H,VAIEKHOVICH T.Harmonic boundary value problems in half disc and half ring[J].Functioneset Approximatio,2009,40(2):251-282.
