弹道导弹最大射程评定的T统计估计法

王瑞臣，李建林，杨海波

(海军潜艇学院，山东 青岛266042)

0 引言

导弹武器系统复杂，价值昂贵，特别是远程弹道导弹，由于试验次数很少，对其战术技术指标的试验分析与评估应用小子样的理论和方法具有明显的实际意义。最大标准飞行距离的估计方法一般都采用T统计法和Bayes方法。应用Bayes方法估计最大标准飞行距离比T统计方法精度更高［1］。但在用Bayes方法评定时，先验信息的来源及其可信度往往决定了评估的效果，如果先验信息数量过大，则有可能覆盖当前实际打靶样本;如果先验信息获取不正确，则评定结果的可信度难以保证。本文用T方法估计最大标准飞行距离，样本数量较多时，与Bayes方法评定结果相差较小。

1 最大标准飞行距离

由于试验的目的和任务不同，试验导弹的技术状态和使用导弹的技术状态存在着差异。为进行飞行试验评定，有必要规定一个标准条件，按照这个标准条件计算每发试验弹的最大飞行距离。

国家军用标准推荐一个供最大飞行距离评定使用的标准条件，具体如下:

1)武器系统为战斗状态;

2)液体推进剂按指定液位加注，常温推进剂加注温度为15℃，固体推进剂温度为20℃;

3)地球为匀质不旋转圆球，半径为6 371 110 m;

4)武器系统发射点和目标点均在地球表面，高程为0;

5)大气模型采用国家标准GB1920-80规定的标准大气模型，高空风速为0。

1.1 标准飞行距离

在标准条件下计算的导弹发射点至目标点的大地距离称为标准飞行距离。在实际飞行试验条件下获得的导弹飞行距离需转换为标准飞行距离后才能进行飞行距离评定。

1.2 试验最大飞行距离

试验弹在实际发射与飞行条件下，发动机继续工作至推进剂耗尽或发动机燃烧室压力下降至使反向喷管打开的最小值时所能达到的飞行距离称为试验最大飞行距离。

对固体燃料弹，推进剂达到动力系统能正常工作的最小剩余量时为推进剂耗尽。对液体燃料弹，由于其推进剂有2种原料，即氧化剂和燃烧剂，在实际飞行条件下，它们不可能同时耗尽，因此，其中任何一种原料达到动力系统能正常工作的最低液位就认为是推进剂耗尽。

试验最大飞行距离实际上就是单发弹在试验条件所能达到的最大飞行距离。

1.3 试验最大标准飞行距离

按照标准条件计算每发试验弹的最大飞行距离，即从试验最大飞行距离中扣除相对于标准条件的系统偏差对最大飞行距离的影响后得到的最大飞行距离称为试验最大标准飞行距离。

由于飞行中的试验弹受到许多内外干扰因素的影响，如自身的各种参数偏差等。因此，对一种型号或同型号的一个批次来说，试验最大标准飞行距离L是一个随机变量，服从一定的概率分布。固体导弹的试验最大标准飞行距离L近似服从正态分布，即

式中:μ为试验最大标准飞行距离的期望值;σ2为试验最大标准飞行距离的方差。

1.4 最大标准飞行距离

给定概率水平q，若下式成立

则称Lmax为概率水平q下的最大标准飞行距离。

根据国军标，q取99%或98%。若f(L)为L的概率密度函数，那么Lmax满足

从式(2)和式(3)可以看出，最大标准飞行距离是试验弹推进剂耗尽时所能达到的飞行距离的下界，即最大标准飞行距离是试验最大标准飞行距离的下界，最大标准飞行距离Lmax与概率水平q的取值有关，q越大，Lmax越小;反之亦然。

2 T统计估计法

2.1 T统计估计法

由试验最大标准飞行距离正态性假设式(1)与最大标准飞行距离的统计学定义式(2)可得

于是

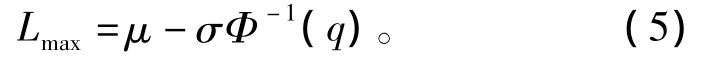
式中:Φ(x)为正态分布函数;Φ-1(x)为Φ(x)的反函数。

设有n个试验最大标准飞行距离L1，L2，…，Ln，样本均值与样本标准偏差分别为

则当σ已知时，Lmax的点估计为

当σ未知时，Lmax的点估计为

由

则

另

作统计量

T的概率密度为

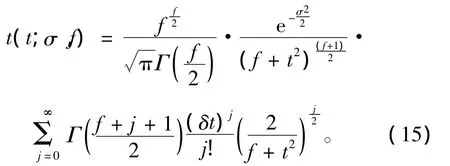
对于给定显著性水平α，最大标准飞行距离Lmax置信度为(1-α)的置信下限估计为

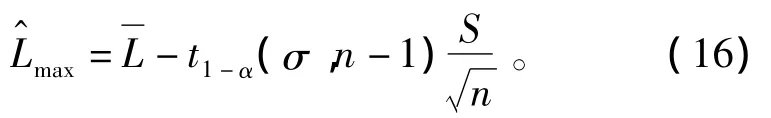
式中:t1-α(σ，n-1)为非中心 t分布 t(t;σ，f)的(1-α)的分位数

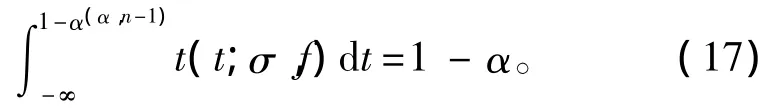
为提高计算精度，本文用数据拟合方法求解分布函数。

2.2 确定分布函数

在将各分布函数线性化的基础上应用线性回归分析将子样试验数据用各分布去拟合，在满足显著性水平的条件下选取相关系数r的绝对值最大的一个作为母体的分布函数。通过线性回归分析可以得到分布函数中参数的估计值。由回归分析知这样确定的参数估计值是最佳线性无偏估计［6］。

设随机子样T=(t1，t2，…，tn)来自未知的总体分布F;R(T，F)为某个预先选定的随机变量，它是T和F的函数。现要求根据观测子样T=(t1，t2，…，tn)估计R(T，F)的分布特征，如均值、方差或分布密度函数等。

为此，首先对测试数据按从小到大的次序排列，如t1≤t2≤…≤tn。将此数据列成如表1所示。

表1 试验数据列表Tab.1 Test data

表1中，F(ti)为累积分布函数的估计值，对F(ti)的估计值有许多种，

式中i表示第i个数据，式(19)中的中位秩数值有表可查，式(20)是经验分布函数。

F(ti)选用那一个估计式要看具体情况而定。

2.3 求得分布函数参数

1)将分布函数线性化

正态分布函数为

式中-∞ ＜t＜∞，-∞ ＜μ＜∞，σ＞0。

令

得

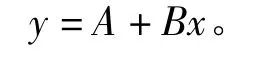
式中:A=-μ/σ，B=1/σ;Φ-1［t］为标准正态分布N(0，1)的分布函数的反函数。

2)计算A和B的估计值

3)确定随机变量T的分布函数

3 仿真计算

3.1 仿真条件

仿真以某弹道导弹为对象［3］，发射点经度110°，纬度26°，高程500 m;目标点经度112°，纬度22°，高程10 m。该导弹的实际打靶射程数据(单位:km):532.8，536.0，520.8，576.8，542.4，528.0，548.0。

文献 ［3］对上述打靶数据采用Bayes方法进行射程评定，其先验信息采用在标准弹道的基础上加入各项射击精度影响因素的干扰，并对推力偏差进行蒙特卡罗模拟后引入到干扰弹道中获得。仿真计算得到20个射程数据(单位:km):511.2，540.8，548.0， 520.8， 548.0， 519.2， 529.6， 559.2，528.8， 547.2， 559.2， 548.0， 527.2， 561.6，525.6， 549.6， 565.6， 536.0， 529.6， 555.2。Bayes评定为:最大射程分布为N(526.2，3.882)，Lmax=516 km。

本文对上述打靶数据用T统计估计法进行评定。

3.2 仿真计算

1)累积分布函数

将7个实际打靶射程数据和累积分布函数列表(见表2)。

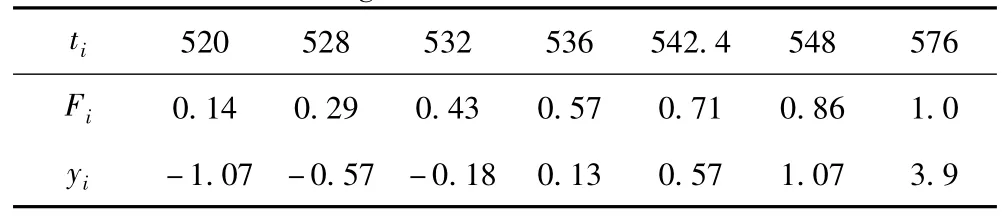
表2 射程数据、累积分布函数表Tab.2 Range data and distribution function

2)数据拟合

3)Lmax的下限估计

由式(9)得到Lmax的置信下限估计:置信度为0.98时，置信下限为506.9 km;置信度为0.99时，置信下限为502.5 km。

当用7个实际打靶数据，20个先验数据共27个对导弹射程评估时，得到下面的计算结果:

置信度为0.98时，置信下限为517.7 km;

置信度为0.99时，置信下限为514.7 km。

4 结语

为保证导弹武器系统战技性能指标评估的精确性和可信性，必须确保系统一定的试验量。随着试验次数的增加，战技指标评估的精度会提高，但是会出现增加费用，延长试验期限等问题。应用Bayes方法估计最大标准飞行距离比T统计方法精度更高，但若无验前信息可利用，或验前样本量也特小，此时应用Bayes方法，其估计精度也不理想。本文用T方法估计最大标准飞行距离，在试验样本数量较少时，其精度不高，在样本数量较多时，其评估精度较高。无论采用哪一种评定方法，样本数量多，其评定精度就高。因此，评定弹道导弹的最大射程应用何种估计方法，需要依据实际飞行试验情况决定。

［1］唐雪梅，张金槐，邵凤昌，李荣.武器装备小子样试验分析与评估［M］.北京:国防工业出版社，2001.55-81.TANG Xue-mei，ZHANG Jin-huai，SHAO Feng-chang，LI Rong.Test analysis and evaluation of weapon systems in small-sample circumstances［M］.Beijing:National Defense Industry Press，2001.55-81.

［2］祝强军，唐硕.弹道式导弹最大射程优化研究［J］.科学技术与工程.2007，7(5):2446-2449.ZHU Qiang-jun，TANG Shuo.Research on maximum range optimization of ballistic missile［J］.Science Technology and Engineering，2007，7(5):2446-2449.

［3］李刚，鲜勇，王明海.弹道导弹最大射程评定的Bayes方法［J］.弹道学报，2009，31(3):231-235.LI Gang，XIAN Yong，WANG Ming-hai.Bayesian method for evaluating ballistic missile's maximum range［J］.Journal of Ballistics，2009，31(3):231-235.

［4］张士峰，宫二玲.考虑可信度时导弹最大射程的Bayes评估［J］.国防科技大学学报，1999，21(4):17-21.ZHANG Shi-feng，GONG Er-ling.Bayesian evaluation of maximum distance considering credibility［J］.Journal of National University of Defense Technology，1999，21(4):17-21.

［5］许晓霞，唐胜景，钱杏芳，戴斌.抛射俯冲击顶弹道最小射程研究［J］.弹箭与制导学报，2005，25(1):172-175.XU Xiao-xia，TANG Sheng-jing，Qian Xingfang，Dai Bin.Study on the minimun range of the upper attack trajectory with projectile［J］.Journal of Projectiles，Rockets，Missiles and Guidance，2005，25(1):172-175.

［6］张训诰，肖德辉.可靠性及其应用［M］.北京:兵器工业出版社，1991.105-125.ZHANG Xun-gao，XIAO De-hui.Reliability and application［M］.Beijing:Weapon Industry Press，1991.105-125.