基于随机微分的质心干扰模型

胡生亮，杨 庆，贺静波，刘 忠

(1.海军工程大学电子工程学院，湖北武汉430033;2.南海舰队司令部，广东湛江524001)

0 引言

现代海战条件下，反舰导弹是水面舰艇面临的主要威胁。作为末端的质心干扰仍然是水面舰艇对抗反舰导弹的重要手段，在质心干扰情况下，反舰导弹末制导雷达对目标的跟踪问题也一直是相关研究领域的关注焦点，国内普遍采用Monte-Carlo仿真的方法进行研究，取得了一定的效果［1-4］。

目前，反舰导弹末制导雷达普遍采用了单脉冲跟踪体制，尽管质心干扰最终效能受多方面影响，但舰艇和干扰源的目标散射特性是影响质心干扰效能的最基本方面。因此，从目标散射特性和单脉冲末制导雷达对目标信号处理过程入手，是研究质心干扰效能一条可思考的途径。文献［5］从目标的散射特性角度研究了末制导雷达的捕捉概率问题，本文从信号层级入手，利用随机微分方程，研究质心干扰条件下反舰导弹末制导雷达的跟踪方位概率密度函数，并通过不同信噪比条件下跟踪方位概率密度函数曲线对比，验证本研究思路的有效性。

1 目标信号表示

根据基尔霍夫—惠更斯 (Kirchoff-Huygens)散射方程知反舰导弹末制导雷达散射场强为［6］

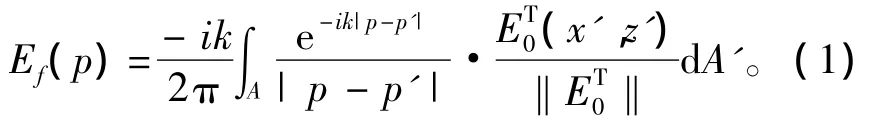
在远场近似条件下满足

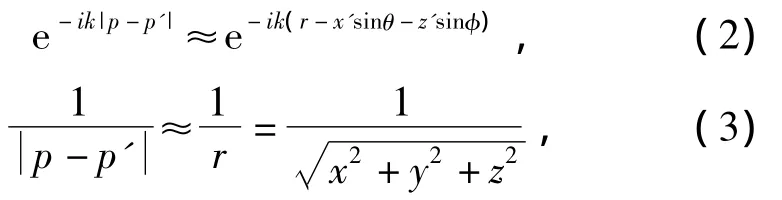
由此可得

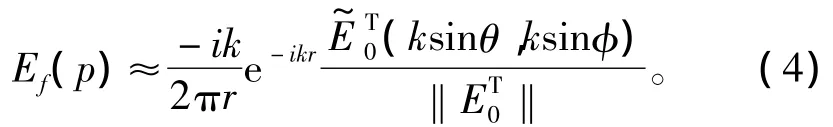
目标的后向散射场强为［7］

式中:θI和φI分别为目标方向的反舰导弹末制导雷达水平波束角度和垂直波束角度。这样在远场近似条件下反舰导弹末制导雷达天线表面的接收场强可表示为

设发射信号表示为R{F(t)eiωct}，相应的回波信号为 R{SR(t)eiωct}，其中

在远场近似条件下可得

其中，

式中，γ(r'，θ'，φ')为坐标变换系数。

设反舰导弹末制导雷达中频滤波器的响应函数为H(t)，则经过中频滤波后的输出信号S(t)为

式中，ξn为 ξ(r'，t)的离散化表示。

2 质心干扰模型

传统意义上研究质心干扰一般将目标的回波信号作为确定性变量分析，因而反舰导弹末制导雷达跟踪方位为目标的质心位置。但以上从电磁场分析的角度出发，可以看出目标的回波信号为一随机过程，所以导致反舰导弹末制导雷达跟踪方位亦应为一随机过程。基于此这里重点研究反舰导弹末制导雷达跟踪方位所满足的概率密度函数。

目标回波信号同时可以表示为

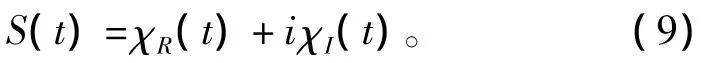
实部 χR(t)和虚部 χI(t)满足如下随机微分方程［9］:

式中W为维纳过程。由于目标的起伏特性，单脉冲体制的反舰导弹末制导雷达跟踪时其方位跟踪概率密度函数为［10］

其中，

式中:χ为信噪比;rJ为干扰源所在方位;rT为目标所在方位;I0和I1分别为一类零阶和一类一阶贝塞尔函数。根据上述方程就可以详细研究在质心干扰条件下反舰导弹末制导雷达的跟踪方位变化情况。

3 实验与结果分析

当信噪比χ=20 dB时，目标所在方位为rT=0°，干扰源所在方位为rJ=1°，此时反舰导弹末制导雷达的跟踪方位概率密度函数曲线如图1所示。

图1 方位跟踪概率密度函数曲线 (χ=20 dB)Fig.1 Azimuth tracking probability density function curve(χ=20 dB)

由图1可知，此时方位跟踪概率密度函数的极大值对应的跟踪角度近似为0°，即位于目标所在方位。实际计算中取值单位为弧度，而绘图时为了便于理解将其坐标值转换成了角度值，因此曲线实际积分面积为1(以下相同)。

其他参数不变，当信噪比 χ=0 dB时，反舰导弹末制导雷达的跟踪方位概率密度函数曲线如图2所示。

此时方位跟踪概率密度函数的极大值对应的跟踪角度近似为0.5°。

当信噪比时χ=-20 dB，反舰导弹末制导雷达的跟踪方位概率密度函数曲线如图3所示。

此时方位跟踪概率密度函数在干扰源附近出现2个极大值。

通过以上分析可以看出，不同信噪比条件下末制导雷达方位跟踪概率密度函数曲线结论与经典质心干扰效能分析研究的结果基本一致，且分析结果更加直观、更加符合实际跟踪情况，这面表明采用本文思路对质心干扰效果进行研究既具有一定可行性，又具有一定的先进性。

4 结语

质心干扰条件下，导弹末制导雷达对目标的跟踪本质上是对目标信号处理的过程。本文从目标散射特性角度出发，利用随机微分方程系统研究了单脉冲体制的反舰导弹末制导雷达跟踪问题，给出了质心干扰条件下反舰导弹末制导雷达的跟踪方位概率密度函数，并通过仿真实验验证了该模型的有效性。

［1］徐建萍，汤国建.反舰导弹目标捕捉概率的研究［J］.战术导弹技术，2008，(6):45-48.XU Jian-ping，TANG Guo-jian.Research on acquisition probability ofanti-ship missile［J］.TacticalMissile Technology，2008，(6):45-48.

［2］王斯福，张文义，刘永才，关世义.基于PSO的软杀伤对抗条件下反舰导弹捕捉概率优化研究［J］.兵工学报，2008，29(6):703-708.WANG Si-fu，ZHANG Wen-yi，LIU Yong-cai，GUAN Shiyi.Study of catch probability optimization for anti-ship missile on soft-killing condition based on PSO［J］.Acta Armamentarii，2008，29(6):703-707.

［3］吕彤光，姜文利，李盾，周一宇.两点源干扰情况下数据积累点数对雷达测角精度的影响［J］.国防科技大学学报，2001，23(5):48-53.LV Tong-guang，JIANG Wen-li，LI Dun，ZHOU Yi-yu.The effect of the number of radar accumulating data on the accuracy of angular measurement with interference of dual sources［J］.Journal of National University of Defense Technology，2001，23(6):48-53.

［4］沈培辉，王晓鸣，赵国志.无源电子对抗的质心干扰模型［J］. 弹道学报，1999，11(3):94-96.SHEN Pei-hui，WANG Xiao-ming，ZHAO Guo-zhi.Centroid mode on passive jamming［J］.Journal of Ballistics，1999，11(3):94-96.

［5］于录，李瑱.目标特性对反舰导弹捕捉概率的影响［J］.战术导弹技术，2010，(4):44-47.YU Lu，LI Zhen.Influence of target characteristics on the acquiring probability of anti-ship missile［J］.Tactical Missile Technology，2010，(3):44-47.

［6］HARGER R O.Synthetic aperature radar systems:theory and design［M］.Academic Press，1970.60-82.

［7］KRAUS J D，CARVER K R.Electromagnetics［M］.McGraw4Hill，1973.620-644.

［8］KERR D E.Propagation of short radio waves［M］.Boston Technical Publishers，Inc.，1964.455-450.

［9］OSTROVITYANOV R V，BASALOV F A.Statistical theory of extended radar targets［M］.Artech House，Dedham，MA，1985.10-15.

［10］KANTER I.The probability density function of the monopulse ratio for N looks at a combination of constant and Rayleigh targets［J］.IEEE Transction on Information Theory，1977，23(9):643-648.