船用激光陀螺惯导单轴旋转系统

可 伟，乔海岩，孟凡强

(中国船舶重工集团公司第三六八厂，河北邯郸056028)

0 引言

激光陀螺属于光学陀螺，其最大特点是设计简单，没有任何活动部件，启动时间短，动态范围广，尺度因数线性度好，不存在机电干扰等误差项，并且光学陀螺较其他机械陀螺的一大特点是适用于单轴旋转调制系统。

船用激光陀螺惯性导航系统［1］最大特点是在长航时应用，其长期导航精度很关键，而且作为舰船的核心主惯导设备，其承载着为舰船各武备系统提供基准的职责，故对其长航时位置精度以及姿态误差稳定性等指标要求很高。基于激光陀螺特点，针对船用惯导应用需求，要求所用激光陀螺指标极高，而精度极高的激光陀螺［2］其成本很难得到控制，并且到工程应用中，其量产存在很大问题。针对以上问题，我们提出了应用较高精度的光学激光陀螺，采用单轴旋转调制技术手段，在不增加系统成本的基础上，来提高系统导航精度。

单轴旋转调制技术是通过对IMU以一定方式旋转来达到常值漂移补偿的，在保证水平惯性器件输出精度没有改变的情况下，提高了系统长航时导航精度，尤其是系统位置精度。

1 单轴旋转调制机理

系统中，单轴旋转捷联惯导导航解算原理如图1所示。

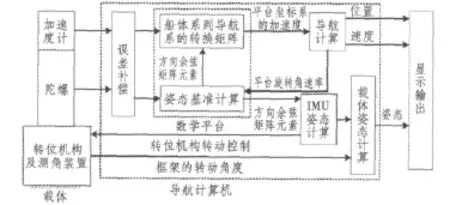
图1 单轴旋转激光捷联惯导系统工作原理Fig.1 Principles of single-axial rotation RLG SINS

系统方案设计中，IMU由3个二频机抖激光陀螺及3个石英挠性加表构成。旋转调制机构为速率旋转及位置锁定功能转台，该转台与IMU固联，并且使得IMU在安装过程中保证其垂向陀螺敏感轴与转台转轴平行，这样，固联的IMU相对于导航坐标系进行旋转。方案设计中，假设p系为转动坐标系，n系为导航坐标系［3］，i系为惯性坐标系，b系为船体坐标系。由单轴旋转惯导系统的工作原理，结合典型捷联式惯导系统误差方程，系统误差传播方程可描述为

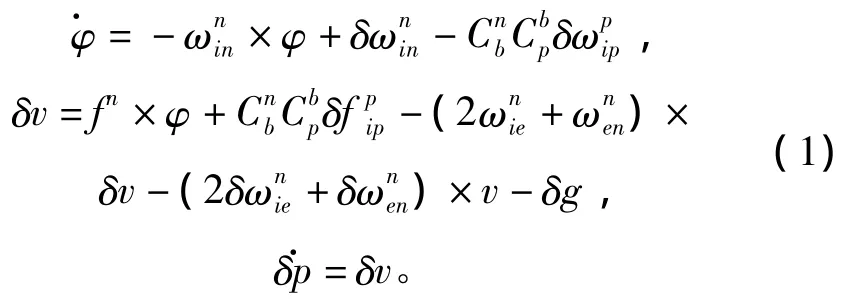
可以看出，方程(1)与传统典型捷联惯导系统误差传播方程的差异是陀螺及加表输出误差量在传播过程中发生了变换，并且构成的变换阵与时间有关。

方案中，假定在初始时转动坐标系p系与船体坐标系b系重合，且IMU绕天向轴旋转，则在任意t时刻，系统旋转角位置为θ(t)，那么根据上述假设，可得出从船体坐标系b系到旋转坐标系p系的变换矩阵为

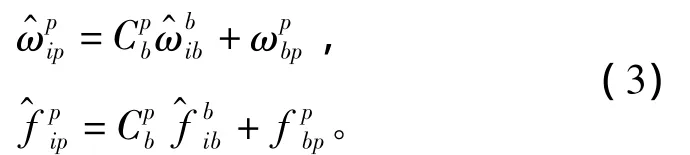
式(3)中，陀螺和加表的实测值在p系上的投影为:

将式(2)～式(4)代入式(5)中，得

由式(6)可得出结论，IMU中水平惯性器件输出误差在转位机构正反转停过程中被调制，且输出误差曲线按周期性规律变化，天向陀螺输出误差没有被调制。

捷联惯导系统误差传播方程中，等效北向和等效天向陀螺漂移会造成解算经度误差随时间而发散，因此将陀螺漂移对系统经度误差的影响单独列出进行考察。忽略交叉耦合项，静态下单通道误差模型为:

其中，εN和▽E为等效北向陀螺漂移和等效东向加速度计偏置。假设陀螺的常值漂移为εx，εy，εz加表零位偏置为▽x，▽y，▽z，则t时刻转换到导航坐标系上的陀螺和加表零偏可用下式表示:

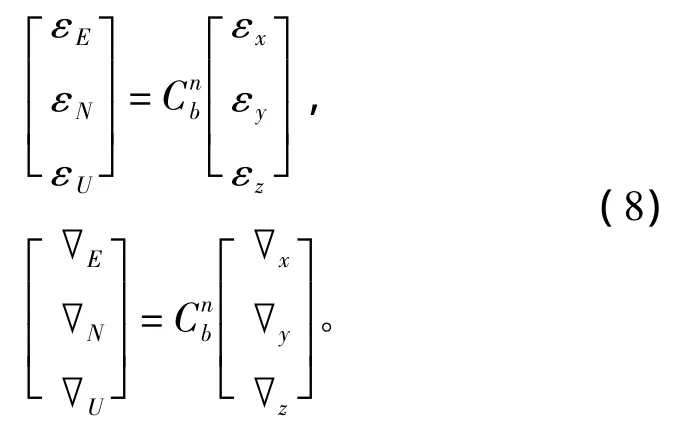
若仅考虑等效北向陀螺常值漂移，不考虑其余惯性元件输出误差、初值误差及重力加速度误差，略去航向角误差。单向通道的误差方程为:

绕航向轴旋转后，误差方程变为:

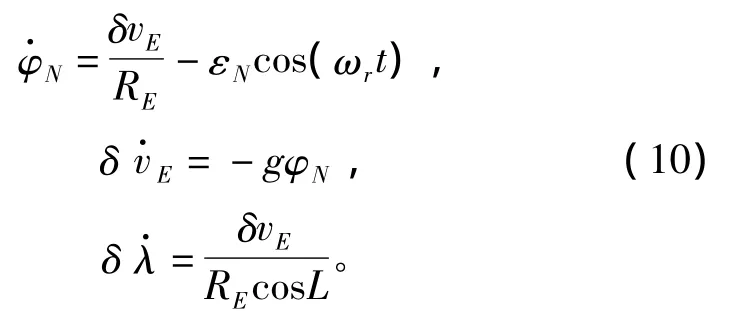
对式(9)和式(10)作Laplace变换，陀螺常漂视为阶跃信号

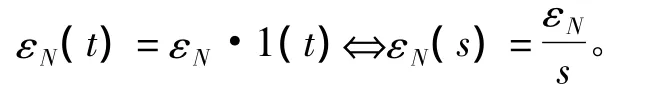
图2 北向陀螺漂移与经度误差关系框图Fig.2 The relation of north gyro’s bias and longitude error

由图2求得旋转系统误差解析式:

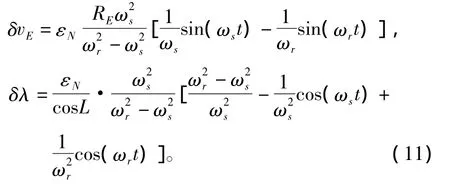
2 旋转方案设计

根据转动对称性要求，单轴旋转方案采用IMU单位置正反转停一周期方法实现惯性器件偏差的调制。

控制器控制执行机构使IMU在零位正反转停循环运动，并在固定位置上停留相同的时间，转动过程描述如下:

过程1:IMU在零位停留60 s;

过程2:IMU逆时针以6°/s的角速率旋转1周;

过程3:IMU在零位停留60 s;

过程4:IMU顺时针以6°/s的角速率旋转1周。

图3 IMU单位置正反转停示意图Fig.3 IMU signal-position clockwise and anti-clockwise rotation scheme

基于此种单位置正反转停［4］的旋转方式中，通过导航计算中积分作用，使得水平惯性器件常值漂移得以有效抵消，而天向陀螺常值漂移在旋转过程中并没有被调制掉。为获得高精度的激光惯导系统，有关重件陀螺的选型方面，采取了水平轴向惯性器件配置精度略差于天向惯性器件，这样，即可以节约系统整体成本，又可以充分发挥旋转调制技术作用，使得最终的系统满足现代军方要求，即打造低成本、中高精度及高可靠激光陀螺惯导系统。

3 计算机仿真验证

验证条件［5］:静基座下，陀螺常值漂移0.003°/h，陀螺随机误差0.0005°/h，陀螺标度因数稳定性0.466 ppm;加速度计常值偏置20 μg，加速度计标度因数稳定性20 ppm，陀螺组合件和加速度计组合件的安装误差均为［0，-2″，2″;2″，0，-2″;-2″，2″，0］。采用单位置转停方案，旋转速度6°/s，停止时间Th=60 s。采样周期1 s，仿真时间24 h。

企业要尽可能地提高会计信息的真实性和完整性，进而提高企业决策的准确性，就要加强企业财务管理，不断完善企业内控体系。一般来说，会计信息的真实性需要由内部控制制度提供保障，财务管理又对内部控制具有较大影响，所以，强化财务管理可以完善内部控制制度，使财务数据更加准确可靠，能在生产经营决策中发挥更好的作用，能更有效地规避企业经营风险。同时，企业内控体系并不是一成不变的，它会随着企业的发展不断变化，财务管理可以通过财务数据发现内控体系中的不足，从而依据这些信息对内控体系进行修改与完善，使内部控制制度能与企业的发展相适应。

仿真结果位置误差、东向速度误差、北向速度误差、水平误差和航向误差分别如图4～图9所示。在24 h工作时间内，位置误差小于1.1n mile，水平姿态误差小于0.01'，航向误差小于0.3'，速度误差小于0.06 m/s，可以满足船用惯导系统精度要求。

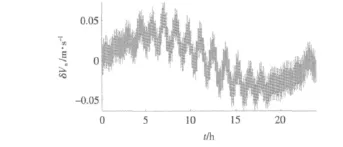
图9 24 h北速误差曲线Fig.9 The error curve of north velocity in 24 hours

4 系统设计

船用激光陀螺单轴旋转惯性导航系统主要由惯性装置、显控装置及电源装置等组成。其中惯性装置由IMU、单轴转位机构及缓冲基座组成;显控装置由显控机柜、显控计算机、加固型导航计算机、DC/DC模块、控制器、接口线路、减震器组件及对外转接组件等组成。电源装置由电源机柜、交直流变换线路、逆变器、蓄电池、充放电线路及隔离变压器等组成。其组成如图10所示。

图10 激光陀螺单轴旋转惯性导航系统组成Fig.10 Schematic representation of the single-axial rotating inertial navigation system

激光陀螺和加速度计构成的惯性测量组件与载体相对固联 (可绕方位轴旋转)，通过导航计算机采集惯性仪表输出的舰艇线加速度和角速度信息，经导航解算，输出舰艇位置、速度、航向、纵横摇和角速度信息。

惯性测量组件绕舰艇航向轴周期性旋转，使得水平轴惯性仪表常值误差对位置影响得以周期性抵消。

4.1 惯性测量单元

IMU是整个惯导装置的核心组件，其性能直接决定整个系统的成败。在结构布局上，3个机抖激光陀螺各自安装于磁屏蔽的陀螺盒内，然后3个陀螺通过螺钉正交安装固定于IMU上。3个石英加速度计是安装于1个加速度计基座上后，再将加速度计基座固定于IMU本体上，且尽量将加速度计放置于IMU的中心上。IMU集成了惯性元件信号处理线路，在IMU中完成信号预处理后再通过数字接口传输到显控装置电子线路组件中进行解算。

惯性测量组件与转位机构通过安装定位面保证重复安装精度，惯性测量组件可在海上更换而不须重新标校。

4.2 单轴转位机构

单轴转位机构上架设专用光学标校工具，测量设备基线面与舰艇基面的偏差，偏差量在舰船姿态计算中进行校正，无须进行机械调整。

旋转控制方案设计中，旋转调制采用交流伺服电机控制系统来实现。控制方案是一个典型的双闭环控制系统，控制系统采用全数字化。控制方案中，光电码盘等作为位置、速度反馈元件进行外环闭环。内环采用传统经典电流闭环控制回路，控制系统原理框图如图11所示。

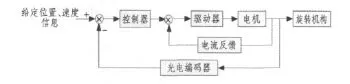
图11 旋转捷联惯导控制系统原理框图Fig.11 The elements representation of control system in rotation SINS

方案设计中采用交流电机、光电编码器(含细分盒)及交流电机驱动控制器为核心构建转位机构。其中，交流电机的转子与旋转机构框架进行同轴刚性固连，二者同步转停。这样一来，电机与转位机构的实际转角以及转速完全相同，便于后续的信息校对。转位机构内框设定有定位孔、基准靠面，以保证IMU的安装精度。

5 结语

系统设计中，根据船用惯导总体设计方案要求，较详细地介绍了船用激光陀螺单轴旋转惯导系统［6］总体组成及各分系统构成原理，针对总体性能指标要求，设计了各分系统控制策略，并结合激光陀螺及石英挠性加表特性，利用初始条件进行了系统仿真验证，仿真结果表明，采用单位置正反转停的旋转方案，其长航时导航输出精度明显优于同条件下传统非旋转情况下激光惯导输出指标，证实了该方案的可行性，为日后原理样机的研制提供了良好的研制基础。

［1］LEVINSON E，GIOVANNI C S.Laser gyro potential for long endurance marine navigation［C］.IEEE Position Location and Navigation Symposium.1980:115-129.

［2］HIBBARD R，WYLIE B，LEVISON E.Sperry marine MK-49，the world best ring laser gyro ships inertial navigation system［C］.JSDE Proceedings，Orlando，FL，November，1996.

［3］许国帧.惯性技术手册［M］.北京:宇航出版社，1995.

［4］袁保伦，饶谷音.光学陀螺旋转惯导系统原理探讨［J］.国防科技大学学报，2006，(6):76-80.YUAN Bao-lun，RAO Gu-yin.On the theory of optical gyro rotating inertial navigation system［J］.Journal of National University of Defense Technology，2006，(6):76-80.

［5］齐欢，王小平.系统建模与仿真［M］.北京:清华大学出版社，2004.

［6］张树侠，孙静.捷联式惯性导航系统［M］.北京:国防工业出版社，1992.