质子治疗装置大回转架支撑驱动系统的运动机理及分析
2012-10-16董思民蒋志强杜涵文
董思民 蒋志强 杜涵文
(中国科学院上海应用物理研究所 上海 201800)
质子治疗装置是粒子放射治疗的主流装备,由加速器及输运线和多个治疗室组成,治疗室分为固定治疗室和回转治疗室(Gantry治疗室)。固定治疗室中,治疗头水平放置,固定不动;回转治疗室中,治疗头及上游临近输运线安装在大回转架(Gantry)上,围绕等中心点作±185°旋转。支撑驱动系统是Gantry旋转的动力来源,使其进行高分辨率旋转并完成治疗头从任一角度对肿瘤照射,而不损害其他器官。Gantry支撑驱动系统设计的优劣直接影响最终治疗效果,因此须对Gantry支撑驱动系统进行设计分析。
1 结构和原理
1.1 结构组成
上海应用物理研究所研制的质子治疗装置Gantry总重约190吨,最大直径约15 m,长度约13 m。采用浮动叉式摩擦轮组支撑驱动方式(图1)。支撑驱动系统底座上对称焊接枢纽轴安装支耳,该枢纽轴用于安装等腰三角形结构的大三角立板,顶角处通过回转枢纽安装在底座上。在大三角立板的底角处各有一个枢纽轴,用于安装等腰三角形结构的小三角立板,顶角处通过枢纽与大三角立板相连,在其底角处安装支撑驱动滚轮,用于承载Gantry的前后环。因此,每个环共有8个支撑驱动滚轮支撑。由于每个滚轮的重量都超过30吨,根据其空间结构和承载特点,选用圆柱滚子轴承连接支撑驱动滚轮与小三角立板。支撑驱动系统的大枢纽轴与Gantry环中心组成等边三角形。同一环支撑驱动系统的底座间,用大梁连接在一起。如此的支撑组合,能达到自动取正平衡的效果。
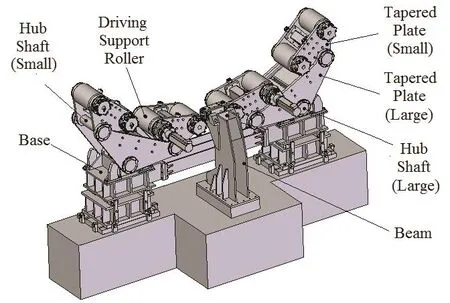
图1 Gantry 支撑驱动系统总体结构Fig.1 Overall structure of the gantry driving support system.
1.2 接触应力分析
Gantry环与支撑驱动滚轮接触区的压力分布符合赫兹接触理论,如图2所示,Gantry环与支撑驱动滚轮的接触区域并非直线,而是一个有效宽度为2a的矩形面。

图2 Gantry环与支撑驱动滚轮的赫兹接触Fig.2 The hertzian contact between the gantry wheel and driving support roller.
接触区的宽度和压力分布为[1]:

式中,P=PZ/B1为单位长度支撑驱动滚轮所受的正压力,B1是接触区域长度为滚轮长度,PZ是Gantry环施加在支撑驱动滚轮上的接触压力(单位:N/m);R为 Gantry环与支撑驱动滚轮相对曲率半径,与Gantry环半径R2和支撑驱动滚轮半径R1有关,可由1/R=1/R1+1/R2计算(单位:m);E*为Gantry环与支撑驱动滚轮的当量弹性模量,与支撑驱动滚轮弹性模量E1和泊松比v1及Gantry环弹性模量E2和泊松比v2有关,由 1/E*=(1–v12)/E1+(1–v22)/E2计算(单位:Pa);p(x)为沿Gantry环与支撑驱动滚轮接触面区域切线方向的分布压力(单位:Pa);x是接触面区域切线方向的坐标值,接触区域中间处x坐标为0。
由式(2),接触区的压力分布是一个抛物面。压力在接触区边缘降为零,最大压力出现在接触区的中轴线上:

由该设计,R2=2.7 m,B1=0.48 m,R1=0.18 m,它们的弹性模量均为2.1´1011Pa,泊松比0.3;则P=638125 N/m,a=2.5 mm。由式(3),最大接触应力为118 MPa。
1.3 弹性滑动下的传动比
Gantry支架重190吨,则Gantry环与支撑驱动滚轮间的压紧力达118 MPa,接触点处产生弹性变形,使实际传动比不能保持理论值,影响传动精度。图3是摩擦轮产生变形的示意图。

图3 弹性滑动原理图Fig.3 Schematics of the elastic sliding.
由于接触压紧力使材料产生弹性变形,接触部位为较小的接触面(接触区)。传递力矩时在接触面上产生摩擦力F,使表面产生剪切变形。F的方向在从动轮接触面上与从动轮的线速度方向相同,在主动轮接触面上与主动轮的线速度方向相反。因此,在主动轮轮1的接触区,表层金属将受到与线速度方向相反的剪切力和垂直于线速度方向的压紧力的联合作用;而在从动轮轮2的接触区,表层金属将受到与线速度方向相同的剪切力和垂直于线速度方向的压紧力的联合作用。显然,这种主、从动轮接触区所受方向相反的剪切力,会使主、从动轮接触区表面发生方向相反的剪切弹性变形,从而引起主动轮与从动轮表面在接触区内产生相对弹性滑动。
弹性滑动的结果使实际传动中,从动轮的圆周线速度v2小于主动轮的圆周线速度v1,即:

式中,∆v1、∆v2为主动轮和从动轮表层速度降低量,∆v即弹性滑动引起的从动轮速度损失。
弹性滑动的大小用弹性滑动系数ε表示:

Gantry环与支撑驱动滚轮接触采用钢-钢材料结构,ε=~0.2%[2],弹性滑动后,摩擦轮的实传动比按下式计算:

把几何参数代入式(6)得出:

由式(4)–(7)得出,i'12>i12,即实际传动比(15.03)大于理论传动比(15),精度偏差为0.2%。由上分析,摩擦轮传动中,弹性滑动造成速度损失,从而导致传动精度和传动效率降低。
Gantry环在 30°内从静止加速至最高转速 1 r/min,Gantry环的角加速度为β=0.01 rad/s2。传动比为理论值(15)时,支撑驱动滚轮的角加速度为0.15 rad/s2,传动比为实际值(15.03)时,支撑驱动滚轮的角加速度为 0.1503 rad/s2。两者相差 0.0003 rad/s2,支撑驱动滚轮驱动的转动惯量为 13570.7 kg×m2,因此,在转动惯量不变情况下,驱动扭矩变化为4.07 N×m,均在合理范围。
2 有限元模型
Coz等[3–6]采用有限元分析软件仿真接触力作用下各主要部件的应力和变形情况。但支撑结构接触力与接触变形的理论分析、用有限元接触法将支撑结构作为整体进行分析的研究不多,本文用Slid Edge进行支撑系统建模,由数据交换接口导入ANSYS Workbench[7]中。
有限元分析第一步将实体模型离散为若干单元组成的有限元网格模型,根据支撑结构的实际情况作如下简化:装配孔、螺纹孔和工艺孔对机构整体刚度的影响不大,且在划分网格时圆孔需作局部加密处理[8],这将增加单元数,加大计算量,因此,建模时忽略上述各类圆孔;所有小倒角、过渡圆角均用直角代替[9]。由于对称性,对结构的一半进行建模,减少了单元数计算量。建立的有限元模型如图4所示,共划分单元23588个,节点74464个。接触副的定义是求解接触问题的关键,给每个支撑驱动滚轮接触模型定义两个接触副,分别为滚轮两端凸轴与轴承内圈接触部分。
接触有限元模型的载荷包括支撑驱动滚轮的约束和压力。由于支撑驱动滚轮两端与轴承内圈是过盈配合,故令支撑驱动滚轮两端凸轴上的所有节点位移均为零。在质子治疗支撑系统的接触有限元分析中,支撑系统载荷分配不均对接触产生的影响,通过施加在支撑驱动滚轮上的压力大小和分布情况实现。每个支撑驱动滚轮在接触表面承受的径向压力和切向摩擦力以线载荷形式施加于滚轮表面上,其中支撑驱动滚轮承受的压力(306.3 kN)与摩擦力(10.7 kN)最大。

图4 支撑结构有限元模型Fig.4 Finite element model of the support structure.
3 有限元计算结果与分析
支撑驱动滚轮承受压力相对最大,主要分析支撑驱动滚轮的应力、变形。接触分析开始时Gantry环与滚轮的理论接触状态是一条接触线(刚好接触),随着计算时间增量逐渐发展为接触面。图5显示支撑驱动滚轮接触处位移分布和应力分布情况。在滚轮接触区与左侧面变形较大,接触区中部变形出现峰值。
由图5(b),接触区域的形状相似于矩形面,与赫兹接触理论所述“有效宽度为2a的矩形面”吻合。应力在接触处中部达最大值,远离接触处的应力接近于零。算得接触处的最大接触应力为122.6 MPa,与赫兹接触理论接触应力118 MPa相差约4%。
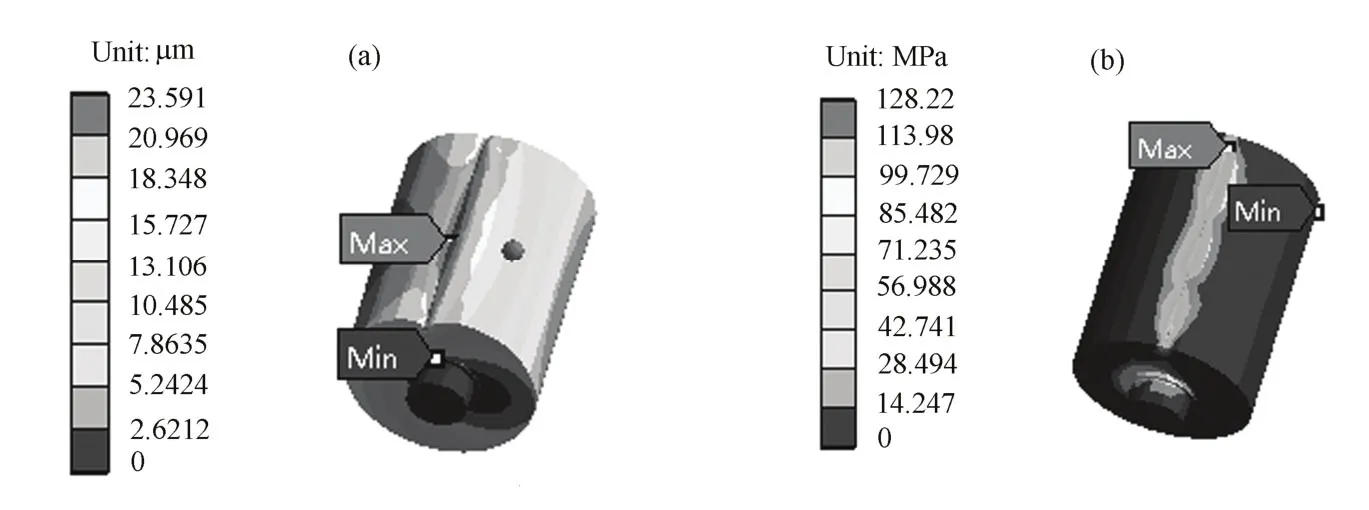
图5 支撑驱动滚轮变形云图(a)和等效应力云图(b)Fig.5 Deformation map of driving support roller (a) and stress map(b).
滚轮变形直接影响Gantry环的变形,滚轮工作状态直接影响设备的工作效率,了解滚轮接触区域的变形和应力情况,能间接反映出Gantry回转中心线的跳动情况。支撑驱动滚轮接触区域变形分布曲线见图6,最大变形出现在接触区域中间部位,因此,支撑驱动滚轮最危险部位在接触区域的中部。

图6 支撑滚轮变形分布曲线Fig.6 Deformation distribution curve of driving support roller.
小三角立板的变形如图7所示,边缘区域变形较大,中间区域变形较小。最大变形位置处于小三角立板下端,即小三角立板与大枢纽轴连接处,大小约0.13 mm。因此,在下一步优化设计中,考虑加厚小三角立板的厚度。
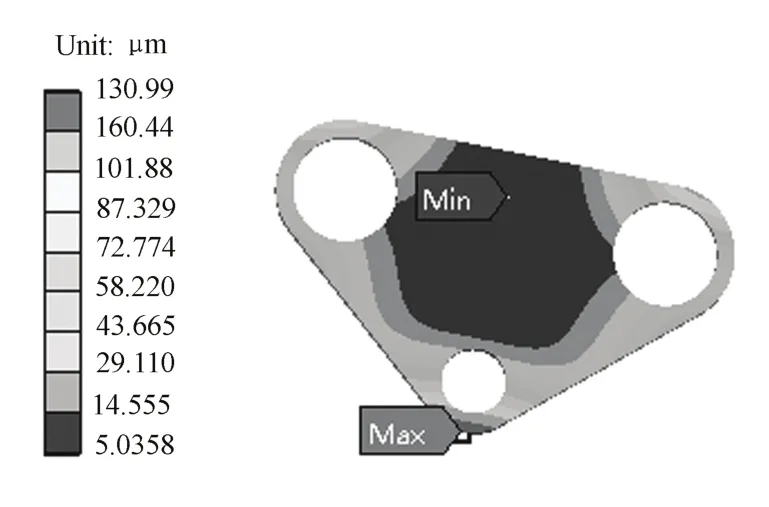
图7 小三角立板变形云图Fig.7 Deformation map of small tapered plate.
4 结语
(1) 由于摩擦轮间存在弹性滑动,实际传动比略大于理论传动比,支撑驱动滚轮角加速度值相应增大 0.0003 rad/s2,在转动惯量相同情况下,驱动扭矩也增大4.07 N×m。
(2) 有限元分析表明,支撑驱动滚轮受力变形最大,最大应力为122 MPa,和赫兹理论计算值相近,说明了分析的可靠性。
(3) 支撑驱动滚轮最危险区域位于接触表面中部,易发生接触疲劳。
(4) 在滚轮回转过程中,每一点的变形均呈现凹凸交变的复杂状态,从而迫使Gantry环变形凹凸交变。设计时应保证Gantry本体具有足够的刚度和疲劳强度,以限制本体变形及疲劳破坏,防止发生事故。
1 Mgladwell G. 经典弹性理论中的接触问题[M]. 北京:北京理工大学出版社, 1992 Mgladwell G .The contact problem under classical elastic theory[M]. Beijing: Beijing Polytech Press, 1992
2 徐峰. 精密机械设计[M]. 北京: 清华大学出版社, 2005 XU Feng. Precision mechanical design[M]. Beijing:Tsinghua Univ Press, 2005
3 Coz Díaz J J, Rodrí Mazón F, García Nieto P J. Design and finite element analysis of a wet cycle cement rotary kiln[C]. FEA Des, 2002, 39(1): 17–24
4 Bouzaikis K D, Siganos A. FEM supported determination of cement rotary kiln stresses considering the contribution of the internal refractory to the kiln rigidity[C]. Zement-Kalk-Gips ZKG International, 2004, 57(2): 70–78
5 周 贤, 刘义伦, 赵先琼. 回转窑轮带受力模型及接触应力仿真分析[J].中南工业大学学报, 2002, 33(5):526–529 ZHOU Xian, LIU Yilun, ZHAO Xianqiong. Mechanical model and contact stress emulational analysis of rotary kiln’s type[J]. J Cent South Univ Technol, 2002, 33(5):526–529
6 赵先琼, 刘义伦, 周 贤. 回转窑托轮力学行为的有限元分析[J]. 湖南大学学报(自然科学版), 2002, 29(6):526–529 ZHAO Xianqiong, LIU Yilun, ZHOU Xian. Finite element ananlysis of mechanical conditions for supporter of rotary kiln[J]. J Hunan Univ(Natural Science), 2002,29(6): 526–529
7 李 兵, 何正嘉, 陈雪峰. ANSYS Workbench设计、仿真与优化[M]. 北京: 清华大学出版社, 2008 LI Bing, HE Zhengjia, CHEN Xuefeng. ANSYS Workbench design, simulation and optimization[M]. Beijing:Tsinghua Univ Press, 2008
8 曾 攀. 有限元分析及应用[M]. 北京: 清华大学出版社,2004 ZENG Pan. Finite element analysis and applications[M].Beijing: Tsinghua Univ Press, 2004
9 钱德拉佩特拉T R, 贝莱冈度A D. 工程中的有限元方法[M]. 第3版. 北京: 机械工业出版社, 2006 Chandrupatle T R, Belegundu A D. The finite element method in engineering[M]. Third Ed. Beijing: China Mach Press, 2006
