上海质子治疗装置慢引出RFKO研究

史 丹 欧阳联华 谷 鸣

(中国科学院上海应用物理研究所 上海 201800)

质子束治疗癌症优于常规射线治疗(电子、X射线、γ射线)。治疗控制要求加速器提供均匀、稳定且快速开关的束流，其占空比须可调。因此，采用同步环慢引出的方式。医用质子加速器慢引出设计中，将质子从环内引出有两类方法。

第一类方法是将相空间稳定区三角形面积压缩，使稳定区外围粒子进入共振。相空间三角形面积与规一化六极磁铁强度的平方成反比，与粒子的tune值与三阶共振频率的距离平方成正比。减小相空间三角形面积可增大六极磁铁强度；或调节四极磁铁强度使粒子的tune值逼近三阶共振线，此方法需改变环束流的光学参数[1]。

第二类方法是先调节束流参数(发射度，tune值等)至临界值，维持不变，通过激励使粒子进入共振。一是纵向激励，如使用betatron core和纵向随机电场(stochastic noise)加速(或减速)，提高粒子进入共振的速度，使不同动量的粒子同时进入共振。我们采用横向 RF-knockout(RFKO)电场激励，使粒子发射度增长，被“打”出稳定区(knockout)，进入共振。首先是稳定区外围振幅大的粒子溢出稳定区，然后是稳定区中心区域的振幅较小的粒子也被激励，溢出稳定区，直至所有粒子均被引出。

RFKO的优点是：(1) 引出时环的Lattice参数保持不变；(2) 粒子引出时进入septum的横向位置(spiral step)保持不变；(3) 若与RF cavity纵向电场配合，粒子的关断时间可达100 µs，宜于开展高精度的呼吸门控和点扫描治疗。RFKO方法要求环色品很小(最好为 0)，则不同能散的粒子具有相同的tune值，不会通过同步振荡进入共振。但是零色品的环易引起束流头尾不稳定性[2]。

1 RFKO理论基础

1.1 三阶共振Hamiltonian函数

不考虑偏能粒子和闭轨畸变，粒子运动归一化相空间的Hamiltonian方程[3]为

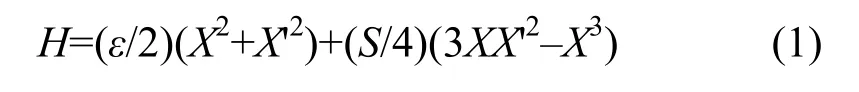
其中，ε= 6πδQ，δQ为粒子tune值离三阶共振的距离，S为六极铁强度，X、X'为坐标。由式(1)可得三阶共振的稳定区和非稳定区及其边界(separatrices)和稳定点以及稳定区面积，分析粒子在稳定区内、边界上和稳定点附近的运动行为。

定义粒子的归一化振幅和发射度分别为A=(X02+X0'2)1/2，E=πA2。引出时，调整四极磁铁的强度以改变 tune值的距离δQ，同时调整六极磁铁的强度S，相空间椭圆变成三角形。若粒子振幅小于稳定三角形面积Estable，该粒子是稳定的。

对于某一个特定振幅，δQ小于以下值时粒子将失去稳定：

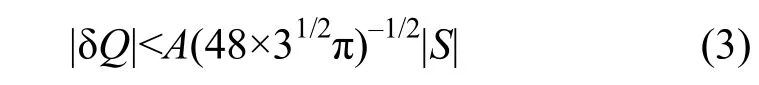
同样，对某一个特定的δQ，粒子振幅大于以下值时，将失去稳定：

1.2 RFKO理论基础

当环上存在RF kicker(这里简化为横向RF正弦振荡)时，Hill方程[4]变为：

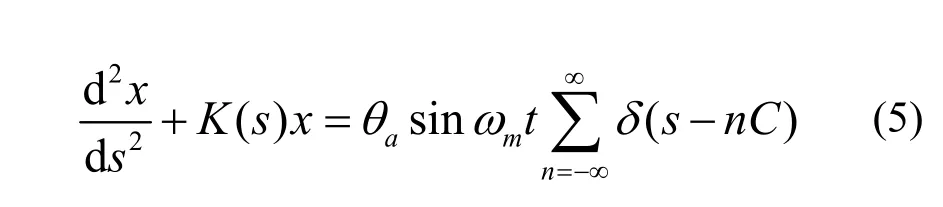
式中，K(s)为环聚焦强度，θa为横向RF kicker强度，ωm为其频率，t=s/(βc)，δ函数表示粒子每循环一圈被激励一次。

对式(5)进行 Floquet变换，求解变换后方程的特解和通解, 并给定初始条件x=x'=0；当RF kicker频率与粒子回旋频率之比vm等于或接近 tune值v时，式(5)的解为：

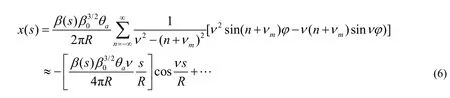
其中，R为环周长，β0为RF kicker所在处的β函数。

上海质子治疗加速器环周长28.4 m，v=5/3，图1为受RF knockout激励粒子横向位置随时间变化结果，可见振幅为0的粒子，经RF kicker激励，振幅呈振荡性线性增长。

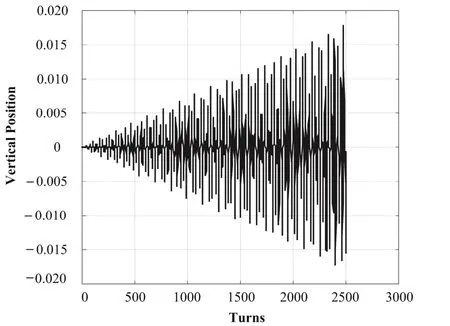
图1 受RF knockout激励，粒子横向位置随时间呈振荡性线性增长Fig.1 The horizontal position of particles vs the time.The position oscillation grows linearly with the time,due to RF knockout motivating.

2 幅度调制(AM)

RFKO可增大引出粒子的振幅，扩大其发射度，使粒子溢出稳定区而被引出，但引出束流的幅度与RFKO的踢角并不呈线性关系。根据HIMAC资料[5]，对于随机RFKO电场信号，1σ偏差可达±70%，调制后1σ偏差<±20%。因此，AM调制以达到预想的引出束流幅度结构及引出效率，是非常关键的。可使用简化的一维模型获得AM函数[6]，得到平滑束流。径向分布函数在规范化的相空间可写成瑞利分布，即

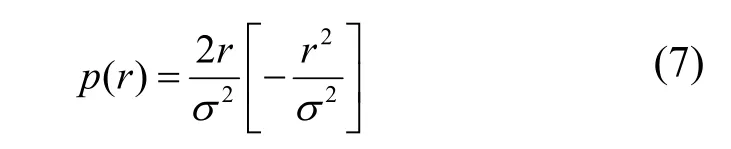
其中，σ2=2εrms，σ为瑞利分布的标准差，εrms为均方根发射度。

假设径向幅度大于0r的会被引出，引出粒子数为extN，引出束流的时间结构为

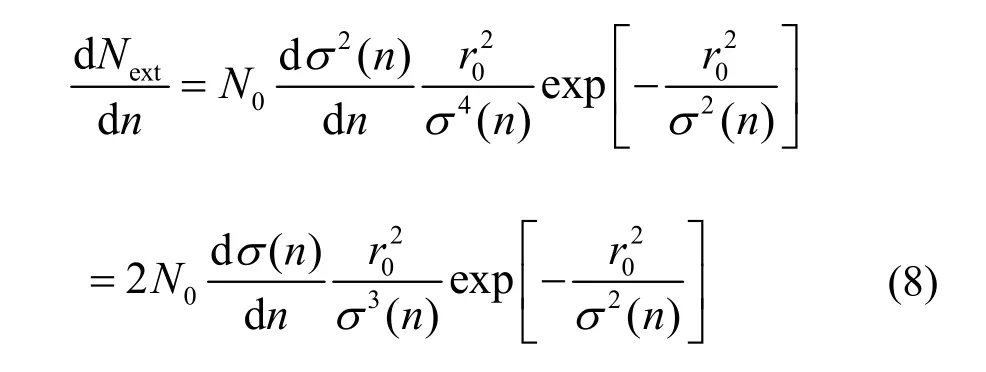
N0为引出前环内的粒子数。假定σ2与粒子转的圈数成正比，kick角幅度θ依赖于时间，使用常数k指代与RFKO带宽相关的系数，则σ值的增长为：

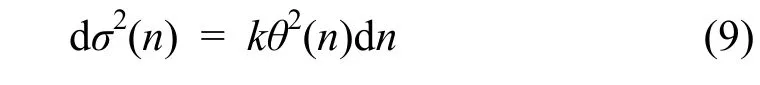
为获得平滑的溢出且引出所有粒子，dNext/dn引出时保持不变，则平滑引出的AM函数为

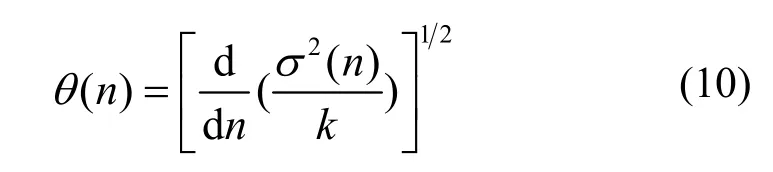
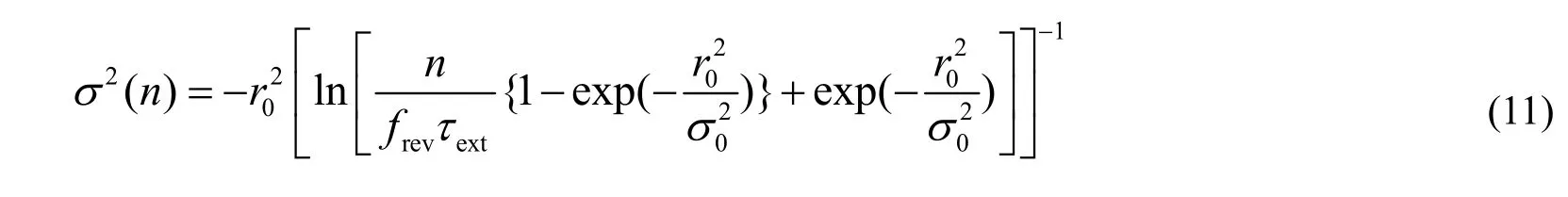
式中，σ0为σ(n)的初始值，τext为引出持续时间。估算k=312，r0=9.09×10−3，σ0=3.16×10−3，kick 角分别为0.5、1.0、2.0 µrad，引出时间结构的解析曲线如图2。若每圈引出1000个粒子, 则θ和n的关系如图3。

图2 恒定kick角下的引出时间结构, Kick角分别为 0.5、1.0、2.0 µradFig.2 The extracted spill structure at kick angles of 0.5, 1.0 and 2.0 µrad.

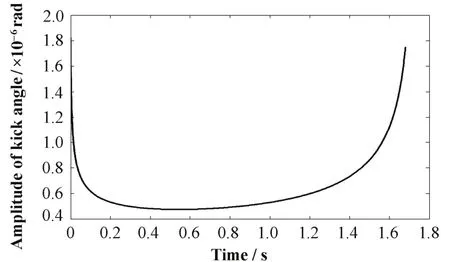
图3 θ和n的关系曲线(每圈引出1000个粒子)Fig.3 The θ-n curve, with an extracted beam of 1000 protons.

3 数值模拟

3.1 引出粒子分布情况模拟

运用软件 WinAGILE[7]研究粒子引出情况，设置动量偏差(dp/p)后，高斯粒子束散布在三角区内，引出初期，一部分不稳定粒子进入非稳定区，进而被引出，且引出粒子数服从指数分布；由于动量偏差，粒子束开始向静电切割板即不稳定区域移动。加速若干圈后，粒子被引出，引出数目和圈数服从高斯分布(图4a)。同样设置动量偏差，1000个均匀分布粒子引出亦服从均匀分布(图4b)。与高斯分布不同的是，分界线内的粒子在全部引出前，不稳定粒子未被引出。

3.2 Tune值与引出粒子关系

调整四极磁铁强度即改变ΔQ，保持Δp/p=0，且S= –4.2259不变，得到临界值 ΔQ=|Qp–Qr|=0.004202，Qr即tune值5/3，此时四极磁铁强度QF为–2.109732。表1显示，|ΔQ|<0.004202，有粒子被引出；相反，则无粒子被引出。ΔQ接近0时，粒子几乎完全引出，|ΔQ|逐渐增大，粒子引出数相应减少。

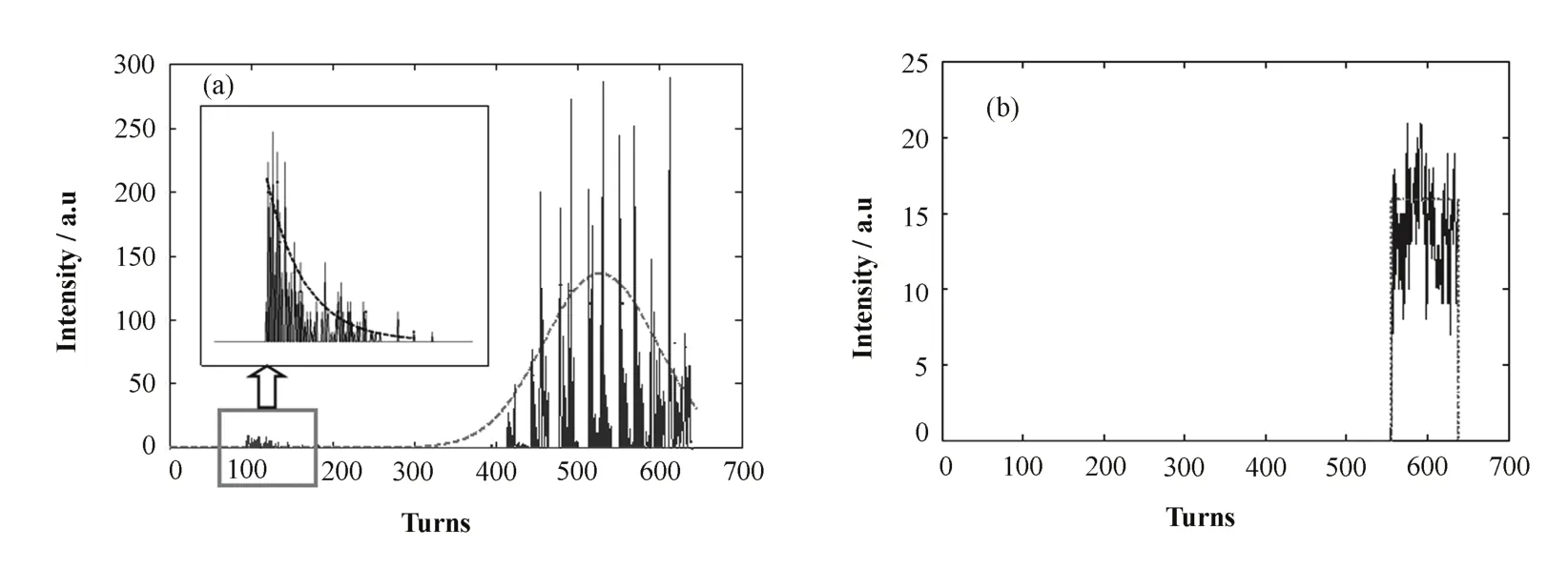
图4 5000个高斯粒子(a)和1000个均匀分布粒子(b)的引出图Fig.4 Extraction of 5000 Gaussian particles(a) and 1000 uniform distribution particles(b).

3.3 共振驱动六极磁铁强度与引出关系

保持能散不变(Δp/p=0)，ΔQ =–0.003609 不变，模拟发现六极磁铁强度S的临界值为–3.5(表2)。对S值和剩余粒子数拟合，得到拟合函数式Nremain=373.6e0.01638S+1123e0.1549S(图5)。|S| = –3.5, 粒子几乎无引出，在六极磁铁强度不断减小，即|S|逐渐增加时，粒子慢慢被引出，模拟仿真验证了相关理论。

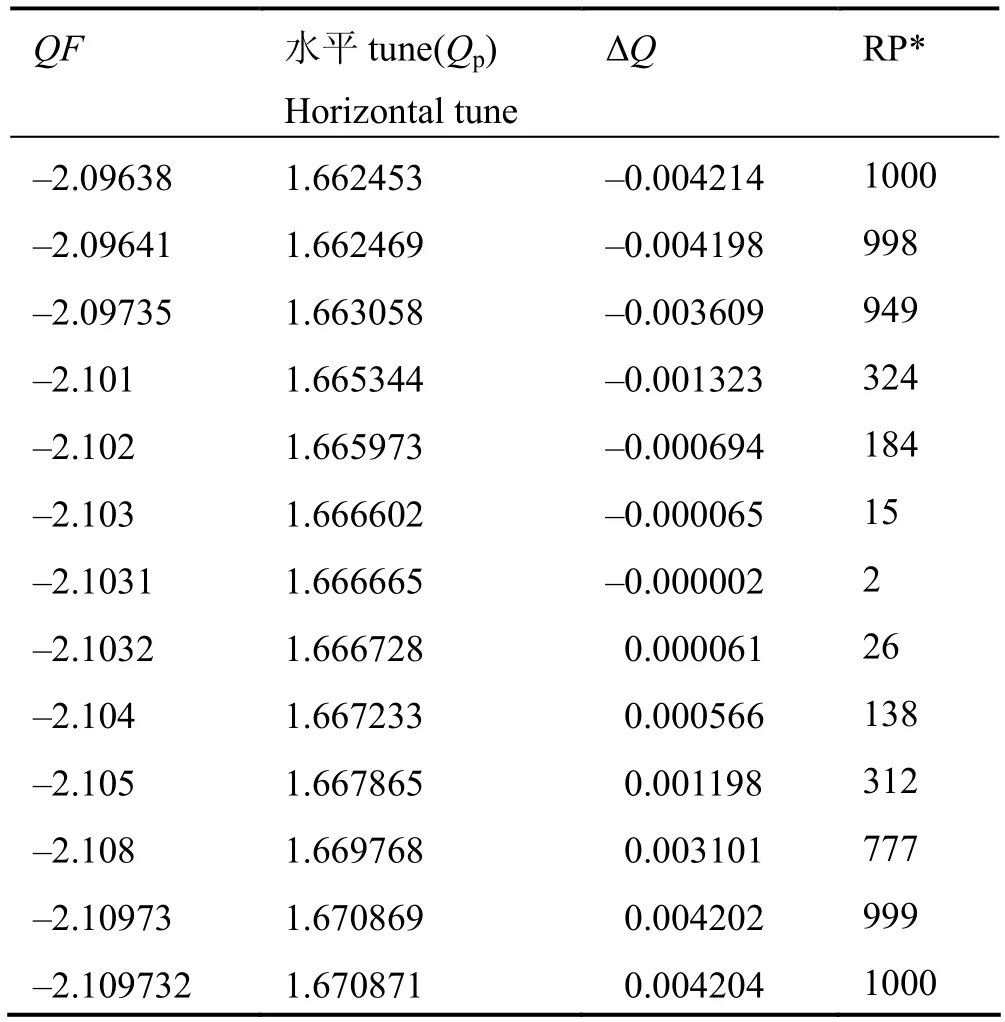
表1 四极磁铁强度变化引起的各参数变化(S不变，总共1000个粒子)Table 1 Parameters under different strengths of the quadrupoles (fixed S, extracted beam of 1000 protons).

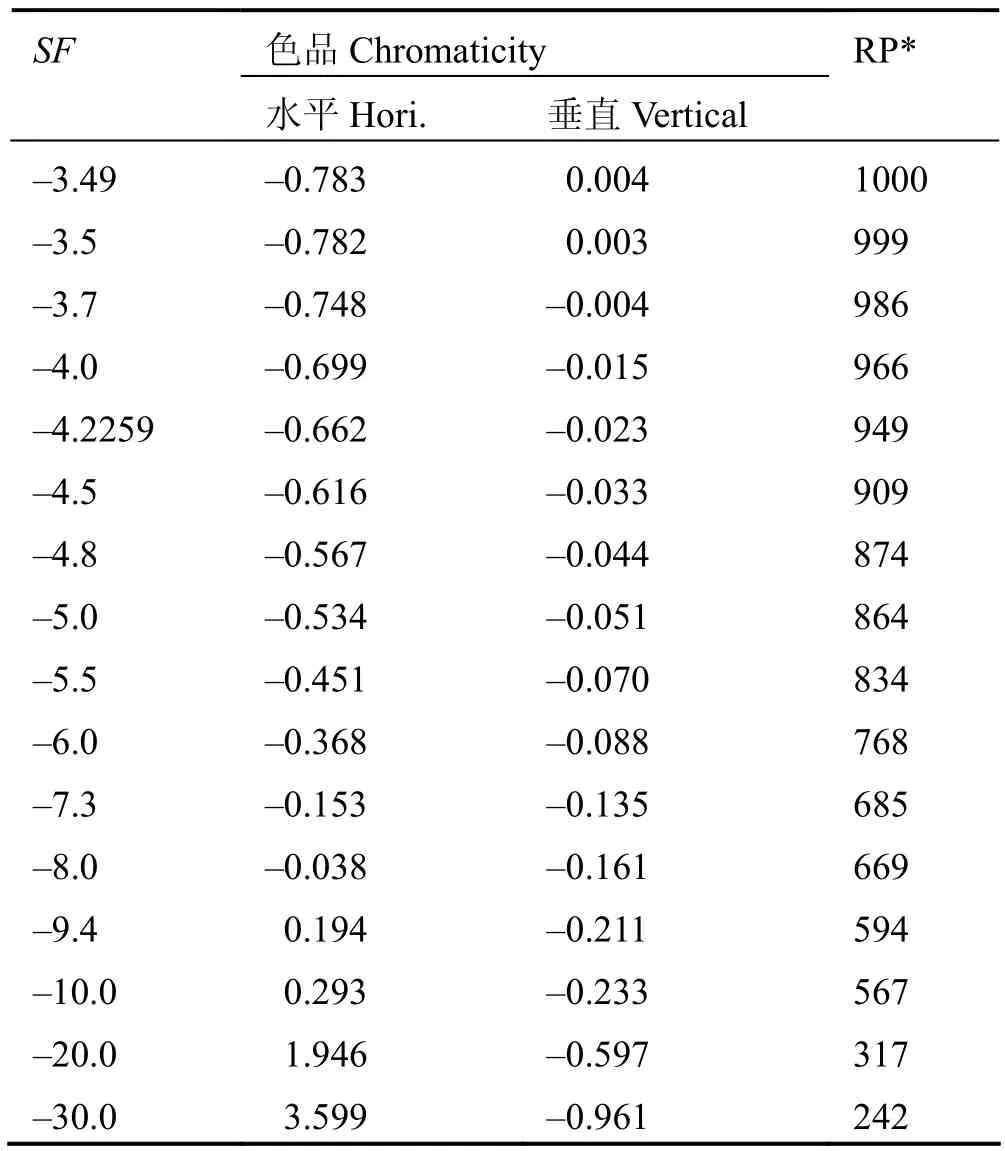
表2 六极磁铁强度变化引起的各参数变化(ΔQ不变，总共1000个粒子)Table 2 Parameters under different strengths of the sextupoles (fixed ΔQ, extracted beam of 1000 protons).

图5 引出粒子的原始曲线与拟合曲线Fig.5 The original curve and fitting curve of extracted particles.

4 结语

应用Hamiltonian理论，分析了医用质子加速器慢引出RFKO方法的基本原理，解析了RFKO方法的振幅增长机制；分析了为使束流幅度达到一定均匀性的幅度调制(AM)函数模型，由此导出不同RFKO踢角和引出束流的关系以及为达到束流均匀引出时踢角随时间变化的关系。

运用软件WinAGILE模拟了初始粒子动量分布与引出束流分布的关系；tune值偏差及共振驱动六极磁铁与引出束流的关系。模拟结果较好验证了理论分析，对医用质子加速器慢引出RFKO调束具有一定指导意义。

1 Sato S, Furukawa T, Noda K. Dynamic intensity control system with RF-knockout slow-extraction in the HIMAC synchrotron[J]. Nucl Instr Meth, A, 2007, 574: 226–231

2 Noda K, Furukawa T, Shibuya S,et al. Source of spill ripple in the RF-KO slow-extraction method with FM and AM[J]. Nucl Instr Meth, A, 2002, 492: 241–252

3 Accelerator complex study group. Proton-Ion Medical Machine Study (PIMMS) Part I [R]. Geneva, 1999

4 刘乃泉. 加速器理论[M]. 第2版. 北京: 清华大学出版社, 2004: 49–58 LIU Naiquan. Accelerator theory[M]. Second ed. Beijing:Tsinghua University Press, 2004: 49–58

5 Noda K, Kanazawa M, Itano A,et al. Slow beam extraction by a transverse RF field with AM and FM[J].Nucl Instr Meth, A,1996, 374: 269–277

6 Furukawa T, Noda K, Muramatsu M,et al. Global spill control in RF-knockout slow extraction[J]. Nucl Instr Meth, A, 2004, 552: 196–204

7 Bryant P J. AGILE program for synchrotron lattice design[OL]. http: //nicewww.cern.ch/～bryant