三个基本初等区间函数的研究

高德宝

（黑龙江八一农垦大学理学院数学系，大庆163319）

区间分析（又称区间计算、区间数学）理论是定义在区间数集上的数学理论。区间分析思想很早以前就出现于文献［1，2］等中，公认的区间分析理论的奠基人是美国数学家Ramon E.Moore。他和R.Baker Kearfott，Michael J.Cloud 三人在 2009年发表了专著《区间分析导论》[3]。区间分析理论已经广泛地应用于科学计算和工程领域，如文［4，5，6，7］。

Moore 在文［3］中对以区间数为变量的初等函数做了很大程度上的论述。特别是对单调函数，如对数函数、指数函数、正弦函数等。由于区间数是由两个区间端点来确定的，故可以说区间数变量是实数域上的二维变量。而Moore 在同一个平面上表述了函数的像与原像之间的关系，在这种情形下，难发现与找到映射的几何性质以及函数本身所固有的一些性质。由于区间数是由两个量来确定的，故从实数意义上来讲，区间数函数应该是由两个变量确定的两个函数。所以区间函数应该是二维空间到二维空间上的映射。从这个角度出发，本文具体的探索了有关区间数函数的概念、计算、映射及其性质。

1 区间数的基本概念及其运算

定义 1 称 A=［al，ar］={x｜al≤x≤ar，x∈R}为一个区间数。当al=ar时，区间数退化为一实数。所有区间数的集合记为I（R）。

定义 2 给定两个区间数 A=［al，ar］，B=［bl，br］。有如下区间数之间的四则运算运算：

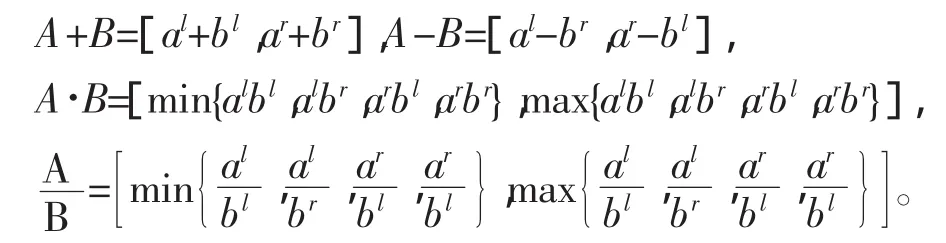
在除法中，应假设0∉B。

上面所提及的理论基本上来源于文献［3，9］。

注1：集合I（R）内的元素与半平面{（x，y）｜x≤y，x∈R，y∈R}内的点具有一一对应关系。

习惯上，我们用［x，y］表示实数域上的闭区间，（x，y）表示平面内的点。本文对闭区间［x，y］（∈I（R））与点（x，y）（x≤y）不作任何区别。

定义 3 设［x1，y1］，［x2，y2］是两个区间数。若 x1=x2，y1=y2，我们则称这两个区间数相等。记作［x1，y1］=［x2，y2］。

注2：本文用I（R）表示实数集R 上的所有闭区间的集合。例如：I（［2，3））表示区间［2，3）上所有闭区间的集合。

2 区间函数

所谓区间函数就是以区间数为自变量与因变量的函数。下面本文给出了一种具体的定义方式。

定义4 如图1 所示，设D，E≤I（R），若对于任意的［x，y］∈D，按照某一法则 f，有唯一的区间数［u，v］∈E 与之对应，则称f 是区间函数。其中D 称为定义域，与D 对应的所有［u，v］的集合称为f 的值域。有时，我们也称这个［u，v］是［x，y］的象，称［x，y］是［u，v］的一个原象。用数学符号把它表达出来就是：

［u，v］=f（［x，y］）。

形如一元实函数，有些区间函数具有一些特殊的性质，比如说奇偶性、周期性、单调性、有界性等。本文仅涉及单调性，下面我们具体阐述区间函数单调性的定义。

在一元函数中，一些函数具有单调性的特性。而区间函数是多元函数，又因为区间数［x，y］本身与具有全序关系的实数不同，不具有自然的全序关系，故一般的情况下无法讨论它们的单调性。但有许多文献（如［8，9］等）讨论了区间数的偏序关系，我们可以在某个序关系下研究区间数函数的单调性。本文着重讨论下面文［3］中偏序关系下的单调性。

定义5 在I（R）中任取两个区间数［x1，y1］，［x2，y2］若 x1≤x2，y1≤y2，我们则称［x1，y1］在［x2，y2］之前，或［x2，y2］在［x1，y1］之后。

这个偏序关系，我们用“≤”来表示。这样，如果［x1，y1］在［x2，y2］之前，那么［x1，y1］≤［x2，y2］。

定义6 设f 在区间数集D 上有定义。我们说

（1） 如果对于D 上的任意两个区间数［x1，y1］，［x2，y2］，当［x1，y1］≤［x2，y2］时，有f（［x1，y2］）≤f（［x2，y2］），我们说f 在D 上是单调递增的。

（2）如果对于 D 上的任意两个区间数［x1，y1］和［x2，y2］，当［x1，y1］≤［x2，y2］时，有f（［x1，y2］）≤f（［x2，y2］），我们说f 在D 上是单调递减的。

注3：由于实数是区间数的特殊情形，故基本初等区间函数定义的基本原则是：当区间数退化为实数时，基本初等区间函数就是基本初等实函数。

2.1 区间指数函数和区间对数函数

定义 7 任取［x，y］∈I（R），对于任意的 t∈［x，y］，有指数函数at（a＞0，a≠1）使得at∈［u，v］∈I（（0，+∞）），同时对于任意的w∈［u，v］∈I（（0，+∞）），存在t∈［x，y］，使得 w=at。从而对于任意的区间数［x，y］∈I（R），按照实数指数函数at的对应法则，存在区间数［u，v］∈I（（0，+∞））与之对应。区间数之间的这种函数关系，我们称其为区间指数函数。记作

［u，v］=a[x，y]。

定理1 设a[x，y]在I（R）上有定义。

（1）当 0＜a＜1 时，a[x，y]=［ay，ax］；

（2）当 a＞1 时，a[x，y]=［ax，ay］。

证明 当0＜a＜1 时，由于at 是单调递减的连续函数，故当 t∈［x，y］时，at∈［ay，ax］。

同时当 w∈［ay，ax］，存在 t∈［x，y］，使得 at=w。故

a[x，y]=［ay，ax］。

同理，当a＞1 时，由于at 是单调递增的连续函数，故 a[x，y]=［ax，ay］。

定理2 设I（R）具有偏序关系“≤”。

（1）当 0＜a＜1，区间指数函数 a[x，y]是单调递减的；

（2）当 a＞1 时，区间指数函数 a[x，y]是单调递增的。

证明当0＜a＜1 时，在I（R）中任取两个区间数［x1，y1］，［x2，y2］且假设 x1≤x2，y1≤y2。

由于 a［x1，y1］=［ay1，ax1］，a［x2，y2］=［ay2，ax2］ 且 ay1≥ay2，ax1≥ax2，故有

［ay1，ax1］≤［ay2，ax2］。

根据定义6 有：指数函数a[x，y]是单调递增的。

同理可证当 0＜a＜1，区间指数函数 a[x，y]是单调递减的。

易知at（a＞0，a≠1）的自然定义域为I（R）。因为ax＞0，所以 u＞0。指数函数［u，v］=a[x，y]将 xy 平面上的集合I（R）映射到uv 平面上的集合{（u，v）｜0＜u≤v，u∈R，v∈R}（见图1）。

当a=e 时，指数函数也可以表示为［u，v］=exp（［x，y］）。

类似于指数函数，我们可以在I（（0，+∞））和I（R）之间定义区间对数函数。记作

［u，v］=loga（［x，y］）（a＞0，a≠1）。

类似于定理1 与定理2 的证明过程，我们可证得以下两个关于区间对数函数的定理。

定理3 设loga（［x，y］）在I（（0，+∞））上有定义。

（1）当0＜a＜1 时，loga（［x，y］）=［logay，logax］；

（2）当a＞1 时，loga（［x，y］）=［logax，logay］。

易知loga（［x，y］）的自然定义域为I（（0，+∞））。故对数函数［u，v］=loga（［x，y］）将xy 平面上的集合I（（0，+∞））映射到uv 平面上的集合I（R）（见图2）。

定理4 设在I（（0，+∞））中具有偏序关系“≤”。

（1）当0＜a＜1 时，区间对数函数loga（［x，y］）是单调递减的；

（2）当a＞1 时，区间对数函数loga（［x，y］）是单调递增的。

当 a=e 时，指数函数也可以表示为［u，v］=ln（［x，y］）。

比较图2 与图3 知：对数函数的原象，象所形成的图形分别与指数函数函数的象，原象所形成的图形是相同的。从这个意义上来讲，对数函数与指数函数是互逆的。

2.2 区间幂函数

定义8 设D，E⊆I（R）。任取［x，y］∈D，对于任意的t∈［x，y］，有幂函数ta（a∈R）使得ta∈［u，v］∈E，同时对于任意的 w∈［u，v］∈E，存在 t∈［x，y］，使得w=ta。从而对于任意的区间数［x，y］∈D，按照幂函数ta的对应法则，存在区间数［u，v］∈E 与之对应。区间数之间的这种函数关系，我们称其为区间幂函数。记作

［u，v］=［x，y］a。

设幂函数 ta在闭区间［x，y］上有定义，则 ta 在［x，y］上连续。从而ta的值域为

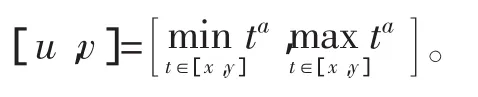
从而幂函数的具体计算公式为

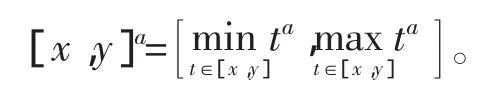
上面的计算公式对所有区间幂函数都是成立的，下面讨论几种特殊情形。根据实数幂函数的定义以及幂函数的连续性，易知有下面的结论。

定理 5 设［x，y］a是区间幂函数，则

（1）当 a≥0，x∈［0，+∞］时，［x，y］a=［xa，ya］。

（2）当 a＜0，x∈（0，+∞）时，［x，y］a=［ya，xa］。

（3）当a=n 是正整数时，有

上式给出了当x∈［0，+∞］时，区间幂函数比较简明的计算公式。但若 y∈（-∞，0） 或 0∈（x，y），当x=y 时，［x，y］a在实数域内可能无意义。考虑到这种情形，我们需要下面的引理。

引理1 设实数幂函数ta在（-∞，0）上有定义，则

证明 当t＜0 时，根据有关复数理论[10]，我们有

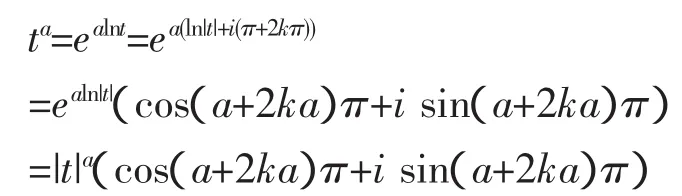
上式结果为实数的充分必条件是（a+2ka）π=mπ（m，k=0±1，±2，…），即

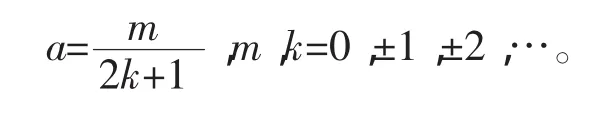
在这种情形下，

ta=｜t｜acos（mπ）=（-1）m｜t｜a=±｜t｜a，m=0，±1，±2，…。利用引理1 以及函数ta的单调性，容易证明下面定理6 的结论。

定理 6 设［x，y］a在 I（（-∞，0））上有定义和 t＜0。

（1）如果 ta=｜t｜a且 a＞0，那么［x，y］a=［ya，xa］；

（2）如果 ta=｜t｜a且 a＜0，那么［x，y］a=［xa，ya］；

（3）如果 ta=-｜t｜a且 a＞0，那么［x，y］a=［xa，ya］；

（4）如果 ta=-｜t｜a且 a＜0，那么［x，y］a=［ya，xa］。

3 总结

本文在给出区间数函数定义的基础之上，定义了基本初等区间指数函数、区间对数函数和区间幂函数。并进一步的讨论了这些函数的一些固有性质。其次，以区间对数函数和区间指数函数的自然定义域和值域分别为原象和象，在两个平面上给出了这两个函数的映射图形。

［1］ R.C.Young.The algebra of many-valued quantities［J］.Math Ann，1931，104:260-290.

［2］ T.Sunaga.Theory of an interval algebra and its application to numerical analysis［J］.AAG Memoirs，1958，2:547-564.

［3］ R.E.Moore，B.Lodwick，M.J.Cloud.Introduction to interval analysis［M］.Society for Industrial and Applied Mathematics Philadelphia，2009.

［4］ E.R.Hansen.On solving systems of equations using interval arithmetic ［J］.Mathematics of Computation，1968，22:81-87.

［5］ L.jaulin，S.Ratschan，L.Hardouin.Set computation for nonlinear control［J］.Reliable Computing，2003，9:81-87.

［6］ L.Jaulin.Reliable minimax parameter estimation［J］.Reliable Computing，2001，7:231-246.

［7］ D.Henrion，O.Bachelier.Low-order robust controller synthesis for interval plants［J］.International Journal of Control，2001，74:1-9.

［8］ S.Chanas，P.Zielinski.Ranking fuzzy interval numbers in the Setting of random sets-further results［J］.Information Sciences，1999，117:201-207.

［9］ A.Seqngupta，T.K.Pal，On comparing interval numbers［J］.European Journal of Operation Research，2000，127:28-43.

［10］ S.Lange，Complex analysis ［M］.Springer-Verlag New York，Inc.1999.