某型机载电子设备无失效数据可靠性研究＊

曲晓燕 吕晓峰 李小晨

（1.海军航空工程学院兵器科学与技术系 烟台 264001）（2.徐州空军学院航空弹药系 徐州 221000）

1 引言

一般而言，电子设备的可靠度与其通电时间是密切相关的，大量的历史统计数据表明，大部分电子设备的“通电时间寿命”均服从指数分布［1～2］，因此可以将机载电子设备通电时间寿命的分布当作指数分布处理，即：

f（t）＝λexp（－λt），t＞0，0＜λ＜＋∞ （1）其中λ为失效率。对于样本量较大，并且寿命试验过程中出现失效样本的情形，寿命分布模型及参数估计的相关理论已经比较成熟。可靠度方面的相关理论已经有较为成熟的处理方法［3～4］。但随着机载电子设备可靠性的提高，经常会出现寿命试验过程中没有失效样本的情况，但这并不意味着设备的可靠度为1，需要在一定置信度水平下合理评估设备的可靠性水平，此时的处理方法与传统方法有较大的差异［5～6］。当已经确定产品寿命服从指数分布时，传统的可靠性理论通常根据样本失效时间及数量，对失效率作极大似然估计，进而估计产品的可靠度；对于无失效数据时的情况，本文提出了一种基于失效率上限已知的Bayes产品可靠度估计方法。

2 失效率相关信息未知时的处理方法

对于寿命服从指数分布的产品，当进行定时截尾寿命试验未出现失效样品时，在1－α置信水平下，其最优可靠度置信下限为［7］

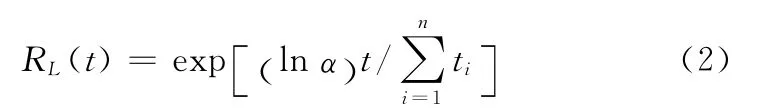
这里将某型机载电子设备出现不可修复故障定义为失效。在监控使用的条件下，n部该型电子设备经过一定的通电时间后均未出现不可修复故障。因此对于这n部设备而言，该监控使用过程属于无失效样品的定时截尾寿命试验。实际一共有13部设备，因此试验次数n＝13，每次试验的样品个数为1，试验的截尾时间即设备的通电时间（小时）如下：

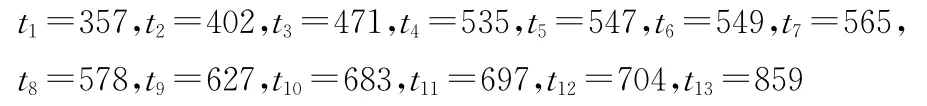
根据式（2）可以求得该型机载电子设备通电时间为t时，置信水平为1－α＝1－0.1＝0.9的最优可靠度下限。该型机载电子设备的可靠度随通电小时数的变化趋势如图1所示。

该型机载电子设备的通电可靠度在整个使用期内服从指数分布。但因为设备的可靠性水平非常高，其寿命分布中的失效率参数值很小，所以在较短的时间范围内可靠度与通电时间近似呈线性关系。

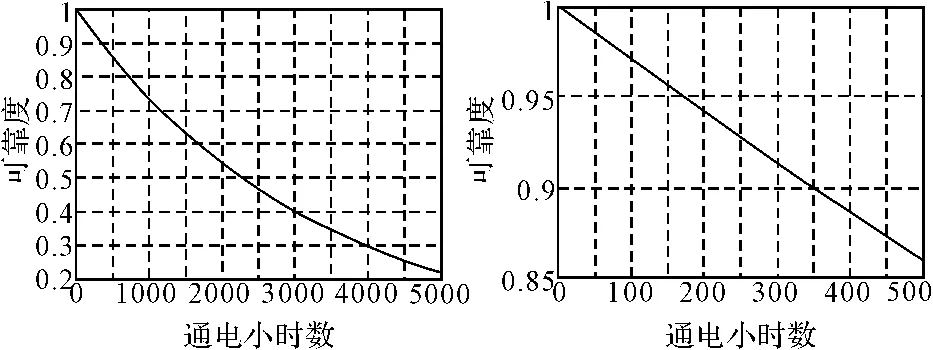
图1 机载电子设备可靠度

3 基于Bayes理论的估计方法

采用Bayes方法结合失效率的上限值分析设备的可靠性可以有效地利用先验信息（通电寿命服从指数分布和失效率的上限值）和后验信息（通电小时数），进而提高该型机载电子设备可靠度的预测精度。

在无失效数据的情形下，失效率λ不会很大，若能根据先验信息给出λ的一个比较保守的上限λ0（即0＜λ＜λ0，其中0＜λ0＜＋∞），则可以有效地提高产品可靠性预测精度。如果只知道0＜λ＜λ0，而其它一无所知，不妨取（0，λ0）上的均匀分布作为λ的先验分布，其概率密度函数为：π（λ）＝1／λ0，其中0＜λ＜λ0。

对寿命服从指数分布的产品进行n次定时截尾试验，每次试验截尾时间为ti，（i＝1，2，…，n），t1＜t2＜…＜tn，与之相对应的样品数为mi（i＝1，2，…，n），结果所有样品无一失效，获得的无失效数据为（ti，mi），i＝1，2，…，n。若λ的先验概率密度为π（λ）＝1／λ0，则λ的置信水平为1－α的Bayes置信上限估计［8～9］为

式（3）成立的证明［10］如下：

对寿命服从指数分布的产品进行n次定时截尾寿命试验，若第i次试验的mi个样品中有Xi个样品失效，则Xi服从参数为mi和p的二项分布B（mi，p），其中p＝∫ti0λexp（－λt）dt＝1－exp（－λti），对于无失效的情况，失效率λ很小，所以ti不太大时，λti→0，忽略高阶无穷小有p＝1－exp（－λti）≈λti。根据泊松定理，可用泊松分布逼近二项分布，因此Xi的分布近似的服从参数为mitiλ的泊松分布，则有：

若每次截尾试验是相互独立的，则λ的似然函数：

对于无失效情况，即ri＝0时，则有：

根据 Bayes定理，λ的后验密度［11，13］为

其中0＜λ＜λ0。在1－α置信水平下，λ的Bayes置信上限λU应满足p（λ≤λ0）＝1－α，即：

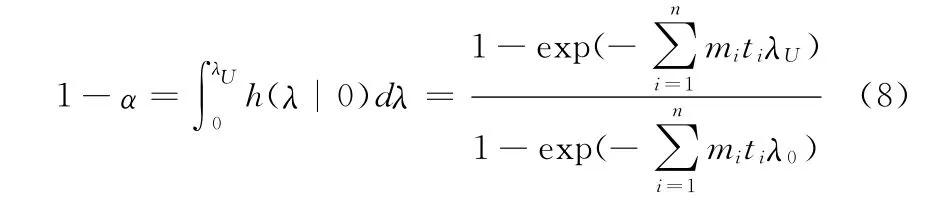
解得：

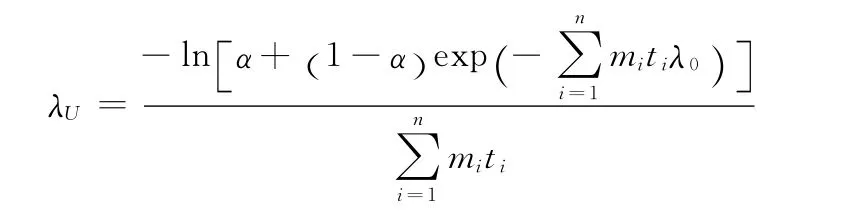
4 已知失效率上限时的可靠性评估

采用Bayes方法估计该型机载电子设备的可靠性，首先要估计出失效率λ的上限λ0。该设备生产研制单位给出的可靠性指标为：无故障完成100次挂飞任务的概率不小于95%。设备在此期间内的通电总时间T≈250h，则设备在T时刻最低的可靠性R（T）＝0.95，即exp（－250λ0）＝0.95，λ0＝2.05×10－4／h。

在监控使用的条件下，13部设备均未出现不可修复故障。因此该监控使用过程属于无失效样品的定时截尾寿命试验。试验次数n＝13，每次试验的样品个数为1即mi＝1，试验的截尾时间即设备的通电时间（小时）如下：

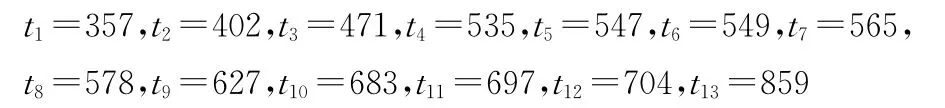
在1－α＝1－0.1＝0.9置信水平下，根据式（3），求得λU＝1.63×10－4。

则该型机载电子设备的可靠度下限为R（t）＝exp（－λUt）＝exp（－1.63×10－4t），将设备的可靠度随通电时间的变化趋势列于表1。

5 两种可靠性评估方法的比较

为便于比较分析，将该型机载电子设备的两种可靠性评估方法：基于指数分布的可靠性评估（方法Ⅰ）和基于Bayes估计的可靠性评估（方法Ⅱ）的结果绘于图2。

从图2可以看出：

该型机载电子设备的通电时间可靠度服从指数分布，但在比较短的时间段内其可靠度与通电时间近似呈线性关系。

方法Ⅰ求得的可靠性下限值偏小，这是因为方法Ⅰ只利用了通电寿命服从指数分布这一信息，而对于失效率λ的分布形式和失效率λ上限均没有考虑，故求得结果过于保守。

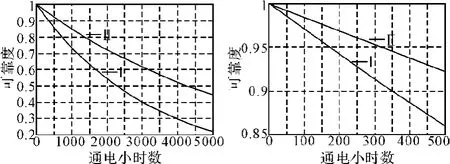
图2 不同评估方法得到的可靠性水平

方法Ⅱ求得的可靠性下限值较方法Ⅰ的结果要大，这是因为方法Ⅱ不仅利用了通电寿命服从指数分布这一信息，而且还考虑了失效率λ的上限λ0，故求得的结果更接近于实际情况。

在进行无失效数据可靠度估计时，如果只知道设备可靠度服从指数分布而失效率λ上限未知时，应在一定置信水平下采用方法Ⅰ估计设备的可靠度下限。如果已知设备可靠度服从指数分布，并且已知失效率λ上限，应在一定置信水平下采用方法Ⅱ估计设备的可靠度下限，此时求得的结果要优于方法Ⅰ。

6 结语

机载电子设备可靠度高，常常需要在无失效数据的情况下分析其可靠性水平，传统的分析方法已不适用。本文提出的方法是根据机载电子设备通电使用寿命服从指数分布的特点，采用基于贝叶斯理论的无失效数据处理方法，在一定置信水平下评估它们的通电可靠度。该方法考虑了设备的失效率上限，因而具有较高的精度，可以为确定该型机载电子设备使用寿命提供依据，并能够为制订合理的维修资源提供理论依据。

［1］中国人民解放军总装备部.试验数据的统计分析［M］.北京：国防工业出版社，2002：233－234.

［2］李正，宋保维，毛昭勇.无失效指数分布参数的模糊加权最小二乘估计［J］.系统仿真学报，2005，6（17）：1373－1375.

［3］曹晋华，程侃.可靠性数学引论［M］.北京：高等教育出版社，2006：365－405.

［4］石颉，谌登华，施海宁，等.核电站仪控开关可靠性数据分析与处理［J］.核动力工程，2010，2（31）：54－58.

［5］李亿民.关于指数分布无失效数据的一种Bayes分析［J］.山东理工大学学报，2006，（20）3：17－19.

［6］韩明.可靠性参数的M－Bayes可信限［J］.系统工程与电子技术，2008，8（30）：1592－1594.

［7］贺国芳.可靠性数据的收集与分析［M］.北京：国防工业出版社，1995：95－96.

［8］韩明.无失效数据情形可靠性参数的置信限［J］.工程数学学报，2004，（21）4：206－210.

［9］韩明.产品无失效数据的综合处理［J］.机械工程学报，2003，2（39）：129－132.

［10］韩明，丁元耀，陈涛.指数分布无失效数据的多层Bayes分析［J］.数理统计与管理，1998，（4）7：205－208.

［11］范金城，吴可法.统计推断导引［M］.北京：科学出版社，2001：113－115.

［12］罗勇，夏丹，徐丹.基于可靠性评估的维修诊断辅助决策系统研究［J］.计算机与数字工程，2011（11）.

［13］韩明.基于无失效数据的可靠性参数估计［M］.北京：中国统计出版社，2005：143－144.