基于主成分分析的高校学生体质状况研究

华冬芳，武 斌

（无锡科技职业学院，江苏 无锡 214028）

基于主成分分析的高校学生体质状况研究

华冬芳，武 斌

（无锡科技职业学院，江苏 无锡 214028）

论文依托无锡科技职业学院2010级、2011级高职学生的体质测试数据，运用主成分分析法，得出学生体质的主要影响因素及影响程度，寻求学生体质差异的主要原因，为高校有效地指导大学生锻炼身体提供坚实基础。

主成因分析；大学生；体质

2010年国民体质监测公报结果表明，我国国民体质的总体合格率呈现持续上升的态势，中小学生的身体素质也有效改善，但我国大学生的身体素质仍在继续缓慢下降。有专家表明，一方面与他们在高中期间忽视体育锻炼或体育锻炼不做有着直接关系，高考的压力直接影响了学生必需要进行的体育锻炼，导致学生素质的下降；另一方面，大学生对体育锻炼的意义、方式方法认识不足，加上现在很多大学体育教育都采取体育俱乐部形式，缺乏科学的体育指导和运动知识的普及，从而导致大学生的身体素质得不到全面、均衡、有效的锻炼和提高。在此背景下，了解高校学生的体质状况，有的放矢地指导他们进行科学有效的体育锻炼，是当前高校体育工作刻不容缓的一部分。

在高校学生的体质综合评价中，评价指标的选择以及权重的确定往往带有较强的主观意愿。在加权法中，各评价指标的客观性较差；专家咨询法得到的权重因子也具有不确定性和模糊性；层次分析法虽然采用较为精确的数学方法来计算权重，但判断各因素的定性成分居多，主观因素仍较大。但各指标的权重对学生体质评价的影响却很大，论文试图采用主成分分析法，将多个指标整合成少数几个综合指标，但保持原有指标所涵盖的信息量来分析得出影响学生体质的主要影响因素及其影响程度，科学有效地指导大学生进行身体锻炼。

一、指标、方法及数据说明

1.指标说明

论文选取的指标变量主要依据是《大学生体质健康标准》中重要的体质考核测试项目：身高（x1）、体重（x2）、肺活量(x3)、耐力类项目(x4)、柔韧、力量类(x5)、速度、灵巧类(x6)六个变量。

2.分析方法

主成分分析（principal component analysis，简称PCA）是由霍特林（Hotelling）于1933年首先提出的。它是一种通过数据降维技术把多个变量化为少数几个主成分的统计分析方法。

由于许多变量之间往往存在着一定程度的相关性，导致增加问题分析的复杂性，而盲目地减少变量则会损失很多信息，人们自然就希望通过线性组合的方式，在损失较少数据信息的基础上把多个指标转化为几个有代表意义的综合指标，而这些综合指标之间彼此不相关、信息不重叠，这就是主成分分析的思想，通过主成分既可以降低数据“维数”，又保留了原数据的大部分信息。

3.数据说明

论文所用数据样本为无锡科技职业学院2010级和2011级学生（合计4858人）的体质健康测试数据，测试时间为2011年11月。

二、实证分析结果

1.适应性检验及主成分选取

首先对样本数据进行主成分分析适合性检验，运用SPSS17.0软件进行巴特利（Bartlett）球形检验统计量的观察值为11604.3，相应的概率P值接近0，在a=0.01水平上显著。同时，KMO检验系数为0.809，根据Kaiser给出的KM0度量标准大于0.5可知，样本数据很适合进行主成分分析。

将前述数据代入SPSS17.0进行标准化处理，得出相关系数矩阵，求解相关矩阵的特征值，并根据累计贡献率在一个较好的百分比（80%-90%）标准内，从六个变量中提取四个主成分因子，进行主成分分析。

从表1中可以看到，四个主成分因子的累计贡献率达到了89.658%，表明了这四个主成分因子包括了6个变量的大部分信息总量，很好地概括了原始变量，即这4个主成分显著地反映了该校大学生体质健康状况。（见表1）

2.主成分因子旋转及解释

为了使每个主成分因子在不同原始变量上的载荷有明显的差别，借助旋转技术，旋转调整初始因子载荷矩阵，将同一因子较高载荷的评价指标排列在一起，得到旋转后的因子矩阵，更便于解释因子，如表2所示。

（1）主成分1(以F1表示)在身高（x1）、肺活量（x3）、速度、灵巧类项目（x6）三个方面皆有很高的载荷系数，反映的是大学生身体的基本成长发育状况，称第一主成分为“成长因子”。

（2）主成分2（以F2表示）在体重（x2）方面有很高的载荷系数，在身高（x1）方面也有中等程度的载荷系数，第二主成分反映的是大学生的“胖瘦状况”，可称为“胖瘦因子”。

（3）主成分3（以F3表示）在柔韧、力量类项目（x5）方面有很高的载荷系数，它反映的是大学生的“柔韧性状况”，称为“柔韧性因子”。

（4）主成分4（以F4表示）在耐力类项目（x4）方面有很高的载荷系数，而在其余变量上的载荷都很小，它反映的是学生的耐力状况，可以称为“耐力因子”。

3.评价结果

为了计算主成分因子的得分，利用回归法将主成分对指标变量做线性回归，得到系数的最小二乘估计，即成分得分系数。根据成分得分系数，可以得到主成分F1、F2、F3、F4的得分模型。

F1=0.522x1-0.393x2+0.443x3-0.109x4-0.413x5+0.644x6

F2=0.179x1+0.969x2+0.024x3+0.079x4+0.027x5-0.482x6

F3=-0.457x1+0.064x2-0.143x3-0.017x4+1.152x5+0.051x6

F4=-0.002x1+0.048x2-0.037x3+1.014x4-0.009x5-0.067x6

同时，以旋转后累计方差贡献表中的各成分对应方差贡献率作为各主成分的权重，构造出如下大学生体质状况得分模型：

F=32.259%F1+21.892%F2+18.686%F3+16.82%F4

然后，我们可以根据F的值大小对学生的整体体能进行排序，并指导学生进行针对性的体育锻炼。

三、结论

1.主成分分析法运用于高校学生体质状况分析，可以有效地规避在体质状况研究中各测量指标权重设置的主观因素的影响，再通过选取主成分因子，计算出各成分的贡献率，从而科学地分配各成分因子的权重。

2.在大学生体质健康测试项目数据的四个主成分中，依贡献率大小排序，分别为成长因子（身高、肺活量、速度灵巧类项目）、胖瘦因子（身高、体重）、柔韧性因子（柔韧、力量类项目）和耐力因子（耐力类项目），所以我们在评价体系中应注意考虑和调整相应的权重。

3.根据主成分综合得分值，我们不仅可以对学生体质总体水平的优劣进行排序，并能较为准确地分析出每一个学生体质上的特点与不足，从而达到按个体差异性开具运动健身处方的目的，科学地指导学生进行体育锻炼。

[1]王晓芬.体育统计与SPSS[M].北京:人民体育出版社，2001.

[2]何晓群.多元统计分析[M].北京:中国人民大学出版社，2004.

[3]朱建平.应用多元统计分析[M］.北京:科学出版社，2006．

[4]袁运平.我国男子百米跑一级运动员体能水平的评价与诊断[J].北京体育大学学报，2002，(4):547-549.

[5]谭玉霞，蔡瑞广，董新阳，崔伍增.应用灰色理论对大学生体质因素结构的初步研究 [J].河北体育学院学报，2002，（2）.

[6]董艳国，黄爱武，白海军，自明.基于多元统计分析方法对大学生身体素质的动态分析[J].首都师范大学学报（自然科学版），2007，（6）.

[7]谭磊.湖南理工学院大学生体质健康的测试分析与对策[J].湖南理工学院学报(自然科学版)，2009，（1）.

[8]张亚平，芮飞龙，郭卫.主成分分析法在西北五所高校学生体质测试中的应用[J].甘肃联合大学学报(自然科学版)，2010，（4）.

[9]李进华，缪仕晖.大学生体质与健康标准测试数据结果分析[J].宁德师范学院学报(自然科学版)，2011，（3）.

表1 变量的累计方差贡献率

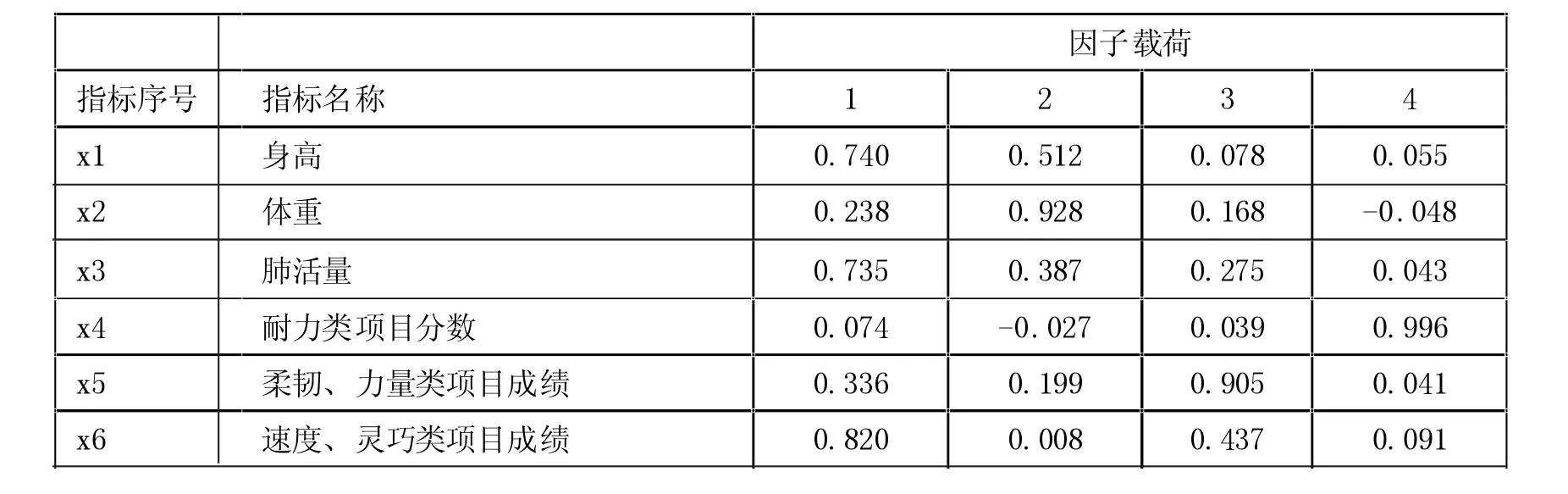
表2 旋转后的因子载荷矩阵

G64

A

1673-0046（2012）6-0160-02

江苏省2010年高等学校大学生实践创新训练项目：《高校学生体质状况调研及有效改善过程的数理建模研究》研究成果(张奇、张龙平等负责数据采集等工作)