金属铌声子发散谱、电声耦合和超导转变温度的研究

陈秋成

（衡阳师范学院 物理与电子信息科学系，湖南 衡阳 421008）

0 Introduction

The solving of many－particle schrödinger equation is a key problem of quantum mechanics.Density functional theory （DFT）［1－2］is a suitable method aiming to this topic.The main idea of DFT is to describe an interacting system of fermions via its density and not via its many－body wave function.For N electrons in a solid，which obey the Pauli principle and repulse each other through the Coulomb potential，this means that the basic variable of the system depends only on three（the spatial coordinates x，y，and z）rather than 3Nde－grees of freedom.Up to now，The DFT method becomes an effective and popular way in description of ground state properties of metals［3，4］.

Many physical properties of metals，such as electrical and thermal resistivity，thermal expansion，and superconductivity，appear to be determined by phonons and their interactions with electrons［5］.To investigate these physical properties，the lattice vibration（phonons）must be first considered.Common ways to calculate phonons are the frozen－phonon approximation［6，7］and the density functional perturbation theory （DFPT）［8，9］.In contrast to the former，DFPT is well established in predicting the phonon dispersion，in which phonons at any wave vector in the Brillouin zone（BZ）are accessible.Therefore，quantities that involve integrations over the phonon dispersion throughout the BZ can be accurately determined.In this paper，we adopt the DFPT to explore the phonon frequencies of metal niobium.

Niobium，a transition metal with a electron configuration［Kr］4d45s1，crystallizes in body－centered cubic （BCC）bravais lattice.Niobium becomes a superconductor at cryogenic temperatures with the highest superconducting transition temperature 9.2K［10］in all metals.By doping，the niobium compounds even have higher superconducting transition temperature.The superconductive properties are strongly dependent on its purity of niobium.In this paper，we use the DFT method for the electronic structure calculations and the DFPT method for lattice dynamics of niobium.Based on the obtained phonon frequencies，the electron－phonon coupling constant and the superconducting transition temperature will be determined at last.

1 Calculational method

The first－principles density functional theory is adopted to perform the electronic structure calculations of niobium.The local density approximation（LDA）parameterized by Perdew［11］and the relativistic analytic pseudopotential of Hartwigsen，Goedecker and Hutter （HGH）［12］are used.The Brillouin zone integral chooses a Monkhorst－Pack（MP）sampling scheme［13］with the characteristic width of the smearing function 0.01eV to obtain the convergence of 10－6eV in energy.The influence of different k－point sampling and plane－wave cutoff energy will be explored in a series of test calculations in next part.Phonon frequencies are calculated from density functional perturbation theory（DFPT）.Dynamical matrices and linearized potentials are calculated in the irreducible Brillouin zone on a 6×6×6q－points mesh using the groundstates wave functions obtained.

2 Results and discussion

The plane wave cutoff energy Ecutand the density of k－point are of importance to all the calculations under pseudopotential plane－wave approximation.Therefore，the suitable values for such two parameters must first be determined.A series of Ecutare set to obtain the total energy.The results are shown in figure 1，from which one can find that the energy decreases gradually with Ecut.From 100to 300eV，the total energy changes steeply.Above 300eV，the energy almost keeps unchanged.The energy difference between 300and 400eV is under 0.0001meV，indicating the cutoff energy of 300eV is enough in describing the wave function expansion.Therefore，we choose 300eV for cutoff energy in all the coming calculations.For k－piont，the test calculations show 12×12×12 MP grid can give a good self－consistent results with the total energy difference under 0.0001meV.

Figure 1 The dependence of total energy on plane－wave cutoff energy Ecut.

We first optimize structure parameters of niobium at zero pressure without any constrains imposed on the lattice.The optimized lattice constant a（orb，c）and bulk modulus B0are 3.29Åand 180 GPa，respectively.The results are of the typical accuracy of local density approximation pseudopotential calculations and are consistent with experimental values［14］and the theoretical results［15］.

The electronic energy band structure and density of state（DOS）are then calculated.They are shown in figure 2（a）and（b）.It can be found that there are energy bands across the Fermi level along every high line in reciprocal lattice Brillouin zone，i.e.，alongΓ－H－N－P－Γ－N line.These bands mainly are occupied by the d electrons of niobium which is responsible for superconductivity of niobium.From DOS，the Fermi energy expresses a high peak，pointing out the DOS is of the typical metals.The calculated band structure and the DOS here is in good agreement with the results by using the augmented－plane－wave（APW）method［16］.

Figure2 Band structure（a）and density of state（b）of niobium.The Fermi energy is set to zero.

As a gateway to the electron－phonon coupling and superconducting properties，the phonon frequencies must be first calculated.The obtained dispersion curve of niobium is shown in figure 3.The trend of the curves is almost same as that by Bauer et al.［15］except for a little difference，which may originate from different pseudopotential between us.Only three acoustic branches are expected.Along H－P－Γ－H direction，two acoustic branches degenerate.The maximum phonon frequency occurs in H point with a value of 6.2THz.The minimum one is atΓpoint，supporting that the center of reciprocal lattice Brillouin zone（BZ）is not vibrational due to the complete symmetry of BZ in body－centered－cubic lattice.No imaginary frequencies are found in the dispersion curve.

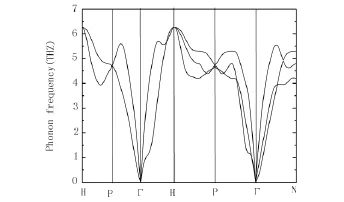
Figure3 The obtained phonon dispersion curve of niobium.

The central quantity is the electron－phonon spectral function or Eliashberg functionα2F（ω）in the theory of superconductivity，which measures the contribution of phonons with frequencyωto scattering processes of electrons at the Fermi level.α2F（ω）can be expressed in terms of the phonon linewidthγqj，

where NFis the density of states at Fermi energyεF.γqjarising from electron－phonon interaction is given by

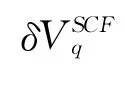
The obtained electron－phonon spectral functionα2F（ω）of niobium are plotted in figure 4 which shows good agreement with another theoretical investigation［15］.It is obvious that three peaks appear in figure 4.They are at 4.05，5.10 and 5.37THz，respectively.The intensity of the last peak is relatively big.The shape of the spectral function common is similar to that of the phonon density of stats（PDOS）and the peaks also appear in the same frequency zone.Therefore，we can safely conclude that the same three peaks appear in the PDOS，indicating that the phonon frequencies of niobium mainly concentrate in the zone arranging from 4.05to 5.37THz.

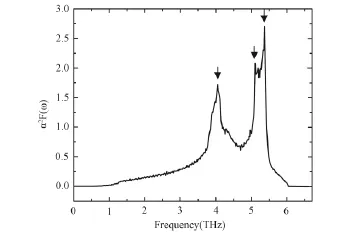
Figure 4 The obtained electron－phonon spectral functionα2 F（ω）of niobium.

The strength of the electron－phonon coupling can be estimated by the electron－phonon coupling constantλdefined as

The obtainedλin this work（1.24）is close to the experimental value of 1.22［17］and the theoretical value of 1.32［15］.There are three independent ways to determineλ.The first is from the observed mass.The second is from the density of state at Fermi surface［18］.A third method is based the from superconductivity theory at present，which can gives reliable results independent of the knowledge of the potential.

Finally，we discuss the superconducting transition temperature Tcof niobium.In McMillan's theory［10］，the Tccan be calculated by the following expression

whereωlogis the logarithmic average frequency.μ＊is the Morel－Anderson pseudopotential representing Coulomb repulsion.kBis the Boltzmanns constant.This equation yields values of Tcwhenλ，μ＊andωlogare all known.ωlogis easily obtained from the phonon frequencies.In practice，μ＊is not usually known，but a rough estimate is adequate because Tcis not too sensitive to it，unlessλis fairly small［18］.Finally，Tcof niobium can be determined by the formula above.Usingμ＊＝0.085，we induce that Tc＝9.16K.It is close to the value of 9.22K［10］.

3 Conclusion

In summary，the first－principles density functional theory together with plane wave pseudopotential methods are applied to investigate the electronic structure，lattice vibration and then the superconducting properties of niobium.The relativistic analytic pseudopotential of Hartwigsen，Goedecker and Hutter（HGH）are adopted.The equilibrium lattice constant，bulk modulus，electronic energy band structure，phonon dispersion are given.Based on the calculated the phonon frequencies，the electron－phonon coupling constantλare determined to be 1.22，Using the McMillan equation，we obtain the superconducting transition temperature Tc＝9.16K.The results presented in this paper agree well with available experimental and theoretical data，supporting the HGH pseudopotential is suitable for the simulations in electronic，vibrational，and superconducting properties of niobium.

［1］Kohn W.Nobel Lecture：Electronic structure of matter：wave functions and density functional［J］.Rev.Mod.Phys.，1999，71：1253－1266.

［2］Hohenberg P，Kohn W.Inhomogeneous Electron Gas［J］.Phys.Rev.，1964，136：B864－B871.

［3］Deng X H，Lu W，Hu Y M，et al.The elastic properties of hexagonal osmium under pressure：The first－principles investigations ［J］.Physica B，2009，404：1218－1221.

［4］Deng X H，Wang W W，Zhang D Y，et al.Detailed investigation of thermodynamic properties of hexagonal osmium using the ab－initio technique ［J］.Physica B，2011，406：656－662.

［5］Kittel C.Quantum Theory of Solids［M］.New York：John Wiley ＆Sons，1963.

［6］Furthmüller H，Kresse G，Hafner J.Ab initio force constant approach to phonon dispersion relations of diamond and grapheme ［J］.Europhys.Lett.，1995，32：729.

［7］Alfe D，Price G D，Gillan M J.Thermodynamics of hexagonal－close－packed iron under Earth's core conditions［J］.Phys.Rev.B，2001，64：045123－045138.

［8］Baroni S，Giannozzi P，Testa A.Green's－function approach to linear response in solids［J］.Phys.Rev.Lett.，1987，58：1861－1864.

［9］Baroni S，Corso A D，Giannozzi P，et al.Phonons and related crystal properties from density－functional perturbation theory ［J］.Rev.Mod.Phys.，2001，73：515－562.

［10］McMillan W L.Transition te1nperature of strong－coupled superconductors［J］.Phys.Rev.，1968，167：331－344.

［11］Perdew J，Zunger A.Self－interaction correction to den－sity－functional approximations for many－electron systems［J］.Phys.Rev.B，1981，23：5048－5079.

［12］Hartwigsen C，Goedecker S，Hutter J.Relativistic separable dual－space gaussian pseudopotentials from H to Rn［J］.Phys.Rev.B，1998，58：3641－3662.

［13］Monkhorst J，Pack J D.Special points for brillouinzone integrations［J］.Phys.Rev.B，1976，13：5188－5192.

［14］Hellwege K H，Madelung O.Structure Data of Elements and Intermetallic Phases ［M ］.Berlin：Springer，1971.

［15］Bauer R，Schmid A，Pavone P，et al.Electron－phonon coupling in the metallic elements Al，Au，Na，and Nb：A first－principles study［J］.Phys.Rev.B，1998－Ⅱ，57：11276－11282.

［16］Mattheiss L F.Electronic structure of niobium and tantalum ［J］.Phys.Rev.B，1970，1：373－380.

［17］Bostock J，Diadiuk V，Cheung W N，et al.Does strong－coupling theory describe superconducting Nb？［J］.Phys.Rev.Lett.，1976，36：603－606.

［18］Allen P B，Cohen M L.Pseudopotential calculation of the mass enhancement and superconducting transition temperature of simple metals［J］.Phys.Rev.，1969，187：525－538.