基于局域波及相关性分析的滚动轴承故障诊断✳

崔宝珍,潘宏侠,王泽兵

(中北大学 机械工程与自动化学院 ,山西 太原 030051)

滚动轴承是旋转机械中应用最为广泛的机械零件,也是最易损坏的元件之一.旋转机械的许多故障都与轴承有关,而从运行尤其是故障发生发展过程中的工程设备上测得的动态信号,其平稳性是相对的、局部的,非平稳性则是绝对的、全局的甚至是广泛的.如何从测得的动态信号中提取故障特征,及时准确地找出故障源,避免重大事故的发生,是一个急待解决的问题,也是机械故障诊断技术进一步深入发展所面临的重大课题之一.

局域波法[1]是 2000年马孝江教授通过对非平稳信号内在特征的深入分析,结合 Huang的思想和 EMD算法,发展起来的一种全新的信号分析方法.它的出现把繁杂的信号分析方法分为局域波法和全域波法.所谓全域波法是指在信号分析中信号频率的定义是基于分析数据整个时间历程上;而局域波法信号频率的定义是基于波形的局部特征及瞬时特征,从点到点之间的变化特征来给出瞬时频率值.因此,局域波法从概念上及信号分析本质上都打破了传统频率的思想,给出了瞬时频率的概念,应该说是整个信号分析领域的重大突破,对非平稳性信号的分析表现出了极大的优越性,并在病理研究、地震波分析及设备的故障诊断中已取得了初步的应用成果.文献 [2]用此方法来分析心、肺和胃部信号,在病理研究上取得了理想的效果;文献 [3]利用 EMD算法对地震波信号进行分析,应用色散曲线揭示了地震波的内涵信息;文献 [4]利用局域波的时频谱对齿轮磨损故障进行了诊断,取得了较好的效果;文献[5]提出了局域波关联维数的故障诊断方法,并利用局域波分析了转子系统各种故障的时频特征;文献 [6]在局域波分解局部能量特征的基础上结合神经网络和粗糙集方法,对柴油机缸套活塞磨损故障进行了诊断;文献 [7]研究了局域波分析与小波分析、Wingner-ville时频分布的区别;文献 [8-9]研究了 EMD方法基于 AR模型预测的数据延拓及端点效应问题;文献 [10]基于阶次跟踪和经验模态分解的滚动轴承包络解调分析.诸多实例的应用结果表明局域波方法非常适于分析非线性非平稳信号.

近似熵是一个用非负数表示某时间序列复杂性及产生新模式的概率的参数[11].近似熵值的大小和采样序列的复杂程度成正比关系,序列越复杂,对应的近似熵值也就越大;当机械设备出现故障时,其振动信号往往呈现出不同程度的不规则性和复杂性,因此通过提取相应运行状况下的复杂性测度(近似熵)[12-13],可以作为设备运行状况的状态特征量.信号中的噪声成分主要分布在高频段,而局域波分解也是从高频到低频的分解,所以信号中的噪声成分也主要集中在前几个分量中,并且白噪声与任何信号都不相关[14],即白噪声与任何信号的互相关系数近似为零,而齿轮减速器中的滚动轴承故障特征频率在低频段,如果在低频段处能够找到较大的相关性,那么此低频段一定包含被分析对象的主要信息.

为工程实践服务是任何一种理论和方法的研究的最高目标,也是人们从事科学研究的最终目的.局域波法将表面振动信号分解成具有特定意义的内禀模式分量(IMF),利用实测不同工况下信号的复杂性测度近似熵及局域波分解所得到的趋势项的发展趋势快速区分正常与故障状态,根据相关性参数的变化特点寻求滚动轴承的故障信号主导模态分量,通过对信号主导模态分量的分析,提取故障特征频率,从而准确定位故障源.因此,本文提出基于局域波及相关分析的滚动轴承故障诊断方法,有望获得满意的结果.

1 局域波及相关分析法

1.1 局域波分解的原理

局域波法是基于信号局部特征的自适应时变滤波分解算法,对于一个复杂的非平稳性信号,任一时刻都可能包含多个振荡模式,因此信号在某一时刻会有多个瞬时频率,为了计算瞬时频率[15],需要将信号分解为满足以下条件的内禀模式 (IMF)分量:

1)极值点的数量与过零点数量相等或最多相差一个;

2)在任意时刻,由局部极值点形成的包络线均值为零.

原始数据 x(t)经局域波分解后可以表示成式(1)

式中:Ci为第 i个 IMF分量;Rn为趋势项.

局域波分解过程就是把信号分解成多个 IMF分量和一个趋势项的和.各模式分量的频率随着分解阶数的增大而降低,趋势项则是频率最低的成分,此结果与小波分解类似,但是小波分解不具备自适应的特点,基本小波一旦被选定就必须用来分析全部数据,因此完全有可能在全局上最优的小波基,在局部上表现得则非常差,并且不同的小波基的分析结果不存在量上的可比性,这两方面的影响制约了小波变换的工程应用.而局域波分解的基函数则是根据被处理信号自适应产生,因此具有良好的信号局部表征能力.

1.2 相关分析

白噪声与任何信号不相关,因此理想的白噪声与原信号的互相关系数为零.由于噪声信号在局域波分解过程中进行了强迫对称分解,己不再是理想的白噪声,所以与原信号的互相关系数不为零,但值相对较小.利用公式(2)计算各 IMF分量与原信号的互相关系数

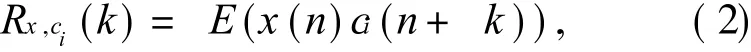
式中:x(n)为原始信号;ci(n)为第 i个局域波分解分量.

如果某基本 IMF分量与原信号的互相关系数值 Rx,ci(k)较小,则此分量有可能为噪声成分.研究各分量与原始信号相关性参数的变化规律,有望准确确定信号主导模态分量.

2 局域波及相关分析法的诊断原理

对滚动轴承而言,某些故障具有一定的敏感频带,当故障发生时该频带内的振动信号会发生较大的变化,因此期望通过比较机械设备在不同运行状态下近似熵的变化及在特征频带内提取对应部件的故障特征频率,有效地监测故障的发生和发展,并做出长期运行趋势的预测,当故障发生时能够准确定位.基于局域波及相关分析的滚动轴承故障诊断方法如图1所示.

诊断步骤如下:

1)测取滚动轴承在不同工况下(正常、故障)的振动信号作为待处理的数据样本;

2)对测得的振动信号进行局域波分解,提取包含主要振源信息的 K个 IMF分量进行分析.本文采用基于信号局部特征的自适应时变滤波分解方法.加速了分解过程,并且局部均值的选取不是基于局部极值的包络均值,而是在局部极值的基础上,通过自适应时变滤波算法得来的,因而更加准确,并且减少了每次分解的迭代次数,得到了更高的分解精度.

3)计算原始信号及每个 IMF分量的近似熵,联合局域波分解所得的趋势项分析和量化的近似熵值,可以判定运行工况是否正常.

4)计算每个分量与原始信号的相关性参数,选择相关性参数发生跃变处的分量或发生跃变处的前后分量作为特征频带,进行功率谱密度分析,提取故障部件的特征频率,准确故障定位.

3 局域波相关分析法的实验研究

3.1 实验研究

本文以齿轮减速器 JZQ250为评测对象(如图2所示),输入轴及中间轴两端的轴承型号均为6406,输出轴两端的轴承型号为 6312,测取其输入轴的输入转速为 1 020 r/min,采样频率为8 000 Hz的正常中间轴上的 5测点处的轴承故障(包括轴承内圈、外圈、保持架故障)工况下的振动信号,在数据预处理的基础上,进行局域波分解,其结果如图3所示.

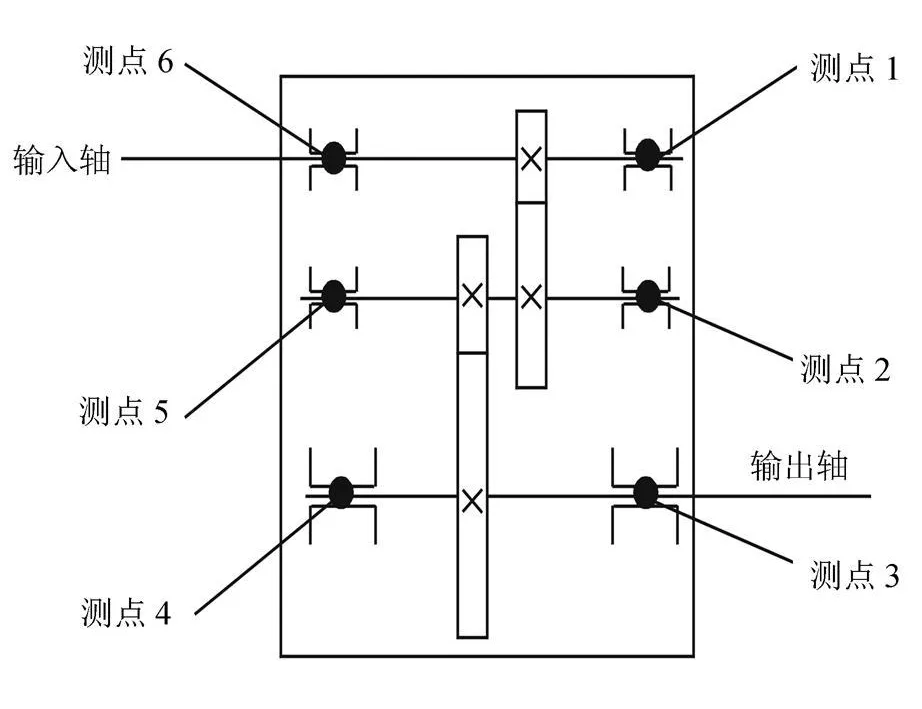
图2 齿轮减速器传动简图Fig.2 Transmission diagram of gear reducer

图3 不同工况下的局域波分解Fig.3 Local wave decomposition at different working conditions

3.2 运行状态趋势分析

当齿轮减速器运行在故障工况下时,其振动信号往往呈现出不同程度的不规则性和复杂性,近似熵作为信号复杂性测度的一个重要指标,可以作为设备运行状况的状态特征量.因此,对不同工况下实测的原始信号进行了近似熵参数的提取,其结果见表1中“原始信号”一列.

从表1中可以看出,故障信号的近似熵较无故障时明显增大,根据近似熵表达时间序列复杂性的特点,可得出在正常工况下测得的信号复杂程度最低,产生新模式的概率也最小,内圈故障工况下信号的复杂程度最高,产生新模式的概率也加大.外圈故障及保持架故障则介于二者之间,借助近似熵可以快速分析信号的复杂性,并且与理论分析结果一致.

为了进一步挖掘有用信息,揭示局域波分解的滤波特性,对局域波分解所得到的各分量也进行了近似熵参数的提取(见表1),各分量的近似熵随着分量阶数的增加而减小,即局域波分解各分量的波形随着分量阶数的增加而趋于规则,与局域波分解的滤波特性完全符合.

众所周知,局域波分解中信号中的最低频部分即信号分解中的最后一层代表了信号的发展趋势,由图3可以明确获知.正常运行状态和故障运行状态下信号的发展趋势截然不同,正常工况下其发展趋势是单调下降的,而在故障工况下则是非单调的,主要表现为上升趋势.把趋势项分析和近似熵相结合,可以更准确地判定其运行状态是否正常,当判定为故障运行状态时,对故障部位的准确定位这一难题又摆在眼前.

表1 原始信号及其局域波分解分量的近似熵Tab.1 Original signal and approximate entropy of local wave decomposition

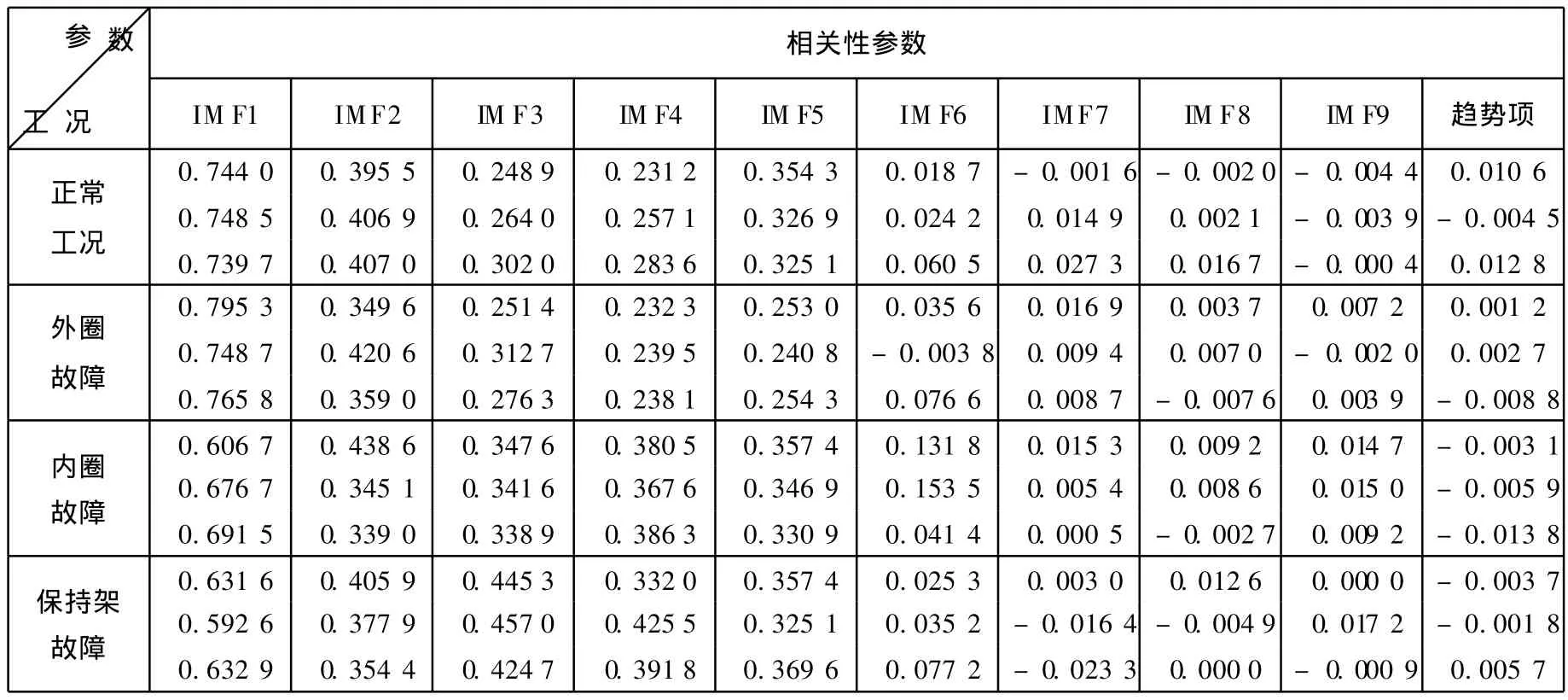
表2 局域波分解分量与原始信号的相关性参数Tab.2 Correlation parameter of local wave decomposition components and original singal

3.3 故障的准确定位

为了对滚动轴承故障部位准确定位,寻求与故障部位一一对应的特征参量,总结下来对于滚动轴承最恰当的仍然是在特定工况下各部件的特征频率,于是对各分量与原始信号的相关性参数进行求解,如表2所示.从相关性参数表的第一列来看,各种工况下分量1与原始信号的相关性最大.

正常、外圈故障工况下分量1～4的相关性依次递减,到分量 5处发生跃变,相关性有所增加,并且正常工况下的增长幅度明显比外圈故障工况下的增长幅度要大的多,分量6～9相关性参数总体呈下降趋势;内圈故障工况下,分量1～ 3相关性依次递减且变化幅度基本稳定,到分量4处发生跃变,相关性有所增加,之后又呈下降的趋势;保持架故障工况下前两个分量的相关性逐渐减弱,到分量 3处有所增加,3～7分量的相关性参数总体呈下降趋势,到分量 8时又有所增加.

通过以上分析,提取相关性参数发生跃变的分量处及发生跃变分量的前后分量进行功率谱密度分析,结果发现在外圈故障工况下的分量 5处,内圈故障工况下的分量4处,及保持架故障工况下的分量8处分别提取到了中间轴上5测点处各种故障部位的特征频率(见表3),而在正常工况下分量 5处提取到了 1/4的工频频率,如图4所示.以上结果是通过大量实测数据的处理而得出的,凝练出了信号主导模态分量的提取方法,有一定的实用价值.

以上判定结果和预知的故障类型一致,说明利用这种方法进行滚动轴承故障信号主导模态分量的确定切实有效.

表3 JZQ250型传动箱轴承故障特征频率Tab.3 Fault feature frequency of rolling bearingsin JZQ250

图4 不同工况下特征频带的功率谱密度Fig.4 Power spectral density of characteristic frequency band in different working conditons

4 结 论

1)在局域波分解的基础上,利用趋势项的发展趋势分析可以快速有效地区分正常和故障工况;

2)利用量化后的特征参量近似熵值能够判别分析信号的复杂性及产生新模式的概率,联合趋势项的发展趋势可以更准确地区分正常工况和故障工况;

3)根据各分量相关性参数在不同分量处发生跃变的特性,有效提取信号主导模态分量,继而提取各种工况下的特征频率,准确定位故障部位.

本文提出了基于局域波分解与相关性参数相结合的滚动轴承故障诊断方法.实例验证表明:该方法可以有效提取不同故障部位的特征频率,并且有效地进行故障定位.该诊断方法对不同类型的齿轮减速器轴承的故障诊断及维修保养提供了新的思路.

[1]马孝江,余泊 ,张志新,等.一种新的时频分析方法-局域波法[J].振动工程学报,2000,13(5):219-224.Ma Xiaojiang,Yu Bo,Zhang Zhixin.et al.A new method to time-f requency analysis-local wave[J].Journal of Vibration Engineering,2000,13(5):219-224.(in Chinese)

[2]Baloeehi R,Menieucci D,Santareangelo E,et al.Deriving the respiratory sinus arrhythmia f rom the heartbeat time series using empirical mode decomposition[J]. Chaos,Solitons and Fraetals,2004,20(1):171-177.

[3]Zhang R,Ma S,Hartzell S.Signatures of the seismic source in EMD-based charaeterization of the 1994 Northridge,California,earthquake recordings[J].Bulletin of the Seismological Society of Ameriea,2003,93(1):501-518.

[4]Flandrin P,Rifling G,Goncalves P.On empirical modedecomposition as a filter bank[J].IEEE Signal Processing Lett.,2004,11(2):112-114.

[5]王凤利,马孝江.基于局域波时频分析的齿轮故障诊断[J].农业机械学报,2006,37(l2):221-225.Wang Fengli,Ma Xiaojiang.The gear fault diagnosis based on local wave time-frequency analysis[J].Transactions of the Chinese Society for Agricultural Machinery,2006,37(l2):221-225.(in Chinese)

[6]王奉涛,马孝江.基于局域波-粗糙集-神经网络的故障诊断方法研究[J].内燃机工程,2007,28(2):80-84.Wang Fengtao,Ma Xiaojiang. Research on fault diagnosis method based on local wave method-rough sets theory-NN[J]. Chinese Internal Combustion Engine Engineering, 2007, 28(2): 80-84. (in Chinese)

[7]向玲,唐贵基.旋转机械非平稳振动信号的时频分析比较[J].振动与冲击,2010,29(2):42-45.Xiang Ling,Tang Guiji.Vibration signal's timefrequency analysis and comparison for a rotating machinery[J].Journal of Vibration and Shock,2010,29(2):42-45.(in Chinese)

[8]胡劲松,杨世锡.EMD方法基于 AR模型预测的数据延拓与应用 [J].振动、测试与诊断,2007,27(2):116-120.Hu Jingsong,Yang Shixi.ARmodel prediction-based EMD method and its application to data extension[J].Journal of Vibration,Measurement& Diagnosis.2007,27(2):116-120.(in Chinese)

[9]杜修力,何立志.经验模态分解(EMD)中边界处理的新方法 [J].北京工业大学学报,2009,35(5):626-632.Du Xiuli,He Lizhi.A new method of processing the boundary problem in the empirical mode decomposition(EMD) [J]. Journal of Beijing University of Technology,2009,35(5):626-632.(in Chinese)

[10]康海英,栾军英,郑海起.等.基于阶次跟踪和经验模态分解的滚动轴承包络解调分析 [J].机械工程学报,2007,43(8):119-123.Kang Haiying,Luan Junying,Zheng Haiqi,et al.Envelope demodulation analysis of bearing based on order tracking and empirical mode decomposition[J].Chinese Journal of Mechanical Engineering,2007,43(8):119-123.(in Chinese)

[11]Flandrin P,Rifling G,Goncalves P.On empirical modedecomposition as a filter bank[J].IEEE Signal Processing Lett,2004,11(2):112-114.

[12]林丽,赵德有.基于局域波近似熵的声发射信号处理[J].大连理工大学学报,2010,50(1):75-80.Lin Li, Zhao Deyou. Acoustic emission signal processing based on local wave and approximate entropy [J]. Journal of Dalian University of Technology,2010,50(1):75-80.(in Chinese)

[13]栗然,陆凤怡.基于局域波与近似熵的负荷分析方法[J].中国电机工程学报,2010,30(25):50-58.Li Ran,Lu fengyi.Novel approach for load analysis based on local wave and approximate entropy[J].Proceedings of the CSEE,2010,30(25):50-58.(in Chinese)

[14]胡红英,马孝江.基于局域波分解的信号降噪算法[J].农业机械学报,2006,37(1):118-120.Hu Hongying,Ma Xiaojiang.Signal denoising based on local-wavedecomposing method[J].Transactions of the Chinese Society for Agricultural Machinery,2006,37(1):118-120.(in Chinese)

[15]别锋锋,郭正刚,张志新.基于局域波时频谱的系统级故障诊断方法研究 [J].仪器仪表学报,2008,29(5):1092-1095.Bie Fengfeng, Guo Zhenggang, Zhang Zhixin.Research on system-level fault diagnosis based on local wave time-frequency spectrum[J]. Chinese Journal of Scientific Instrument,2008,29(5):1092-1095.(in Chinese)