两栖武器水上射击运动位移规律仿真计算✳

郭文凤,潘玉田,郭昭蔚

(1.中北大学机电工程学院,山西太原 030051;2.沈阳理工大学装备工程学院,辽宁沈阳 110159;3.中国船舶重工集团第713研究所,河南 郑州 450015)

两栖武器作为抢滩登陆的重要作战武器装备,不仅要具有良好的陆地作战而且要求具备良好的水上性能,更要求其具备优良的水上攻击性能[1].两栖武器在水中实现精确打击是考核两栖武器装备的重要战技指标之一,因此其在水上射击过程中,由后坐和复进引起的位移变化规律是两栖武器系统射击姿态稳定性和命中精度的主要影响因素.由于两栖武器水上射击的资料不甚完善,因此借鉴船载火炮发射系统的多自由度动力学模型,建立两栖轮式自行武器系统的动力学模型,并用数值计算的方法分析其运动和受力规律[2].

本文对不同射角条件下两栖武器水上射击过程中的车体运动过程进行了数值模拟,得到了车体的水上射击位移运动规律,为今后两栖武器系统的结构研究以及水上性能研究提供了一定的参考价值.

1 水上射击动力学模型的建立

1.1 基本假设

两栖武器系统在水上射击时,处于一个流固耦合的状态,运动形式复杂,所受载荷较多而且是与车辆姿态相关的时变系统.而且由于车体的复杂外形,它在任意浮态和运动状态时,水对它的作用力难以确定.因此研究两栖武器水上射击的位移规律,需要在一定的基本假设之上,忽略次要因素,使问题得以简化而更容易研究.基本假设如下:

1)整车位于无限广域的静水中,不考虑波浪对车体运动的影响;

2)车体、火炮后坐部分均为刚体;

3)射击瞬间,车体静止,不存在推力和转弯离心力以及风力的干扰;

4)射击瞬间,车体姿态由静浮时它的质量及外形特性决定;

5)射击过程中,忽略推进装置和操纵装置的影响.

1.2 坐标系的建立

两栖武器水上射击时可简化为一个 7自由度的运动模型,包括车辆的六自由度空间运动与火炮后坐复进运动.要研究两栖武器的运动,必须建立表达车辆运动的参考坐标系,包括惯性坐标系,车体运动坐标系和后坐体固连坐标系这三个坐标系.其中:惯性坐标系 E aZY,E a轴保持水平,以车辆的主航向为 E a轴正方向,E Z与 E a轴处于同一水平面,E Y垂直于 E aZ平面竖直向上.车体运动坐标系 oxyz,坐标系原点 o选在车体内部某一点,ox轴正向指向车首方向,平行于水线面[3-4];oy轴垂直于 ox轴平行于水线面,以指向车辆右舷为正;oz轴垂直于oxy平面以向上为正.后坐运动坐标系 o′x′y′z′,坐标系原点 o′选在后坐部分内部某一点,o′x′轴正向指向膛口方向,平行于炮膛轴线;o′y′轴垂直于 o′x′轴平行于水平面 ,以指向身管右侧为正;o′z′轴垂直于 o′x′y′平面以向上为正.两栖武器水上运动参考坐标系如图1所示.

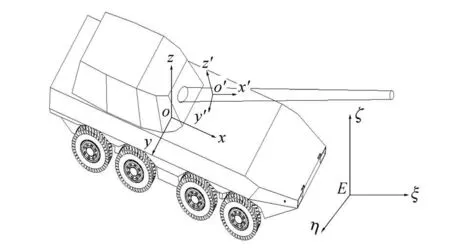
图1 两栖武器水上运动参考坐标系Fig.1 Reference frame of amphibious weapon’s locomotion on water

1.3 车体受力分析

两栖武器在水上射击过程中的运动涉及复杂的流体力学问题,必须将其合理简化.将流体的作用力分为流体静作用力(浮力)与流体动作用力(水动力),前者只与车体位置和姿态有关,而后者不仅与车体位置和姿态有关,还与车体的运动状态有关.除了水对车体产生的浮力和水动力之外,火炮射击对作为射击平台的车体不可避免地会产生一定的影响和冲击.

两栖武器系统在水上射击时车体所受载荷主要有火炮后坐阻力 FR及其对车辆质心的力矩 MR,两栖武器系统的重力 W和车体上作用的浮力 B,车辆上作用的流体水动力,包括流体惯性力和流体黏性力[5].受力分析如图2所示.

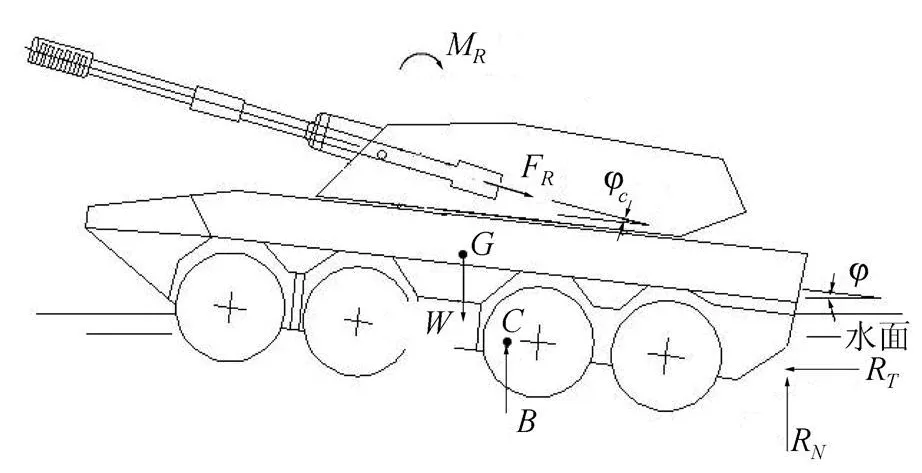
图2 车体水上射击受力图Fig.2 Diagram of force of the amphibious shooting on water

1.4 动力学方程的建立

1.4.1 两栖武器纵中面内静止射击车体动力学平移方程

由于车辆具有左右完全对称性,在火炮射击方向角为 0的情况下,两栖武器仅在车辆纵中面内运动.根据车体的受力分析情况,可建立两栖

武器纵中面射击动力学平移方程,通过对流体惯性力公式进行简化可得到下列方程:

式中:m为两栖车辆运动水上射击时的战斗全重;u为两栖轮式自行火炮的纵倾速度;v为火炮的横倾速度;w为火炮垂直甲板速度;p为纵倾角速度;q为横倾角速度;r为翻转角速度;a为纵向位移量;Z为横向位移量;Y为升沉量;h为横摇角;θ为纵摇角;j为首向角;λ为附加质量;X为纵向力;Y为横向力;Z为垂直甲板力;B为火炮在水中的浮力;w为两栖武器的重力;FR为后坐阻力.

1.4.2 两栖武器系统纵中面内静止射击车体动力学转动方程

根据动量矩定理可知,刚体对原点动量矩的绝对变化率(惯性坐标系下的变化率)等于该瞬时其所受外力的合力对原点的矩,=TE,L为刚体对原点的动量矩;TE为外力合力对原点的力矩.两栖武器对坐标系原点的动量矩为

对于刚体,W R G/W t=0,则车体水上运动一般方程的转动方程

式中:RG为两栖武器质心 G在运动坐标系下的位置向量;Ω为车体转动角速度;J为两栖武器对原点的惯量矩阵;U为车体运动坐标系原点的速度.写成矩阵的形式为

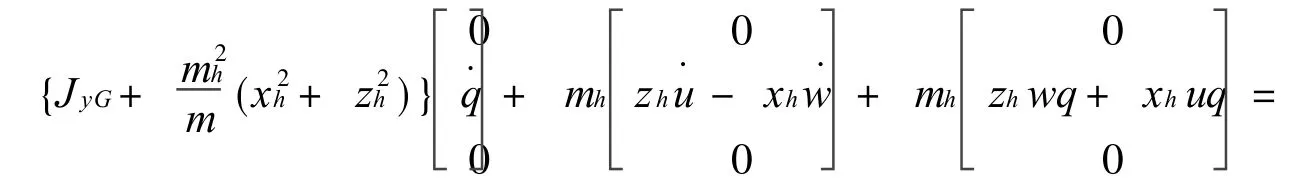
式中:K为横倾力矩;M为纵倾力矩;N为偏航力矩;xh,yh,zh是和火炮方向角jc,高低角hc相关的时变函数.

1.4.3 两栖武器系统后坐复进运动方程

根据火炮射击理论[6],在车体运动坐标系中考察火炮的后坐复进运动,因为火炮后坐复进运动是一个连续的过程,其后坐复进速度在后坐部分运动坐标系中可同一表示

式中:Fhf为后坐和复进的合力;mh为火炮后坐部分质量;Uhf为后坐部分质心速度[7].

1.4.4 绝对速度与绝对位移

在进行惯性坐标系和车体运动坐标系之间的坐标轴转换时,曾三次绕轴旋转完成,并把绕三轴的转角分别记为j,θ,h,所以绕三轴的角速度可分别用 j˙,θ˙,h˙表示 .根据假设条件 h=j=0,参考船舶建立船舶姿态运动学方程的方法[8],可获得两栖武器水上射击时的姿态运动学方程

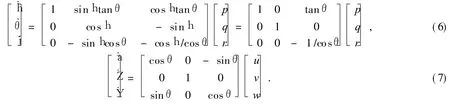
将式(2)和(4)～ (7)联立即为两栖武器水上射击动力学方程组,共包含车辆进退、升沉、纵摇、火炮后坐运动 4个方向的运动,作用在车辆上的载荷包括 7自由度两栖武器水上射击动力学方程中所有的载荷.

2 数值仿真

在进行水上射击动力学方程组数值求解的过程中,需要计算两栖武器系统的水上姿态的基本参数.通过改变车体在水中的的升沉量Y和姿态角(横摇角h,纵摇角θ),即可求得每个时刻对应一个车辆的位置与姿态.而与车辆位置与姿态对应的浮力值与浮心位置,可通过插值或者拟合的方法获得车体的运动位移的规律.本文以两栖轮式自行火炮为例,通过 VB编程进行了Solidworks二次开发[9-10],获得了车辆静浮状态的水线面位置和静浮状态时的浮心位置,可作为动力学方程求解时的初始条件[11].

1)车辆初始运动参数与状态参数

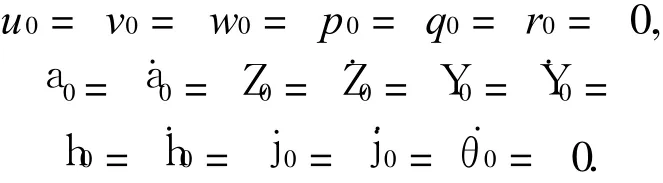
2)车体运动坐标系中初始后坐部分质心位置

工况 1.当高低角为 0°时,(xh0,yh0,zh0)=(438.35,0,848.16);

工况 2.当高低角为 45°时,(xh0,yh0,zh0)=(180.34,0,1655.04);

工况 3.当高低角为 70°时,(xh0,yh0,zh0)=(-200,0,1945.18).

3)火炮全重 m=20 t,后坐部分质量 mh=1.13 t,初始纵倾角 θ0=0.87°,射击方向角j c=0°.

本文利用 Matlab软件对炮身有后坐阻力的运动过程及后坐结束后的炮身运动过程的位移变化进行了数值仿真计算[12-13],积分方法与步长由MATLAB内部函数 ode45确定,并采用分段的计算方法,在火炮运动开始初期采用较小的时间步长进行计算,当火炮后坐结束后,采用较大的时间步长计算自由运动阶段的位移过程.图3,图4分别所示的是射角为 70°时后坐纵向位移和垂向位移变化的曲线图.表1为该两栖轮式自行火炮不同射角条件下水上射击位移量及纵倾角位移的计算结果对比.

图3 射角为 70°时后坐纵向位移随时间变化曲线Fig.3 Varation curves of recoil longitudinal displacement with time,the angle of 70°

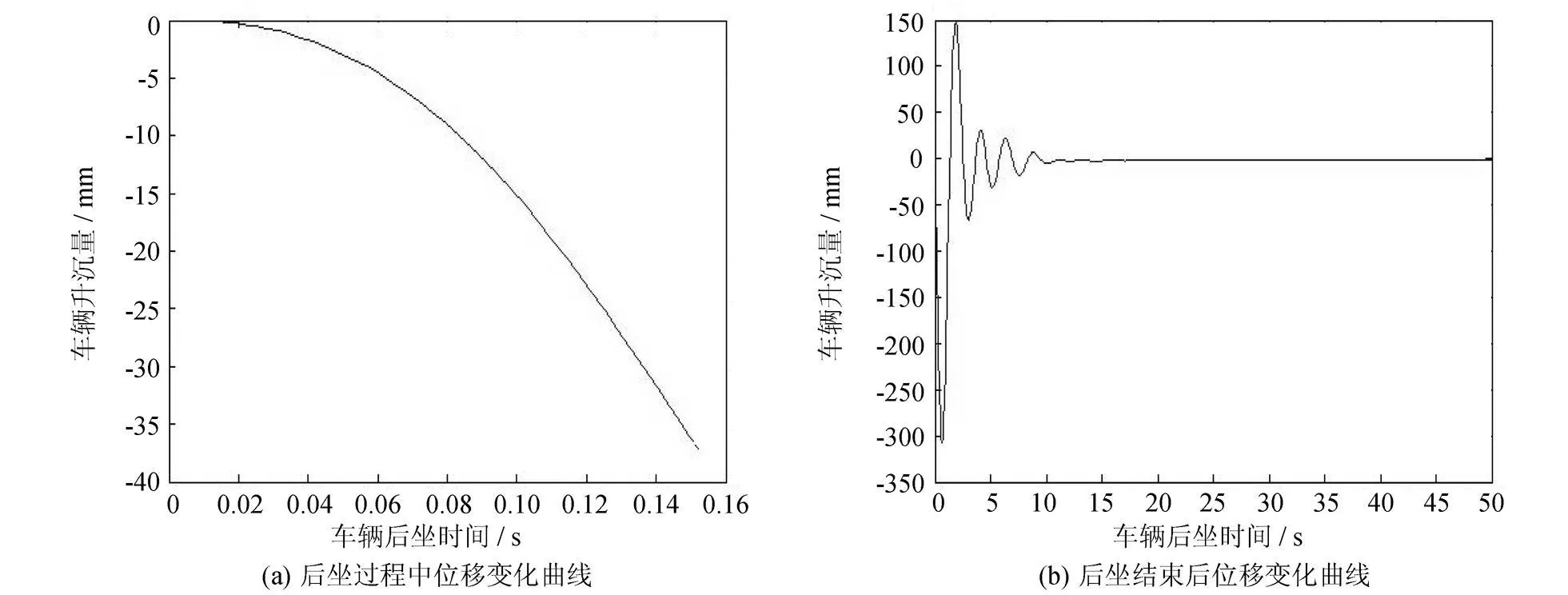
图4 射角为 70°时后坐垂向位移随时间变化曲线Fig.4 Varation curv es of recoil vertical displacement with time,the angle of 70°

表1 两栖轮式自行火炮水上射击位移计算结果Tab.1 The calculation result of the amphibious weapon shooting on water

3 结果分析

计算结果表明两栖轮式自行武器在水上射击时射角的大小对两栖轮式装甲车辆射击后的位移大小有较大的影响.从表1中可知,当射角h c=0°时,纵向位移最小值为 4.878 m,垂向位移最大值为 72.5 mm;当射角 h c=70°时,纵向位移最小值为 1.54 m,垂向位移最大值为 147 mm.表明火炮射角越大,车体的纵向位移越小;而垂向位移越大,纵倾角度越小.这是由于射角达到 70°时的火炮后坐阻力最大值比其他两个工况下的后坐阻力值大,加之有水动力的影响,因此车体的升沉量会增大.

目前,实车射击的资料比较缺乏,但是根据两栖车辆模型冲击载荷试验[14]资料数据对比发现,数值仿真与模型试验结果所表现的位移变化规律是基本趋于一致的.本文通过数值仿真模拟计算了两栖武器水上射击运动位移规律,对研究其水上射击性能具有一定的实际意义.由于两栖车辆在进行实际水上射击时的影响因素过多,因此可以在本文的基础上进行进一步深入的研究.

[1]杨楚全.水陆两栖车辆原理与设计 [M].北京:国防工业出版社,2005.

[2]杨国来.船载火炮系统的运动稳定性研究[J].南京理工大学学报,1999,23(3):205-208.Yang Guolai. Study on kinetic stability of trawler system with howitzer[J]. Journal of Nanjing University of Scienceand Techonology,1999,23(3):205-208.(in Chinese)

[3]郭保全 .CAD二次开发进行两栖装甲车水上性能分析[J].华北工学院学报,2003,24(3):170-173.Guo Baoquan. Analysis of the waterborne performance of amphibious armored vehicles with CAD secondary developing[J].Journal of North China Institute of Technology,2003,24(3): 170-173(in Chinese)

[4]侯宏花.CAD二次开发与两栖车辆水上性能分析 [J].机械管理开发,2005(3):89-90.Hou Honghua.Analysis of the waterbore capability of amphibious armored vehicles with CAD secondary developing [J]. Mechanical Management and Development,2005(3):89-90.(in Chinese)

[5]潘玉田,谌勇.一种轮式自行火炮水上射击动力学分析的方法[J].火炮发射与控制学报,2002(2):29-33.Pan Yutian,Chen Yong.A method of the aquatic shooting dynamics analyses of wheeled self-propelled guns[J].Gun Launch& Control Journal,2002(2):29-33.(in Chinese)

[6]高树滋.火炮反后坐装置设计[M].北京:兵器工业出版社,1995.

[7]李美彦.两栖武器水上射击后坐运动规律研究[J].舰船科学技术,2010,32(11):26-29.Li Meiyan.Study of recoil force rule of amphibious weapon shooting on water[J]. Ship Science and Technology,2010,32(11):26-29.(in Chinese)

[8]李殿璞.船舶运动与建模 [M].哈尔滨:哈尔滨工程大学出版社,1999.

[9]张树兵,戴红,陈哲.Visual Basic 6.0中文版入门与提高[M].北京:清华大学出版社,1999.

[10]江洪,李仲兴,邢启恩.Solidworks 2003二次开发基础与实例教程 [M].北京:电子工业出版社,2003.

[11]李美彦,郭保全.基于 Solidworks二次开发的两栖武器浮心与浮态计算方法 [J].火炮发射与控制学报,2010(3):66-69.Li Meiyan,Guo Baoquan.Computational method on buoyancy center and floating state of amphibian weapons based on solidwords secondary development[J].Journal of Gun Launch& Control,2010(3):66-69.(in Chinese)

[12]张圣勤.MATLAB 7.0使用教程 [M].北京:机械工业出版社,2006.

[13]刘卫国.MATLAB程序设计与应用[M].北京:高等教育出版社,2006.

[14]潘玉田,侯红花,郭张霞.现代火炮系统测试技术[M].北京:兵器工业出版社,2011.