催泪子母弹合理开仓时间研究✳

吴占文,彭维仕,邹 南,丁 成,刘文瑶

(1.武警工程大学基础部,陕西西安 710086;2.武警工程大学装备运输系,陕西西安 710086)

催泪子母弹(如图1所示)为公安与武警部队反恐处突维稳武器装备防暴弹发射器配属防暴弹药,弹体落地后以其战斗部装填的催泪剂驱散闹事人群.催泪子母弹开仓时间由延期管控制,约为 5 s[1].实弹发射表明:发射角较大时,子弹分离母弹后,会出现空中起烟;发射角较小时,又不能在空中及时开仓.这两种情况都会影响催泪效应.本文在阐明催泪子母弹的结构组成及其开仓原理的基础上,拟运用 MATLAB/Simulink仿真软件对其在不同发射角时的外弹道曲线进行模拟仿真,获得了子母弹在不同发射角时的弹道曲线、开仓高度;结合实弹数据和仿真结果,着重分析了子弹分离后的起烟情况及其对人群的作用效应.通过改变药柱起烟时间及利用加权平均方法,优化该子母弹开仓时间,使其在不同发射角时既保证非致命性,又达到较强的催泪效应,以期提高催泪子母弹的作战效能.

图1 催泪子母弹Fig.1 Multiple tear bomb

1 催泪子母弹结构组成及开仓原理

催泪弹主要由上垫、母弹壳体、药盒、延期管、弹托、高低压室、底火等组成.发射器通过电击发引燃火帽,火帽引燃高压室内发射药.发射药燃烧产生气体,达到一定压力后,火药气体冲破高压室中的塑料薄膜进入低压室,推动母弹运动的同时使弹底和弹托分离,并点燃延期点火管.母弹射出后约 5 s,延期点火管点燃开仓点火药,瞬时产生高温高压气体膨胀做功,推动上垫,使弹壳向前,同时推弹托向后,破坏母弹壳体与弹托扣合的螺纹力,使两者分别向前和向后加速飞行,实现分离[2].

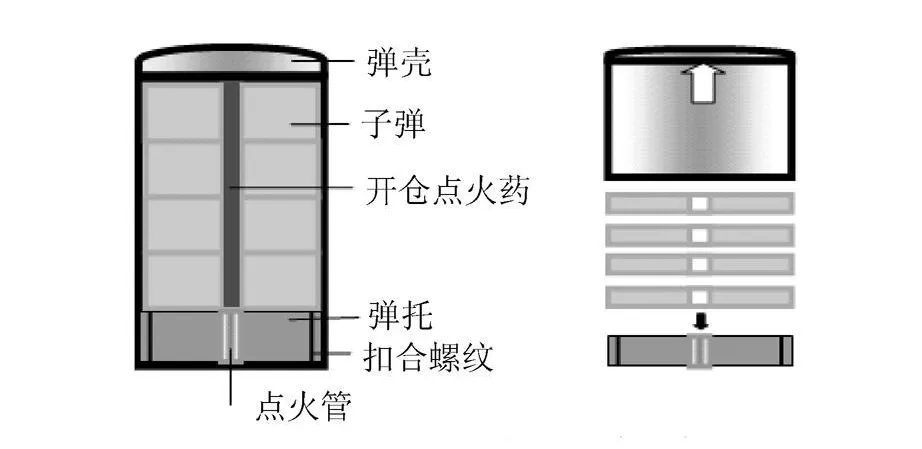
图2 催泪子母弹开仓示意图Fig.2 Rupture chart of multiple tear bomb

螺纹断裂后,弹内剩余气体继续作用于弹壳和子弹,使两者向相反方向运动,实现开仓,将子弹抛撒出去(如图2所示);子弹抛射后,点火药点燃药柱发烟,构成多点投放,在一定的抛撒范围内形成发烟效果.

2 催泪子母弹外弹道模拟仿真

外弹道学是研究弹丸在空中的运动规律以及与此运动有关的问题[3].弹丸在空中的运动规律一般用一阶微分方程组描述,少数微分方程能用初等方法求得解析解,多数问题需要借助于现代仿真技术来解决.目前,外弹道仿真算法常采用直线法,定点抛物线法,解质点弹道方程组,解刚体弹道方程组等[4-5].本文拟采用解质点弹道方程组的方法,根据文献[1]提供的催泪子母弹外弹道数学模型,运用 MATLAB/Simulink仿真软件对其进行外弹道模拟仿真;然后将仿真结果与该子母弹弹道性能试验数据作比较分析,以期验证仿真结果,为优化该子母弹的开仓时间奠定基础.

2.1 基本假设

催泪子母弹空中飞行情况复杂,若考虑全部因素会使求解困难,因此作如下基本假设:①地球表面为平面;②重力加速度大小和方向不变,科氏加速度为零;③整个弹运动期间,章动角为零;④弹丸是轴对称体;⑤ 气象条件是标准的、无风雨[6-10].

2.2 基本外弹道方程

根据文献[1]与[6],得催泪子母弹简化的外弹道方程组

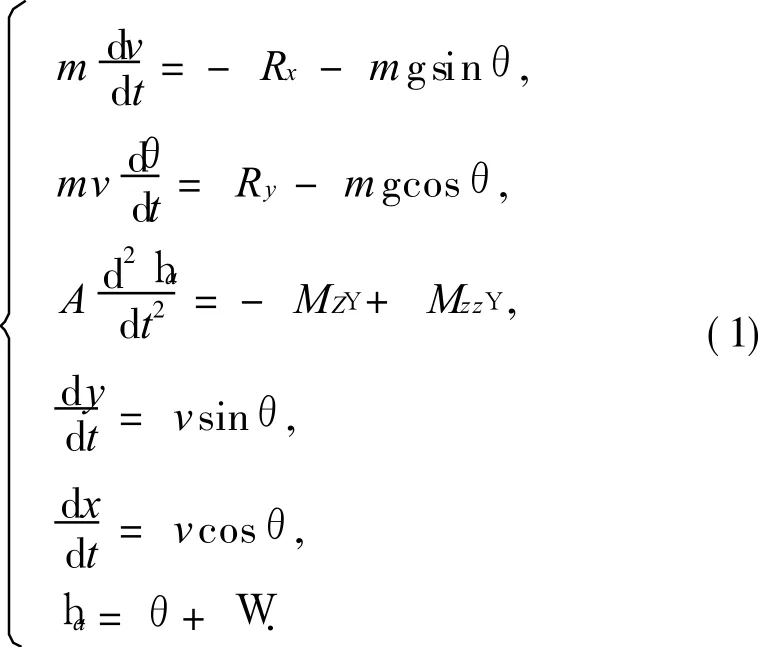
式中:v为弹丸速度,m/s;Rx为阻力,N;m为弹丸质量,kg;g为重加速度,m/s2;t为弹丸运动时间,s;Ry为升力,N;Mz Y,Mzz Y分别为静力矩和赤道阻尼力矩,N·m;A为赤道转动惯量,kg·m2;y为弹丸射高,m;x为弹丸水平射程,m;θ,W分别为弹道倾角和章动角.

积分初始条件:t0= 0,x0=y0= 0,v0=95 m/s,m=0.37 kg,初始射角为 15°,30°,45°,60°.

2.3 仿真实现

由经典外弹道理论可知,当初速度、射角、弹道系数一定时,就可以唯一地确定一条弹道曲线.在进行弹道仿真时,弹道系数可直接在模型中设定,初速度、射角可在相应的积分模块中设定和修改.在进行仿真时,采用变步长的 ode45算法进行仿真,最小步长自动调节,相对误差允许范围为 10-3,绝对误差范围自动调节,从 0时刻开始仿真,设置各个模块的参数后,即可开始仿真.

运用 MATLAB/Simulink仿真软件编写程序[11-16],仿真结果如图 3所示.

图3 不同射角催泪子母弹射高与时间曲线Fig.3 Altitude curve of multiple tear bomb at different launch-angle

2.4 仿真结果分析

催泪子母弹的开仓高度须大于 20 m,才能保证子弹落地时不会对人群造成致命性伤害.由图3(a)与 图3(b)可得,在 30°和 45°的弹道曲线上,对应 5 s处的开仓高度分别为 20 m和 64 m,都大于 20 m,能保证子母弹的非致命性.

表1是催泪子母弹弹道性能试验数据.

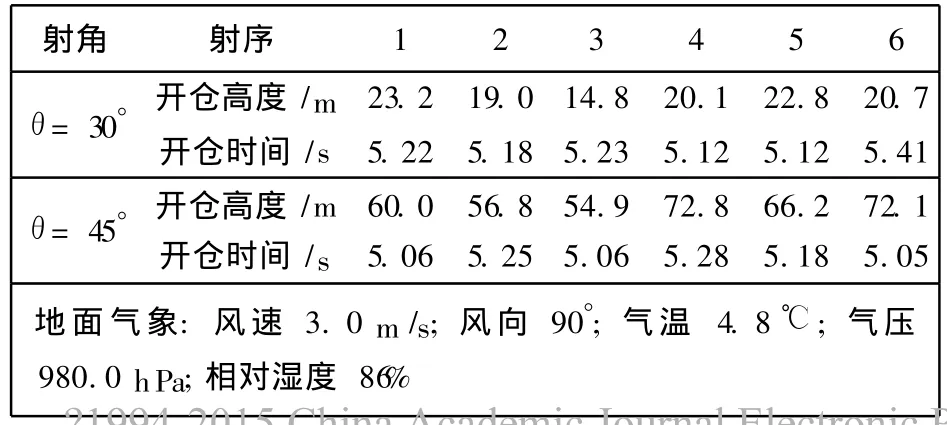
表1 催泪子母弹实验结果Tab.1 Experimental results on multiple tear bomb

由表1可知,射角为 30°时的开仓高度为

同理,射角为 45°时的开仓高度为

将式 (2)与 (3)的计算结果与仿真值作比较分析,可知仿真结果与实际值比较接近.因缺乏射角为 15°和 60°时的实验结果,所以本文基于射角为 30°和 45°仿真时的弹道参数,改变射角,得15°和 60°时的仿真结果,如图3(c)和图3(d)所示.从图3(c)中可知,曲线上对应 5 s处的开仓高度大致为 85 m.根据药柱燃烧特性考虑,药柱起烟时间为 3.5 s[2],用自由落体公式 h=1/2gt2,算出理论开仓抛撒高度为 61.25 m.显然,实际开仓高度大于理论值,即子弹分离母弹后,没有到达地面时就会起烟.根据催泪剂的特性,子弹到达地面后才能发挥最佳催泪效果.可见,射角较大时,催泪弹效果不好,故需延长药柱起烟时间,即增大开仓高度的理论值.但延长药柱起烟时间又会影响射角较小时催泪弹落地后的起烟时间,影响催泪弹的战术效应.所以需综合考虑射角较小时的情况,才能确定较优的药柱起烟时间.从图3(d)中可以看出,射角为 15°时,整弹空中运动时间 ＜5 s,出现子弹未分离就到达地面的情况,而且弹的存速较大,对人群致命性伤害也较大.故需调整弹的开仓时间,使其在安全的开仓高度内(＞20 m).

由上述情况可知,子母弹在发射角较大时,子弹分离母弹后出现空中起烟,发射角较小时又不能在空中及时开仓,这两种情况都会影响催泪效应.因此,子母弹开仓时间不合理,需进行优化设计.

3 开仓时间优化设计

由仿真结果分析可知,催泪弹在 60°角发射时,需延长药柱起烟时间,子弹到达地面后起烟,以发挥最佳催泪效应.经试验和计算,初步确定药柱的起烟时间为 4.0±0.5 s,用自由落体公式h=1/2gt2,算出开仓抛撒高度为 80～ 90 m,与仿真结果相差不大,即满足要求.从图3(d)中可得,射角为 15°时,需缩短开仓时间才能满足要求.本文利用加权平均的方法,取各射角的最佳开仓时间的加权平均,得出一个较合理的开仓时间,再从仿真结果中找出相对应的开仓高度,以验证该时间的合理性.加权平均公式为

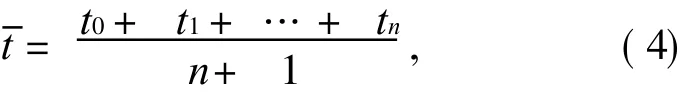
式中:t0,t1,tn分别为各射角的最佳开仓时间.

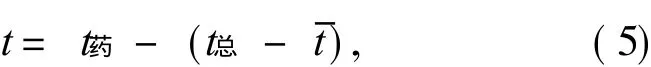
式中:t药为药柱起烟时间;t总为弹的运动总时间.代入数据,计算结果如表2所示.可见,落地后起烟最长的起烟时间为2.0±0.5s,即满足了战术要求.

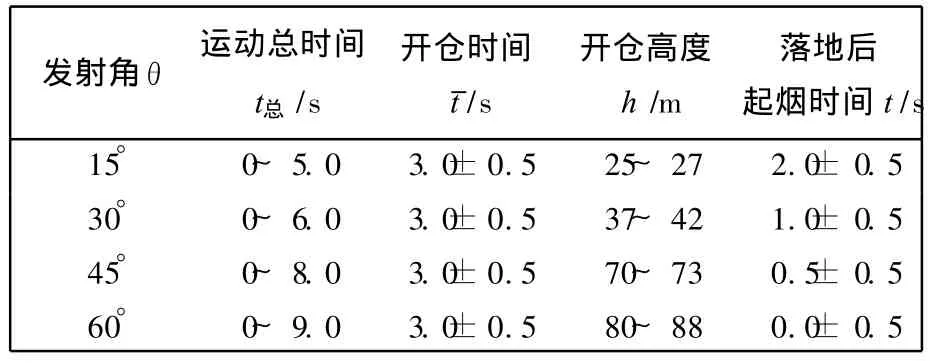
表2 调整后不同发射角催泪子母弹仿真结果Tab.2 Simulation result on multiple tear bomb at different launch-angleafter adjustment

由上述结果可知,理论上催泪子母弹开仓时间定为 3.0±0.5 s是合理的.按设计要求制成新的催泪子母弹进行实弹射击,结果如表3所示.由表3可知,射角为 15°时,开仓高度为

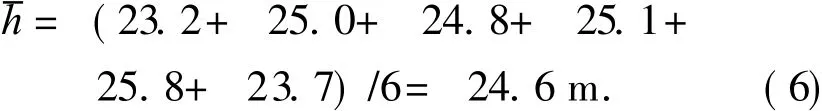
同理,射角为 60°时,开仓高度为

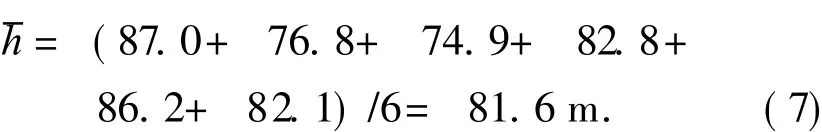
由式 (6)和 (7)知,射角为 15°和 60°时的开仓高度分别为 24.6 m和 81.6 m,都大于 20 m,既能保证催泪弹的非致命性,又能保证子弹在到达地面后适时起烟.由表3可知,射角为 15°时,落地后起烟时间

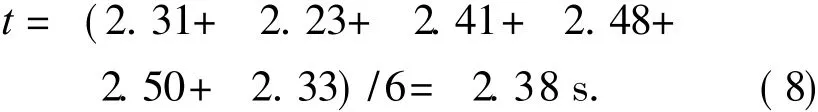
同理,射角为 60°时,落地后起烟时间

由式 (8)和 (9)知,当射角为 15°和 60°时,落地后的起烟时间分别为2.38s和 0.39s,满足战术要求.

表3 催泪子母弹实验结果Tab.3 Experimental results on multiple tear bomb

综上所述,本文将催泪子母弹不同射角下的开仓时间最终统一确定为 3.0±0.5 s,这样既能保证催泪弹的非致命性,又能保证子弹在达到地面后适时起烟,是一个较为合理的开仓时间,优化了催泪子母弹设计,有效地提高了其作战效能.

4 结束语

针对催泪子母弹已定开仓时间不能确保不同发射角发射的非致命性和催泪有效性问题,阐明了催泪子母弹的结构组成及其开仓原理,运用MATLAB/Simulink仿真软件对其进行了外弹道模拟仿真,获得了不同发射角下子母弹的弹道曲线及开仓高度;结合实弹数据和仿真结果,着重分析了子弹分离母弹后的起烟情况及对人群作用的效应.通过改变药柱起烟时间及利用加权平均方法,将催泪子母弹不同射角下的开仓时间统一确定为 3.0±0.5 s这样一个较合理的时间,既保证了催泪弹的非致命性,又能达到较强的催泪效应.优化了催泪子母弹的设计,有效地提高了其作战效能.

[1]韩飞.64 mm催泪弹飞行稳定性研究[D].西安:武警工程学院,2009.

[2]万斌,刘禄胜.64 mm子母弹发烟弹的配比试验 [J].警用技术,2009(4):66-67.Wan Bin,Liu Lusheng.Mixture ratio of 64 mm smoke projectile shell[J].Police Technology,2009(4):66-67.(in Chinese)

[3]王敏忠.炮兵应用外弹道学及仿真 [M].北京:国防工业出版社,2009.

[4]朱敏洁,王精业.实时仿真系统中外弹道仿真的一种方法[J].系统仿真学报,2001,13:303-306.Zhu Minjie,Wang Jingye.A method of trajectory simulation in real time simulation system[J].Journal of System Simulation, 2001, 13: 303-306. (in Chinese)

[5]肖亮,王中原,周位平.外弹道相似理论应用研究[J].弹道学报,2009,21(2):43-46.Xiao Liang, Wang Zhongyuan, Zhou Weiping.Application research on similar theory of exterior ballistics[J].Journal of Ballistics,2009,21(2):43-46.(in Chinese)

[6]韩飞.64 mm催泪弹外弹道数学模型的建立[J].中国科技博览,2010(33):55-56.Han Fei.Theestablishment of mathematical model for exterior trajectory of 64 mm tear shell[J].Science and Technology Review of China,2010(33):55-56.(in Chinese)

[7]杨金柱.64 mm催泪弹的空中运动特性研究[J].武警工程大学学报,2011(1):43-44.Yang Jinzhu.Research on the motion characteristics of 64 mm tear shell in the air[J]. Journal of Engineering University of CAPF,2011(1):43-44.(in Chinese)

[8]杨启仁.子母弹飞行动力学 [M].北京:国防工业出版社,1999.

[9]谷文斌,姚养无,武俊明.某型炮弹外弹道理论分析及数值仿真 [J].机械工程与自动化,2010(4):88-90.Gu Wenbin,Yao Yangwu,Wu Junming.Theoretical analysis and numerical simulation for the exterior ballistic of acannonball[J].Mechanical Engineering&Automation,2010(4):88-90.(in Chinese)

[10]罗雷.子母式催泪弹的设计与研究[D].西安:武警工程学院,2004.

[11]赵法栋,庄弘玮.基于 Matlab/Simulink的防爆动能弹弹道仿真[J].装备制造技术,2009(10):51-53.Zhao Fadong,Zhuang Hongwei.Matlab/simulink based trajectory simulation of aanti-riots kinetic energy munition[J]. Equipment Manufacturing Techology,2009(10):51-53.(in Chinese)

[12]赵军民,何亚娟.基于 MATLAB/Simulink的弹道仿真模块化设计 [J].弹箭与制导学报,2007,27(1):147-153.Zhao Junmin, He Yajuan. The incorporate simulation of the missile trajectory based on MATLAB/Simulink[J]. Journal of Projectiles Rockets Missiles and Guidance,2007,27(1):147-153.(in Chinese)

[13]马利兵,林都.基于 MATLAB的外弹道模型仿真研究[J].中北大学学报(自然科学版),2006,27(5):412-415.Ma Libing,Lin Du.A research on the simulation of exterior trajectory based on Matlab[J].Journal of North University of China (Natural Science Edition),2006,27(5):412-415.(in Chinese)

[14]杨献辉,赵俊利.基于 Matlab的迫击炮外弹道模型仿真研究[J].装备制造技术,2011(2):24-26.Yang Xianhui,Zhao Junli.A simulation research on the external trajectory of mortars based on Matlab[J].Equipment Manufacturing Techology,2011(2):24-26.(in Chinese)

[15]唐克 ,崔卫兵 ,王存威 ,等.基于 Matlab的影响子母弹抛撒精度的因素研究[J].指挥控制与仿真,2010,32(2):59-61.Tang Ke,Cui Weibing,Wang Cunwei,et al.Research on the factor of influencing shrapnel spreading precision based on Matlab[J].Command Control& Simulation,2010,32(2): 59-61. (in Chinese)

[16]梁建波,刘新学.弹道仿真中的数值计算方法研究[J].计算机工程与应用,2009,45(25):231-233.Liang Jianbo, Liu Xinxue. Study on numerical calculation method of ballistic simulation[J].Computer Engineering and Applications,2009,45(25):231-233.(in Chinese)