悬链线的AH Bézier样条表示
2012-10-08李亚娟
李亚娟
(杭州电子科技大学理学院,浙江杭州310018)
0 引言
悬链线是在一条直线上滚动的抛物线的焦点的运动轨迹,发现于300多年前;是微积分、微分方程、微分几何、变分计算及数值分析中的一个重要课题[1-3],被公认为是真实反映实际悬挂钢索的线形,为滑索工程设计提供了科学理论依据[4,5]。由于缺乏必要的精确表达工具,实际中关于悬链线的几何参数与力学参数的相关计算,一般都是通过数值逼近得到的。若能用控制多边形的方法来精确表示悬链线,则能在CAD中发挥其更强大的作用。鉴于悬链线的表达式中既包含一次多项式,又包含双曲正弦函数与双曲余弦函数,因此精确表示悬链线,必须选择多项式混合双曲函数空间的基。考虑利用多项式混合双曲函数空间[6-8]Γn+1=span{1,t,…,tn-2,sinh t,cosh t}的 AH Bézier样条基函数来精确表示悬链线,并给出反求的控制多边形。文献7用均匀代数双曲B样条对悬链线的表示进行了研究,并直接给出4个控制顶点,可以表示一段特殊的悬链线,但是并没有给出如何表示任意一段悬链线的方法。对于任意一段悬链线,本文给出AH Bézier样条基的精确表达式,并给出反求的控制顶点。
1 AH Bézier基函数
先给出AH Bézier基函数的表达式[8]。首先在空间Γ2=span{1,cosh t,sinht}上给定2个初始函数:B0,1(t)=sinh(α -t)/sinh α, B1,1(t)=sinh t/sinh α,t∈[0,α],α >0,α 是形状因子。当 n >1 时,空间Γn+1=span{1,t,…,tn-2,sinh t,cosh t}中的 n 阶 AH Bézier基函数 {B0,n,B1,n,…,Bn,n}可以递推的定义为:

式中,δi,n=1/(t)dt,0<i<n,α是全局形状参数。特别地,给定4个控制顶点pi(i=0,…,3),一条4阶AH Bézier曲线可以定义为:
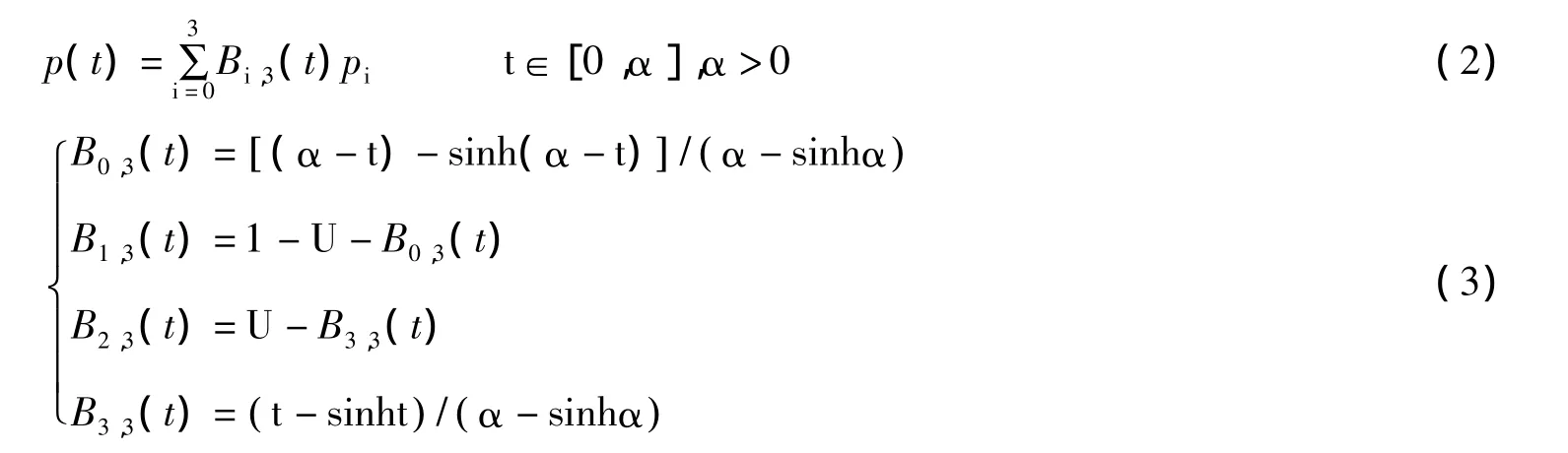
2 悬链线的4阶AH Bézier表示
考察任意一段无荷重悬链线如图1所示。方便起见,选择悬链线的最低点作为原点,重力反方向作为y轴正向,则此段悬链线表达式为:c(u)=(u,a(cosh(u/a)-1)),b<u<c。为了对该悬链线进行精确表示,做线性变换u=(c-b)t/α+b,有:


图1 一条悬链线


根据未知量的个数与基函数的性质,可以断定所求AH Bézier曲线的控制顶点必为唯一一组。由于AH Bézier曲线的首末端点值与切矢值易于计算,有:
对式5两边求导,有:
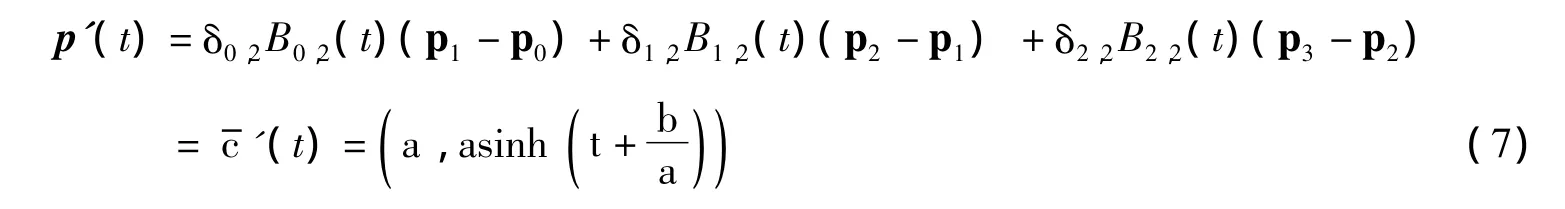
分别令t=0,t=α,得到:

至此,所求4阶AH Bézier曲线的控制顶点均已经求得。如图2、3所示是两段无荷重悬链线用控制多边形表示的例子。以某大跨度悬索桥的参数作为计算资料,中跨跨度为600 m,主塔理论顶点高程均为196.24m,则所求控制多边形如图4所示。

图2 4阶AH Bézier曲线表示下的悬链线
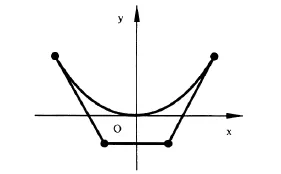
图3 4阶AH Bézier曲线表示下的悬链线

图4 4阶AH Bézier曲线表示下的某大跨度悬索桥
3 结束语
如果不限定形状因子α,可以得到一族悬链线,这族悬链线均具有与原悬链线相同的端点与端点切矢,但是其中只有一条与原悬链线完全重合。在工程设计上可以利用4阶AH Bézier曲线的控制多边形对悬链线进行各种形状控制与高效求值。
[1]Nedev S.The catenary-an ancient problem on the computer screen[J].European Journal of Physics,2000,21(5):451-457.
[2]Juan B Gil.The catenary(almost)everywhere[J].Boletin de la Asociacion Matematica Venezolana,2005,12(2):251-258.
[3]Paul Baginski,Chapman S T ,Ryan Rodriguez,etal.On the Delta set and catenary degree of Krull monoids with infinite cyclic divisor class group[J].Journal of Pure and Applied Algebra,2010,214(8):1 334 -1 339.
[4]Mareno A,Q English L.The stability of the catenary shapes for a hanging cable of unspecified length[J].European Journal of Physics,2009,30(1):97 -108.
[5]Ioannis K Chatjigeorgiou.Application of the WKB method to catenary-shaped slender structures[J].Mathematical and Computer Modelling,2008,48(2):249-257.
[6]Koch P E,Lyche T.Construction of exponential tension B-splines of arbitrary order[C].New York:Academic Press,1991:255-258.
[7]Lü Yonggang,Wang Guozhao,Yang Xunnian.Uniform hyperbolic polynomial B-spline curves[J].Computer Aided Geometric Design,2002,19(6):379-393.
[8]Li Yajuan,Wang Guozhao.Two kinds of B-basis of the algebraic hyperbolic space[J].Journal of Zhejiang University science,2005,6A(7):750-759.
